传送门

 

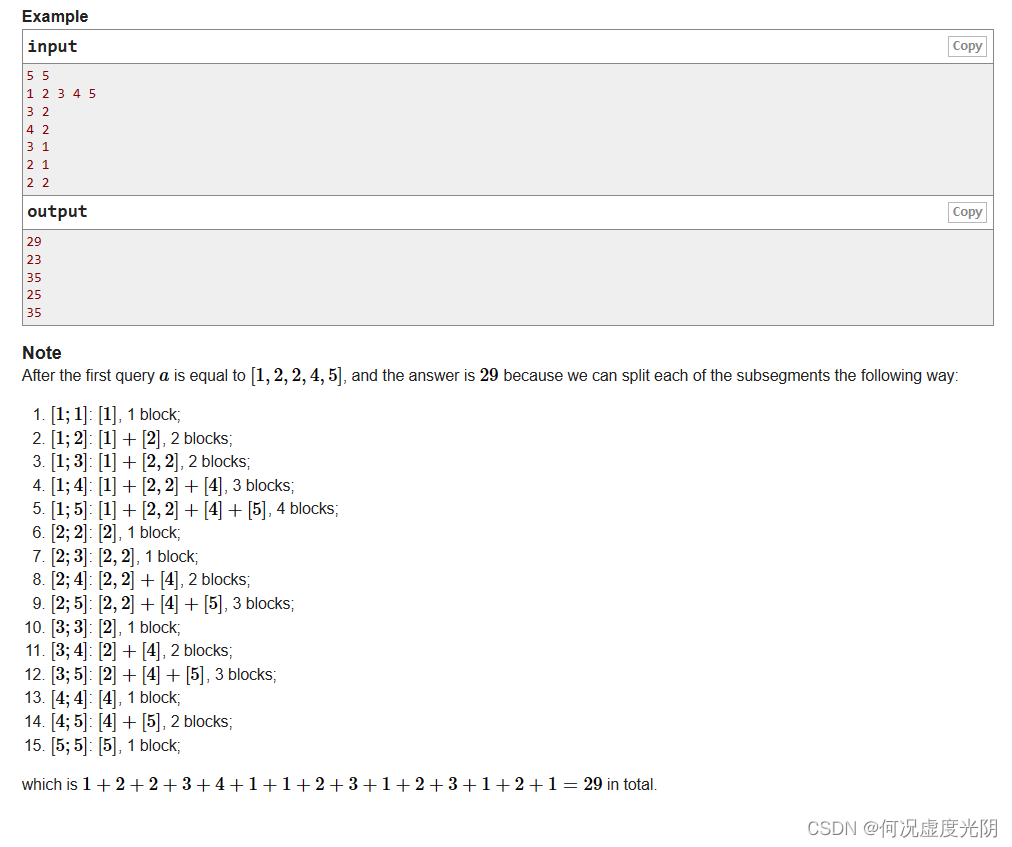
题意：

定义一个数组，定义它 相等连续段的个数
如1,2,2,1，相等连续段有[1],[2,2],[1]，共3个
如2,2,2,1，相等连续段有[2,2,2],[1]，共2个

给定一个数组a，定义g(l,r)为，子数组中a[l],a[l+1],…,a[r]，相等连续段的个数。给定m次操作，每次修改数组第i个位置的值为x。求每次操作后的数组的g函数的值。

f函数定义为： 

 

思路
先来看看全部相等的元素的数组，它的h函数的值。
那么

                 

 

对于一个元素全部相等的区间，它的g函数值为1，
如果修改一个元素，且该元素与其相邻元素不等时，那么该区间的g函数值会加1。

1. 计算初始的h函数值。
我们把数组初始看成n个a[1]。
此时h函数为n*(n+1)/2。

接着把第二个数修改为a[2]，此时，如果a[2]!=a[1]，那么所有包含a[2]和a[1]的区间，g函数都会加1。

这里注意防爆int，转换为long long做计算

AC代码：

#include<bits/stdc++.h>
//#define int long long
using namespace std;
using i64=long long;
const int N=1e6+10;
i64 a[N];
void solve(){
	i64 n,m;
	cin>>n>>m;
	i64 sum=n*(n-1)/2+n;
	for(int i=1;i<=n;i++) cin>>a[i]; 
	for(i64 i=1;i<=n-1;i++){
//		cin>>a[i];
		if(a[i]!=a[i+1]){
			sum+=(i)*(n-i); 
		}
	}
	while(m--){
		i64 i,x;
		cin>>i>>x;
		if(a[i]!=a[i-1]) sum-=(i-1)*(n-(i-1));
		if(a[i]!=a[i+1]) sum-=i*(n-i);
		a[i]=x;
		if(a[i]!=a[i-1]) sum+=(i-1)*(n-(i-1));
		if(a[i]!=a[i+1]) sum+=i*(n-i);
		cout<<sum<<'\n';
	}
	
}
signed main(){
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int t;
//	cin>>t;
	t=1;
	while(t--){
		solve();
	}
}