文章目录
- 说明
- day35 图的 m 着色问题
- 1.问题描述
- 2.思路
- 2.代码
说明
闵老师的文章链接: 日撸 Java 三百行(总述)_minfanphd的博客-CSDN博客
自己也把手敲的代码放在了github上维护:https://github.com/fulisha-ok/sampledata
day35 图的 m 着色问题
1.问题描述
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。如果有一种着色法使G中每条边的2个顶点着不同颜色,则称这个图是m可着色的。图的m着色问题是对于给定图G和m种颜色,找出所有不同的着色法
2.思路
分析:
设M[i]= x(x= 0,1,2,…m ; i = 0,1,2,…n)代表第i节点的颜色x; m=3,n = 3,按理颜色的组合会有m^n
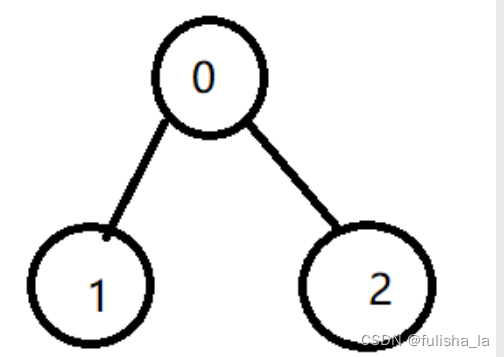
以下图为例,组合会有3^3 = 27种,但是不是所有都可以,有黄色代表冲突
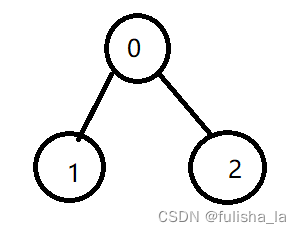
- M[0] = 0,M[1]={0,1,2}, M[2]={0,1,2} 进行颜色排列组合{0,1,1},{0,1,2},{0,2,1},{0,2,2}
- M[0] = 1, M[2]={0,1,2},M[2]={0,1,2}进行颜色排列组合{1,0,0},{1,0,2},{1,2,0},{1,2,2}
- M[0] = 2, M[2]={0,1,2},M[2]={0,1,2}进行颜色排列组合{2,0,0},{2,0,1},{2,1,0},{2,1,1}
在图的着色过程中,我们需要判断是否是邻接点以及颜色是否冲突
其中也有递归的思想在里面,例如我确定了0节点的颜色,我去判断剩下其他节点的颜色。在1,2节点颜色,我确定了1节点颜色,又去判断3节点的颜色。
通过上面的图,画出这个图的空间树去理解还蛮好理解的(其实也思考理解了好久)
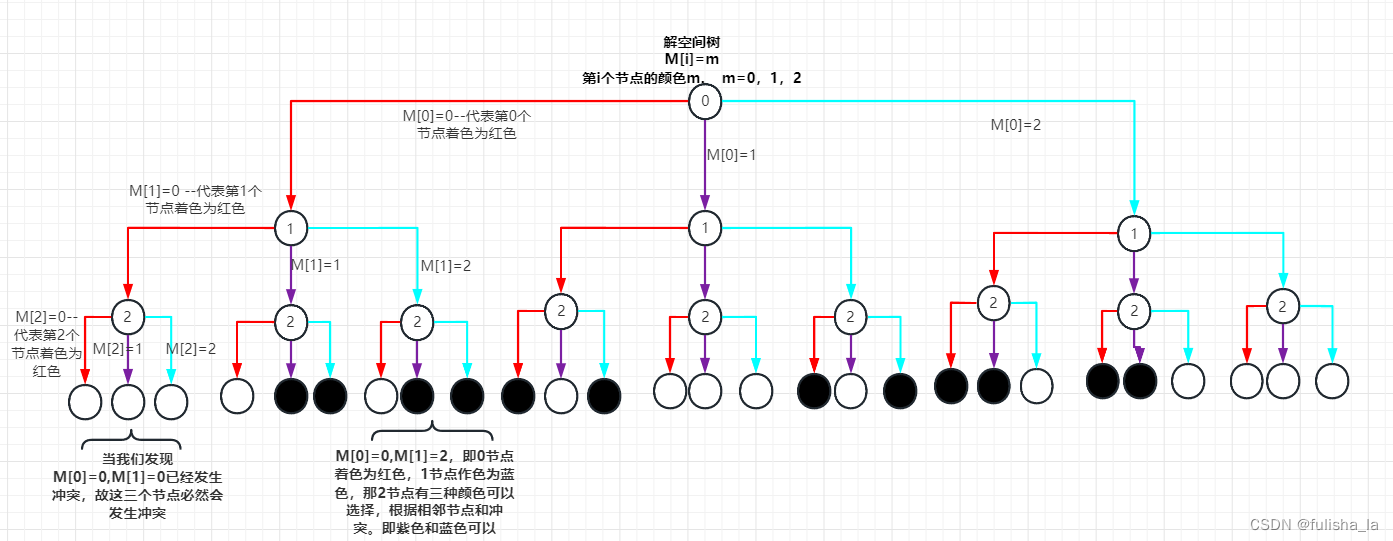
2.代码
- 在前面的分析中有提到递归的思想,所以我们结合上面的解空间树(树我们会常常用到递归),我们为结点0着色后,为其下一个结点着色时如1结点,则需要判断他们是否是相邻节点?是否颜色是不同的?若都满足又往深的递归,若不满足则回溯结点。我觉得图着色问题主要思想也在这里。
public void coloring(int paraNumColors) {
int tempNumNodes = connectivityMatrix.getRows();
int[] tempColorScheme = new int[tempNumNodes];
Arrays.fill(tempColorScheme, -1);
coloring(paraNumColors, 0, tempColorScheme);
}
public void coloring(int paraNumColors, int paraCurrentNumNodes, int[] paraCurrentColoring) {
// Step 1. Initialize.
int tempNumNodes = connectivityMatrix.getRows();
System.out.println("coloring: paraNumColors = " + paraNumColors + ", paraCurrentNumNodes = "
+ paraCurrentNumNodes + ", paraCurrentColoring" + Arrays.toString(paraCurrentColoring));
// A complete scheme.
if (paraCurrentNumNodes >= tempNumNodes) {
System.out.println("Find one:" + Arrays.toString(paraCurrentColoring));
return;
}
// Try all possible colors.
for (int i = 0; i < paraNumColors; i++) {
paraCurrentColoring[paraCurrentNumNodes] = i;
if (!colorConflict(paraCurrentNumNodes + 1, paraCurrentColoring)) {
coloring(paraNumColors, paraCurrentNumNodes + 1, paraCurrentColoring);
}
}
}
public boolean colorConflict(int paraCurrentNumNodes, int[] paraColoring) {
for (int i = 0; i < paraCurrentNumNodes - 1; i++) {
// No direct connection.
if (connectivityMatrix.getValue(paraCurrentNumNodes - 1, i) == 0) {
continue;
}
if (paraColoring[paraCurrentNumNodes - 1] == paraColoring[i]) {
return true;
}
}
return false;
}
public static void coloringTest() {
//int[][] tempMatrix = { { 0, 1, 1, 0 }, { 1, 0, 0, 1 }, { 1, 0, 0, 0 }, { 0, 1, 0, 0 } };
int[][] tempMatrix = { { 0, 1, 1}, { 1, 0, 0 }, { 1, 0, 0 }};
Graph tempGraph = new Graph(tempMatrix);
//tempGraph.coloring(2);
tempGraph.coloring(3);
}
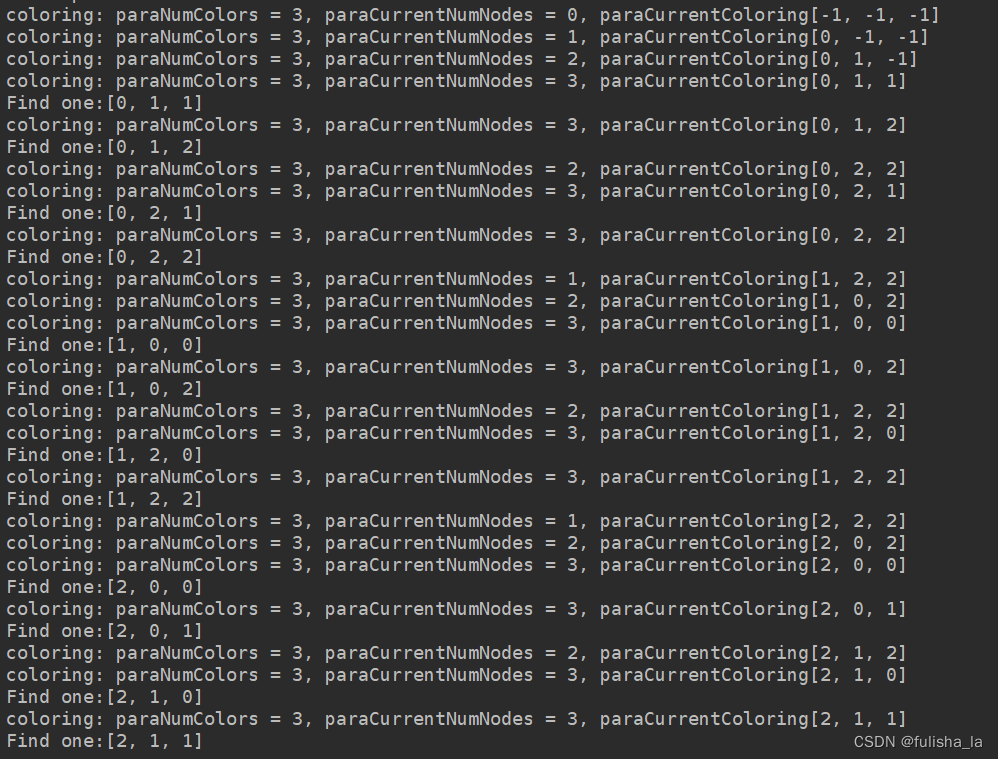
- 测试的例子为上面分析中的例子。