介绍

在这篇文章中，我们看看什么是渠道归因，以及它如何与马尔可夫链的概念联系起来。最近我们被客户要求撰写关于马尔可夫链的研究报告，包括一些图形和统计输出。我们还将通过一个电子商务公司的案例研究来理解这个概念如何在理论上和实践上运作（使用R）。

相关视频：马尔可夫链蒙特卡罗方法MCMC原理与R语言实现|数据分享

马尔可夫链蒙特卡罗方法MCMC原理与R语言实现

，时长08:47

什么是渠道归因？

Google Analytics为归因建模提供了一套标准规则。根据Google的说法，“归因模型是决定销售和转化如何分配给转化路径中的接触点的规则或一组规则。例如，Google Analytics中的最后一次互动模型会为紧接销售或转化之前的最终接触点（即，点击次数）分配100％的功劳。相比之下，第一个互动模型为启动转化路径的接触点分配100％的功劳。“

我们将在本文后面看到最后一个交互模型和第一个交互模型。在此之前，让我们举一个小例子，进一步了解渠道归因。假设我们有一个转换图，如下所示：

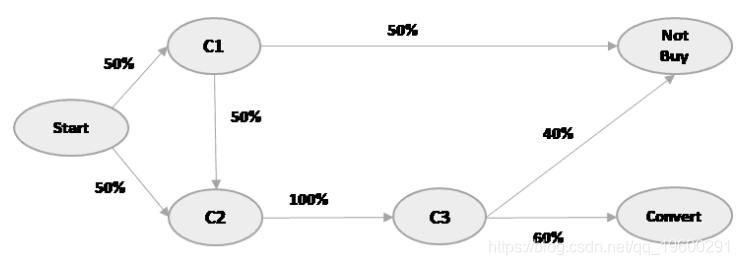
在上述情况下，客户可以通过渠道'C1'或渠道'C2'开始他们的旅程。以C1或C2开始的概率为50％（或0.5）。我们首先计算转换的总体概率，然后进一步查看每个渠道的影响。

P（转换）= P（C1→C2→C3→转换）+ P（C2→C3→转换）

= 0.5 * 0.5 * 1 * 0.6 + 0.5 * 1 * 0.6

= 0.15 + 0.3

= 0.45

马尔可夫链

马尔可夫链是一个过程，它映射活动并给出概率分布，从一个状态转移到另一个状态。马尔可夫链由三个属性定义：

状态空间 - 处理可能存在的所有状态的集合

转换操作 - 从一个状态转移到另一个状态的概率

当前状态概率分布 - 在过程开始时处于任何一个状态的概率分布

我们知道我们可以通过的阶段，从每条路径移动的概率以及我们知道当前状态的可能性。这看起来与马尔可夫链相似。

事实上，这是一个马尔可夫链的应用。如果我们要弄清楚渠道1在我们的客户从始至终转换的过程中的贡献，我们将使用去除效果的原则。去除效果原则说，如果我们想要在客户过程中找到每个渠道的贡献，我们可以通过删除每个渠道并查看在没有该渠道的情况下发生了多少次转化。

例如，我们假设我们必须计算通道C1的贡献。我们将从模型中删除通道C1，并查看图片中没有C1的情况下发生了多少次转换，即所有渠道完好无损时的总转换次数。我们计算渠道C1：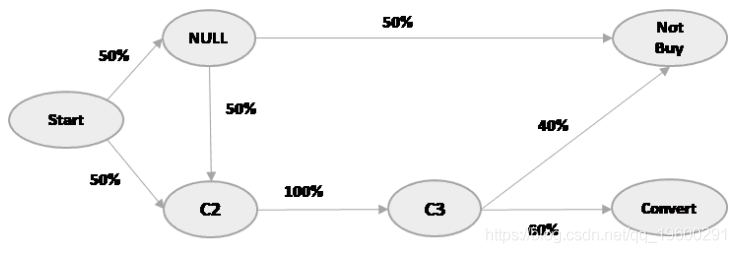

P（去除C1后的转换）= P（C2→C3→转换）

= 0.5 * 1 * 0.6

= 0.3

30％的客户互动可以在没有C1渠道的情况下进行转换; 而C1完好无损，45％的互动可以转换。所以，C1的去除效果是

0.3 / 0.45 = 0.666。

C2和C3的去除效果为1（您可以尝试计算，但直觉地认为，如果我们要删除或者C2或C3，我们将能够完成任何转换？）。

这是马尔可夫链的一个非常有用的应用。在上述情况下，所有渠道--C1，C2，C3（在不同阶段）被称为转换状态 ; 而从一个渠道移动到另一个渠道的概率称为转移概率。

客户旅程是一系列渠道，可以看作是一个有向马尔可夫图中的一个链，其中每个顶点都是一个状态（渠道/接触点），每条边表示从一个状态移动到另一个状态的转移概率。由于到达状态的概率仅取决于之前的状态，因此可以将其视为无记忆马尔可夫链。

电子商务公司案例研究

让我们进行真实案例研究，看看我们如何实施渠道归因建模。

一家电子商务公司进行了一项调查并收集了客户的数据。这可以被认为是具有代表性的人群。在调查中，公司收集了有关客户访问各种触点的数据，最终在其网站上购买该产品。

总共有19个渠道，客户可以遇到产品或产品广告。在19个渠道之后，还有三种情况：

＃20 - 客户决定购买哪种设备;

＃21 - 客户已经做出最终购买；

＃22 - 客户尚未决定。

渠道的总体分类如下：

类别	渠道
网站（1,2,3）	公司的网站或竞争对手的网站
研究报告（4,5,6,7,8）	行业咨询研究报告
在线/评论（9,10）	自然搜索，论坛
价格比较（11）	聚合渠道
朋友（12,13）	社交网络
专家（14）	在线或离线专家
零售店（15,16,17）	实体店
其他（18,19）	其他，例如在各地的促销活动

现在，我们需要帮助电子商务公司确定投资营销渠道的正确策略。应该关注哪些渠道？公司应该投资哪些渠道？我们将在下一节中使用R来解决这个问题。

使用R的实现

我们读取数据，尝试在R中实现并检查结果。

> head(channel)

输出：

R05A.01	R05A.02	R05A.03	R05A.04	…..	R05A.18	R05A.19	R05A.20
16	4	3	5		NA	NA	NA
2	1	9	10		NA	NA	NA
9	13	20	16		NA	NA	NA
8	15	20	21		NA	NA	NA
16	9	13	20		NA	NA	NA
1	11	8	4		NA	NA	NA

我们将进行一些数据处理，将其带入一个阶段，我们可以将其用作模型中的输入。然后，我们将确定哪些客户已进行最终转换。

创建一个特定格式的变量'路径'，可以作为模型的输入。另外，我们将使用“dplyr”包找出每条路径的总发生次数。

路径转变

路径	转换
1 > 1 > 1 > 20	1
1 > 1 > 12 > 12	1
1 > 1 > 14 > 13 > 12 > 20	1
1 > 1 > 3 > 13 > 3 > 20	1
1 > 1 > 3 > 17 > 17	1
> 1 > 6 > 1 > 12 > 20 > 12	1

> channel_fin = ddply(channel_fin,~path,summarise, conversion= sum(convert))
> head(channel_fin)

输出：

路径转变

路径	转换
1 > 1 > 1 > 20	1
1 > 1 > 12 > 12	1
1 > 1 > 14 > 13 > 12 > 20	1
1 > 1 > 3 > 13 > 3 > 20	1
1 > 1 > 3 > 17 > 17	1
1 > 1 > 6 > 1 > 12 > 20 > 12	1

现在，我们将创建一个启发式模型和一个马尔科夫模型，将两者结合起来，然后检查最终结果。

输出：

Output:

渠道名称	首次接触转换	…..	线性接触转换	线性接触值
1	130		73.773661	73.773661
20	0		473.998171	473.998171
12	75		76.127863	76.127863
14	34		56.335744	56.335744
13	320		204.039552	204.039552
3	168		117.609677	117.609677
17	31		76.583847	76.583847
6	50		54.707124	54.707124
8	56		53.677862	53.677862
10	547		211.822393	211.822393
11	66		107.109048	107.109048
16	111		156.049086	156.049086
2	199		94.111668	94.111668
4	231		250.784033	250.784033
7	26		33.435991	33.435991
5	62		74.900402	74.900402
9	250		194.07169	194.07169
15	22		65.159225	65.159225
18	4		5.026587	5.026587
19	10		12.676375	12.676375

输出：

渠道名称	总体转换	总体转换值
1	82.482961	82.482961
20	432.40615	432.40615
12	83.942587	83.942587
14	63.08676	63.08676
13	195.751556	195.751556
3	122.973752	122.973752
17	83.866724	83.866724
6	63.280828	63.280828
8	61.016115	61.016115
10	209.035208	209.035208
11	118.563707	118.563707
16	158.692238	158.692238
2	98.067199	98.067199
4	223.709091	223.709091
7	41.919248	41.919248
5	81.865473	81.865473
9	179.483376	179.483376
15	70.360777	70.360777
18	5.950827	5.950827
19	15.545424	15.545424

在进一步讨论之前，我们先来了解一下我们上面看到的一些术语的含义。

第一次接触转换：当该渠道是客户的第一个触点时，通过渠道进行的转换。第一个触点获得100％的功劳。

上次接触转换：当该渠道是客户的最后一个接触点时，通过渠道发生的转化。100％功劳给予最后的接触点。

回到R代码，让我们合并这两个模型，并以可视化方式表示输出。

# 绘制总转换
ggplot(R1, aes(channel_name, value, fill = variable)) +
  geom_bar(stat='identity', position='dodge') +

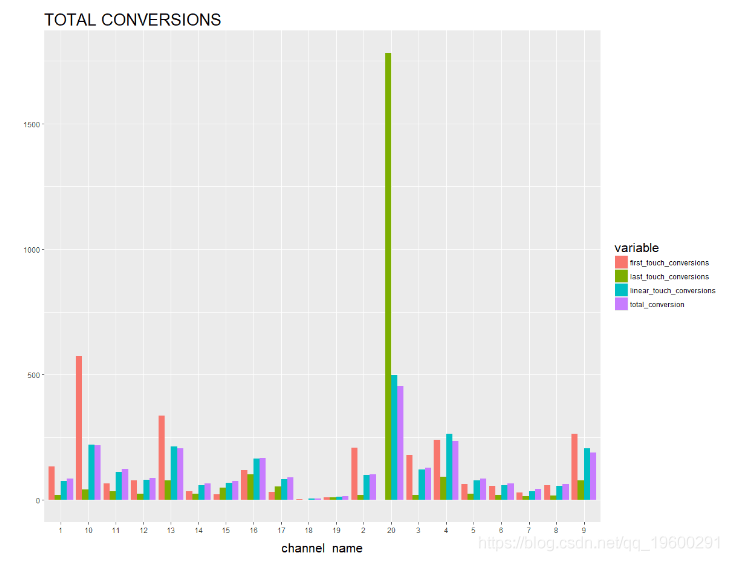
从上图中可以清楚地看到结果。从第一次接触转换角度来看，渠道10，渠道13，渠道2，渠道4和渠道9非常重要; 而从最后接触的角度来看，第20渠道是最重要的（因为在我们的例子中客户决定购买哪种产品）。就线性接触转换而言，渠道20、渠道4和渠道9是重要的。从总转换角度来看，渠道10,13,20,4和9非常重要。