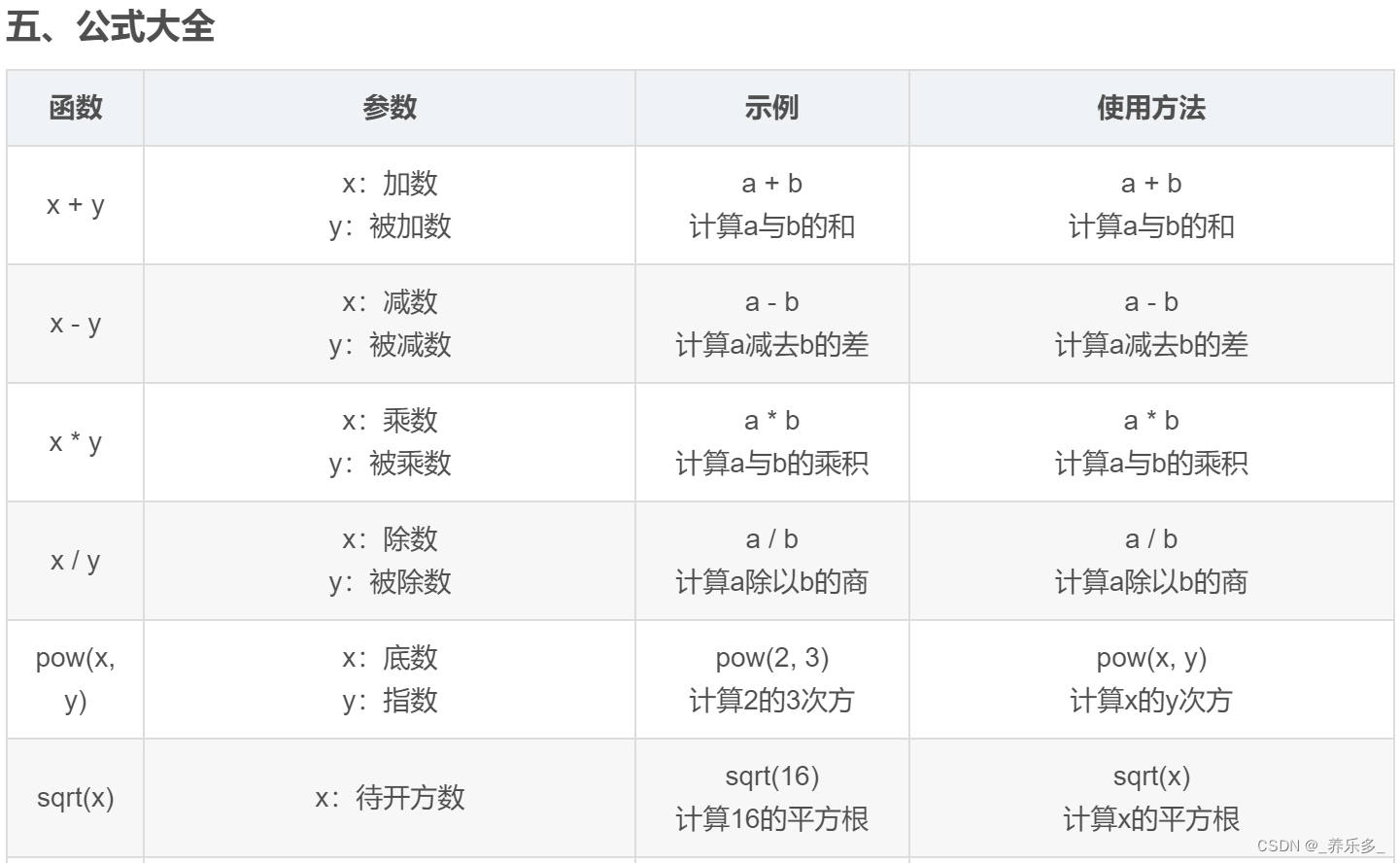
写作业时重新理了下，如果有问题欢迎指正！

1. 说是回归，其实就是个分类，用【0，1】标记结果y是录取还是录取，而影响结果y的就是X(x₀,x₁,…x_n-1)。
2. 怎么判断结果y是0还是1用到的是逻辑回归函数（也叫假设函数，随便怎么叫）
   $h_{\theta }(x)=\frac{1}{1+e^{-\theta .Tx}}$（.T是矩阵的转置，θ和x都是矩阵的形式。实际代码实现中用矩阵进行计算更方便），当$z=-\theta .Tx$为0（正好卡在决策函数上，决策函数就是分类的那条线，后面还会说），预测结果发生概率为0.5，在决策函数的A部分就往1趋近，反之往0趋近。
   逻辑回归函数的作用，网上搜的规范点说法：将取值范围(−∞,+∞)映射到(0,1) 之间，更适宜表示预测的概率，即事件发生的“可能性” 。
   
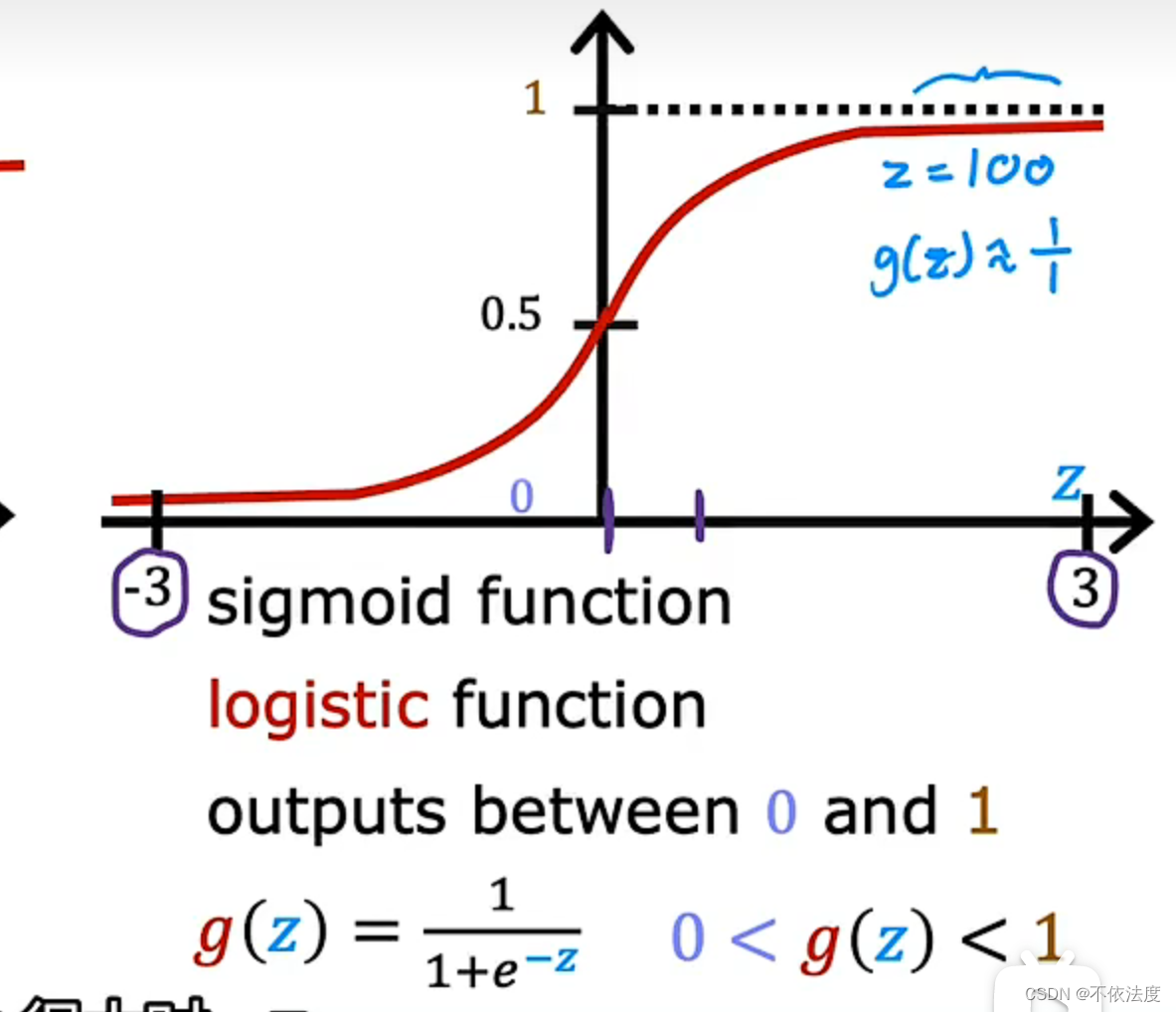
   3.$z=-\theta .Tx$，$\theta .Tx$ 这个就是决策函数，也就是y = θ₀x₀ + θ₁x₁（假设就两个参数，而且次数都是1），矩阵theta 包括 θ₀ + θ₁ + θ₂ + … + θ_n-1，矩阵x包括x₀ + x₁ + x₂ + … + x_n-1。
   决策函数的作用就是把0和1的结果隔离开，逻辑回归函数的作用就是计算预测结果的可能性。
3. 为了获取最合适的决策函数，需要代价函数来计算代价最小时的theta（梯度下降）。这里计算代价不能再用线性回归的代价函数了，会有多个局部最值。（详细可以看吴恩达教授的视频，b站就有）
   这是逻辑回归的代价函数，推导可以看这个https://blog.csdn.net/W_Y_J_love/article/details/105415927。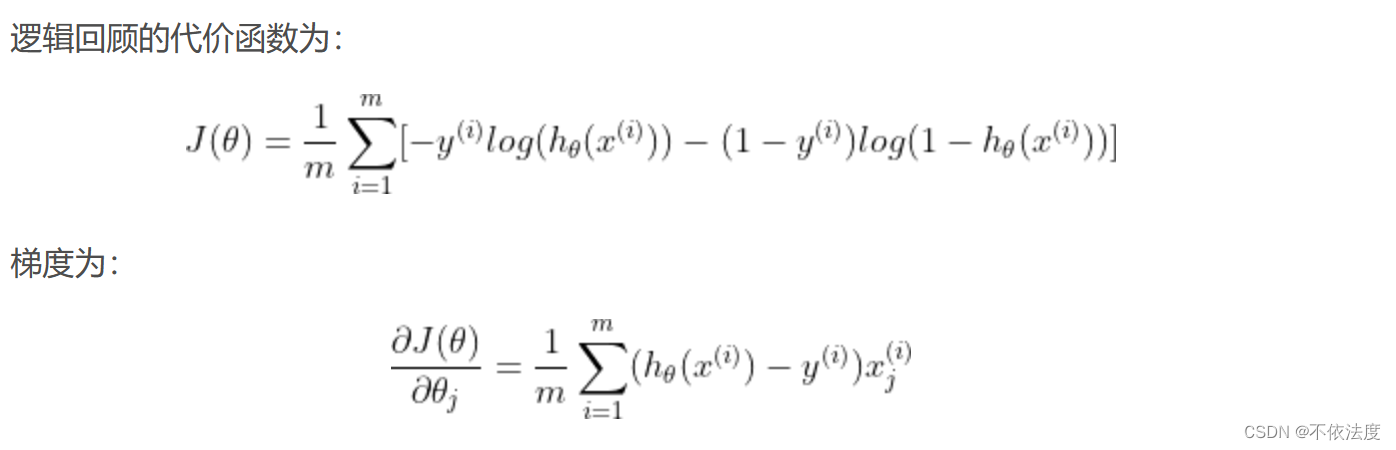
4. 总的来说就是根据代价函数求出满足训练数据集的代价最小的theta。
5. 但是！如果数据不够还追求代价函数最小化，很有可能导致过拟合，再导入新的数据就可能出现大麻烦！所以请考虑一下正则化，目的就是为了不让决策函数过拟合。不理解正则化原理可以看看这个https://zhuanlan.zhihu.com/p/345566088。

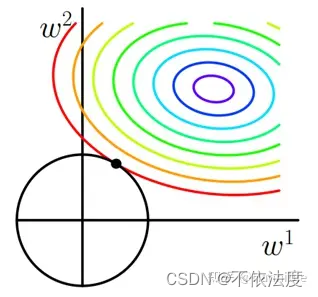
   • 正则化是从θ₁开始而不是从θ₀。
     

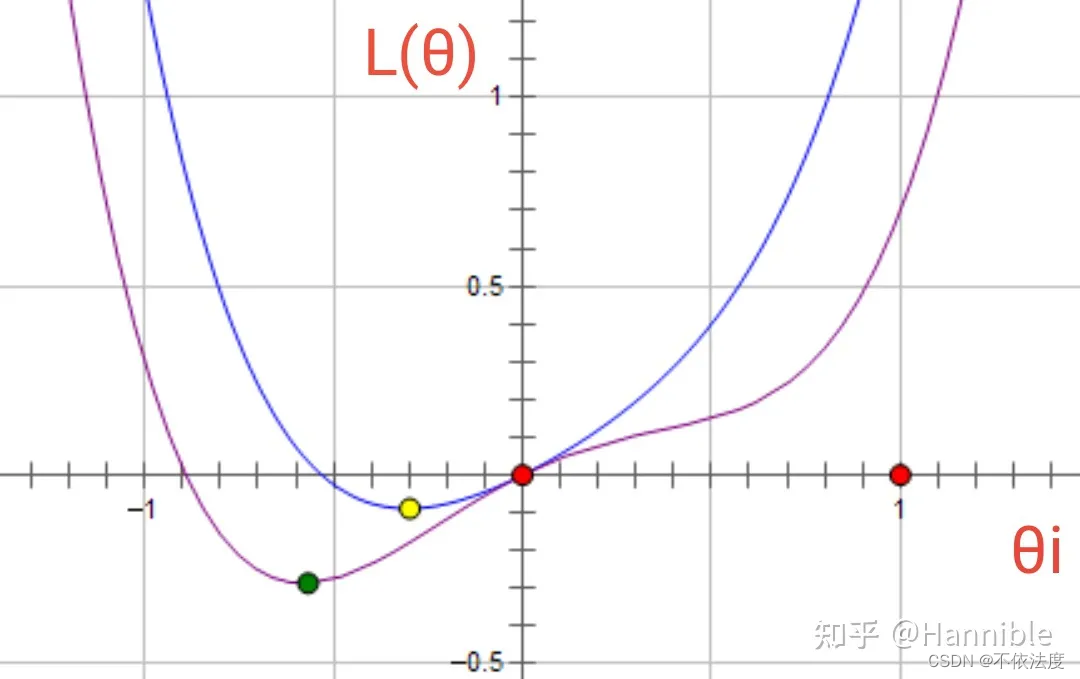
   • 正则化函数引入参数λ，共同影响了在计算回归函数的代价函数的最小值的取值（λ与θ相互制约，谁也不让谁太过分）（听起来有点绕hh），其实就是极值点因为引入的正则化函数偏移了。
     

   • 正则化函数取θ²更温和， 不会直接把大量的特征归零。（看图）