---

一、Simple Graphics

1. 用 plot（）函数画图

x 和 y：这是绘制散点图时用到的 x 和 y 坐标的数值。通常，x 和 y 是等长的数值向量。

① type：指定绘图的类型。可选值有：

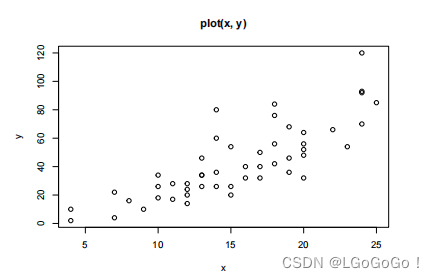
“p”（点图，缺省值）

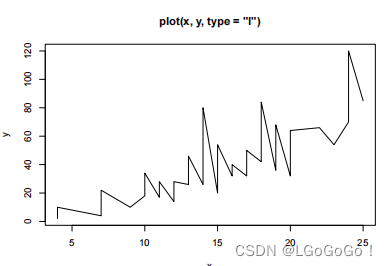
“l”（折线图）

“b”（点和线都画）

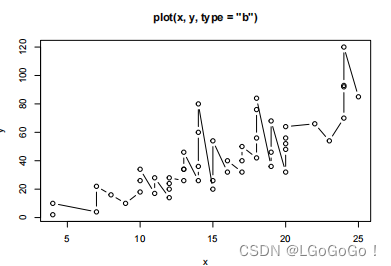
“c”（仅连接线）
“o”（点和线都画，线在点上）
“h”（直方图样式）
“s”（阶梯图）
“n”（不绘制任何图形，仅绘制坐标轴）

② main：用于指定图形的标题。

③ xlab 和 ylab：分别用于指定 x 轴和 y 轴的标签。

④ xlim 和 ylim：分别用于指定 x 轴和 y 轴的数值范围，例如：xlim = c(0, 10)。

⑤ col：指定点或线的颜色。

⑥ pch：指定点的形状，可选值为整数或字符。常见的整数形状包括：0（方形），1（圆形），2（三角形），等等。也可以使用字符（如 “a”、“b”、“c”）作为点的形状。

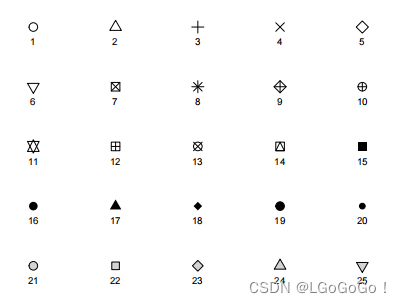
⑦ lty：指定线的类型，可选值为整数或字符。例如：1（实线，缺省值），2（虚线），3（点线），等等。

The line type can be specified by name: “solid”, “dashed”, “dotted”, “dotdash”, “longdash”, “twodash”

⑧ lwd：指定线的宽度，数值越大，线越粗。

例如：

> x <- 1:10
> y <- x^2
> plot(x, y, type = "b", col = "red", lwd = 2, pch = 16, main = "A Simple Plot", xlab = "X-axis", ylab = "Y-axis")

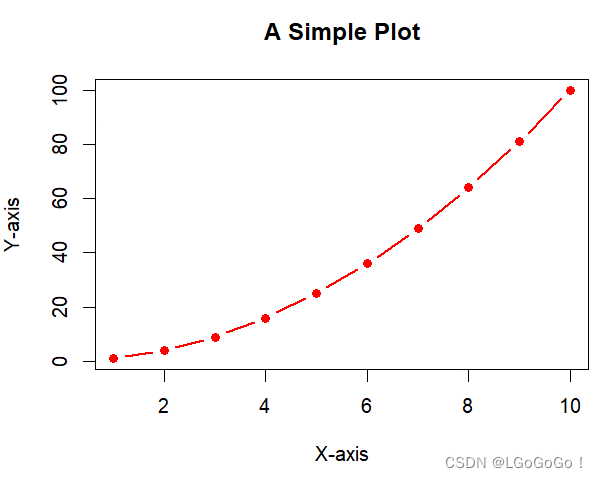
二、Optimization

Optimization is the process of finding a minimum or maximum for a function.

1. 简单求最值

使用 optimize（） 函数：

# 找 sin 函数的最值
> optimize(sin, lower = 0, upper = 3,
maximum = TRUE, tol = 1e-10)
$maximum
[1] 1.5708
$objective
[1] 1
> pi/2
[1] 1.5708

2. Interpolation（插值）

插值是在已知一组给定点（xi, yi），i = 0, 1, …, n 的情况下，寻找一个函数 f(x)，使其恰好穿过这些点。在这里，我们假设 x0 < x1 < x2 < … < xn，提供了一种在仅知道少数值时，可视化整个函数外观的方法。

样条插值（Spline Interpolation）使用多项式（通常为低阶）在给定值之间进行插值。相邻的多项式在它们的公共端点处达成一致（因为它们进行插值），并且可以使连接平滑（即导数连续）。

三次样条（Cubic Splines）是实践中最常用的样条。三次样条需要具有以下属性：

---

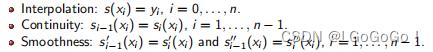
插值例：
通过样条插值法来估计一组观测数据（月平均气温）之间的平滑函数：

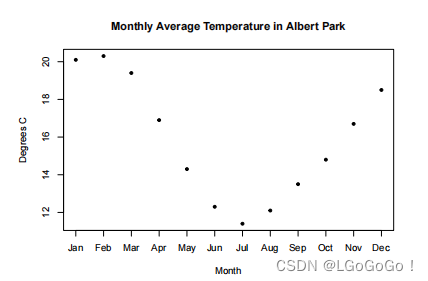
> xm = 1:13 + .5
> ym = c(20.1, 20.3, 19.4, 16.9, 14.3, 12.3, 11.4,
12.1, 13.5, 14.8, 16.7, 18.5, 20.1)
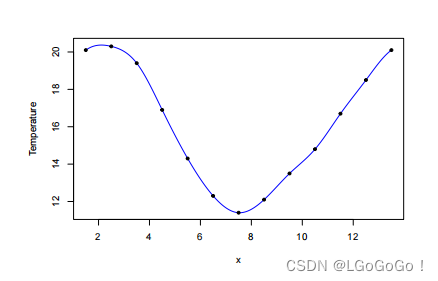
# 由于气温在12月到1月间具有周期性变化，所以选择使用周期样条
> f = splinefun(xm, ym, method = "periodic")

> x = seq(1.5, 13.5, length = 2000)
> plot(x, f(x), type = "l", col = "blue",
ylab = "Temperature")
> points(xm, ym, pch=20)

3. optim（）函数

optimize 函数只适用于单变量函数的优化问题。当需要优化的函数包含两个或更多变量时，必须使用名为 optim 的函数。

optim 函数适用于平滑函数和非平滑函数。但如果函数是平滑的，通过指定针对平滑函数的方法，可以获得更好的性能。optim 函数提供了几种可通过 method 参数指定的方法。

默认的 “Nelder-Mead” 方法既适用于平滑函数，也适用于非平滑函数。然而，对于平滑函数，建议使用 “BFGS” 方法，因为它在优化平滑函数时的性能更佳。

使用 optim 函数例：
我们有如下表达式用于拟合一组数据：

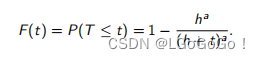
但需确定 a 与 h 的值，才能得到最终的表达式，在这个例子中，我们试图找到一组参数 a 和 h（theta[1] 和 theta[2]），使得卡方统计量尽可能小。我们定义了一个函数 Q，用于计算给定参数 a 和 h 时的卡方统计量。

我们使用 R 中的 optim 函数来最小化 Q 函数，从初始值 θ = (5, 10) 开始优化过程：

> Q = function(theta)
	chi2(Hutterites,
		342 * diff(F(breaks, theta[1], theta[2])))

z = optim(c(5, 10), Q, method = "BFGS")

> z$par
[1] 3.1263 9.5822
> z$value
[1] 16.764

在参数 a 和 h 分别取 3.1263 和 9.5822 时，我们得到了卡方统计量的最小值 16.764。

再以此结果计算 p-value：

> pchisq(z$value, 13, lower=FALSE)
[1] 0.2103

得到的p值为0.2103。通常情况下，如果p值大于显著性水平（如0.05），则认为没有足够证据拒绝原假设。在这个例子中，原假设是估计的a和h值下的模型可以合理地描述数据。因为p值大于0.05，所以我们没有足够证据拒绝原假设，这意味着使用估计的a和h值的模型确实可以合理地描述数据。

[注]
① 为什么使得卡方统计量尽可能小？
卡方统计量（chi-square statistic）是衡量观察值与理论值之间差异的一种方法。在统计建模和拟合中，我们通常希望模型能够尽可能地拟合观察到的数据。为了实现这个目标，我们需要找到一组参数，使得模型的预测值与观测值之间的差异最小。

卡方统计量是一种衡量这种差异的方法，它计算了观察值与期望值（模型预测值）之间的偏差的平方和，然后将这些平方和归一化。通过最小化卡方统计量，我们可以找到一组参数，使得模型的预测值与实际观测值之间的差异最小。这样，我们就可以得到一个拟合效果较好的模型。

需要注意的是，卡方统计量并不总是适用于所有类型的拟合问题。它主要适用于计数或分类数据，或者数据服从某种已知分布的情况。在其他情况下，可能需要使用其他度量方法来衡量模型的拟合效果，例如均方误差（MSE）、最大似然估计（MLE）等。

② z $ convergence 的值为多少说明收敛？
在R中，optim函数的输出包含一个名为convergence的组件。z $ convergence的值为0表示优化过程正常收敛。如果 z $ convergence的值非0，那么说明优化过程可能没有正常收敛，可能需要调整初始参数值、优化方法或其他相关设置。在这种情况下，输出的结果可能不是一个可靠的最优解。

总之，如果 z$convergence 的值为0，那么说明优化过程已经正常收敛，可以信任并分析输出的结果。