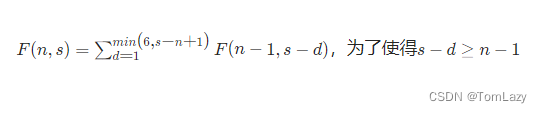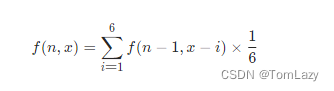题目链接:https://leetcode.cn/problems/nge-tou-zi-de-dian-shu-lcof/
1. 题目介绍(60. n个骰子的点数)
把n个骰子扔在地上,所有骰子朝上一面的点数之和为
s。输入n,打印出s的所有可能的值出现的概率。
你需要用一个浮点数数组返回答案,其中第
i个元素代表这n个骰子所能掷出的点数集合中第i小的那个的概率。
【测试用例】:
- 掷骰子模拟器:还蛮有意思的。
示例 1:
输入: 1
输出: [0.16667,0.16667,0.16667,0.16667,0.16667,0.16667]
示例 2:
输入: 2
输出: [0.02778,0.05556,0.08333,0.11111,0.13889,0.16667,0.13889,0.11111,0.08333,0.05556,0.02778]
【条件约束】:
限制:
- 1 <= n <= 11
【相关题目】:
题目1:计算n次掷有k个面的骰子实现给定和的方法总数 – Techie Delight
……
例如:
……
Input:
- The total number of throws n is 2
- TThe total number of faces k is 6 (i.e., each dice has values from 1 to 6)
- TThe desired sum is 10
……
Output:
- The total number of ways is 3.
- The possible throws are (6, 4), (4, 6), (5, 5)
2. 前置知识
在掷骰子中探索组合的奥秘 – Komorebi
2.1 K - 骰子组合
给定骰子数,得到所有可能的组合
……
示例1:
输入:K = 2
输出:[(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6), (2, 1 ), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6), (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4 , 6), (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (6, 1), (6, 2 ), (6, 3), (6, 4), (6, 5), (6, 6)]
解释:打印所有可能的组合。
……
示例2:
输入:K = 1
输出:[(1, ), (2, ), (3, ), (4, ), (5, ), (6, )]
解释:打印所有可能的组合。
因为该题要求我们求出所有骰子🎲点数和的概率,那么我们首先要知道的就是 K个骰子一共有多少种组合的可能(允许重复),因为正常的骰子是 六面体,具有六个面,因此我们就可以得到公式 6k 来求出骰子组合的所有可能。
下面我们可以通过程序来验证一下公式是否正确:(以6个骰子为例)
2.1.1 Python版本
代码参考:Python – K Dice Combinations
# Python3 code to demonstrate working of
# K Dice Combinations
# Using list comprehension + product()
from itertools import product
# initializing K
K = input("请输入骰子个数:")
# using list comprehension to formulate elements
temp = [list(range(1, 7)) for _ in range(int(K))]
# using product() to get Combinations
res = list(product(*temp))
# printing result
print("The constructed dice Combinations : " + str(res))
我们可以看到,当有 6 个骰子时,其组合的所有可能为 46656,与我们通过公式使用计算器得来的结果一致:


2.1.2 Java版本
该方法基于 回溯 模板实现,通过不断向当前组合中添加数字,并在到达目标长度时将其添加到结果集中,最后返回所有可能的组合。
// 返回 K 个骰子的所有可能的组合
public static List<List<Integer>> getCombinations(int n) {
List<List<Integer>> res = new ArrayList<>();
List<Integer> cur = new ArrayList<>();
backtrack(n, cur, res);
// 回溯结束,返回所有可能的组合
return res;
}
private static void backtrack(int n, List<Integer> cur, List<List<Integer>> res) {
// 到达目标长度时将其添加到结果集中
if (cur.size() == n) {
res.add(new ArrayList<>(cur));
return;
}
// 遍历所有可能
for (int i = 1; i <= 6; i++) {
cur.add(i);
backtrack(n, cur, res);
// 移除 cur 列表中的最后一个元素
cur.remove(cur.size() - 1);
}
}
运行结果:
3. 题解
3.1 动态规划(二维数组) – O(n2)
时间复杂度 O(n2),空间复杂度 O(n2)
【解题思路】:
骰子一共有 6 个面,每个面上都有一个点数,对应的是 1~6 之间的一个数字。所以 n 个骰子的点数和的最小值为 n,最大值为 6n,即点数和范围为[n,6n]。另外根据排列组合的知识,我们还知道 n 个骰子的所有点数的排列数为 6n 。要解决这个问题,我们需要先统计出每个点数出现的次数,然后把每个点数出现的次数除以 6n,就能求出每个点数出现的概率。
……
依据上面的思想,我们可以使用 动态规划 来进行求解:
……
我们假设f(n,s)为 当骰子数为n,点数和为 s 时情况的出现的总数量,那么 当 n=1 时,就有f(1,s) = 1,其中 s = 1,2,3,4,5,6;当 n ≥ 2 时,f(n,s) = f(n−1,s−1) + f(n−1,s−2) + f(n−1,s−3) + f(n−1,s−4) + f(n−1,s−5) + f(n−1,s−6),转化为公式,即:
……
【实现策略】:
根据前面推理得到的公式,我们就可以进行以下编码:
- 定义二维数组
dp,用来记录f(n,s)的值,而由于下方for循环会取到 n和 6n,为了防止数组越界,所以数组的长度必须+1,同时空出 0 位不用;以 n = 6 为例:(Note:这里 [6n+1] 确实造成造成了不小的空间浪费,因为最后一层的实际范围位 [5*n+1],而其他层则是更小)
- 开始根据公式进行 动态规划,当
n = 1时,怎么怎么样,当n >= 2时,怎么怎么样;- 动规结束后,我们就可以求出 骰子所有点数的排列数
total,让 dp 数组中的最后一层 依次除以 总排列数,并将得到的结果存入ans后返回。
class Solution {
// Solution2:二维数组:动态规划
public double[] dicesProbability(int n) {
// 下方for循环会取到 n 和 6*n, 所以这里的数组长度必须+1
int [][]dp = new int[n+1][6*n+1];
//边界条件:
// 当n = 1时,F(1,s)=1,其中s=1,2,3,4,5,6
for(int s = 1; s <= 6; s++) dp[1][s] = 1;
// 当n ≥ 2时,F(n,s)=F(n−1,s−1) + F(n−1,s−2) + F(n−1,s−3) + F(n−1,s−4) + F(n−1,s−5) + F(n−1,s−6)
for(int i = 2; i<=n; i++){
for(int s = i; s <= 6*i; s++){
//求dp[i][s],即 f(n,s)
for(int d = 1; d <= 6; d++){
if(s-d < i-1) break;//为0了
dp[i][s] += dp[i-1][s-d];
}
}
}
// total表示总的排列数
double total = Math.pow((double)6,(double)n);
// ans表示s的所有取值:[n,6n]
double[] ans = new double[5*n+1];
// 开始计算概率
for(int i = n; i <= 6*n; i++){
ans[i-n]=((double)dp[n][i])/total;
}
// 计算完成,返回结果
return ans;
}
}

3.2 动态规划改进(一维数组) – O(n2)
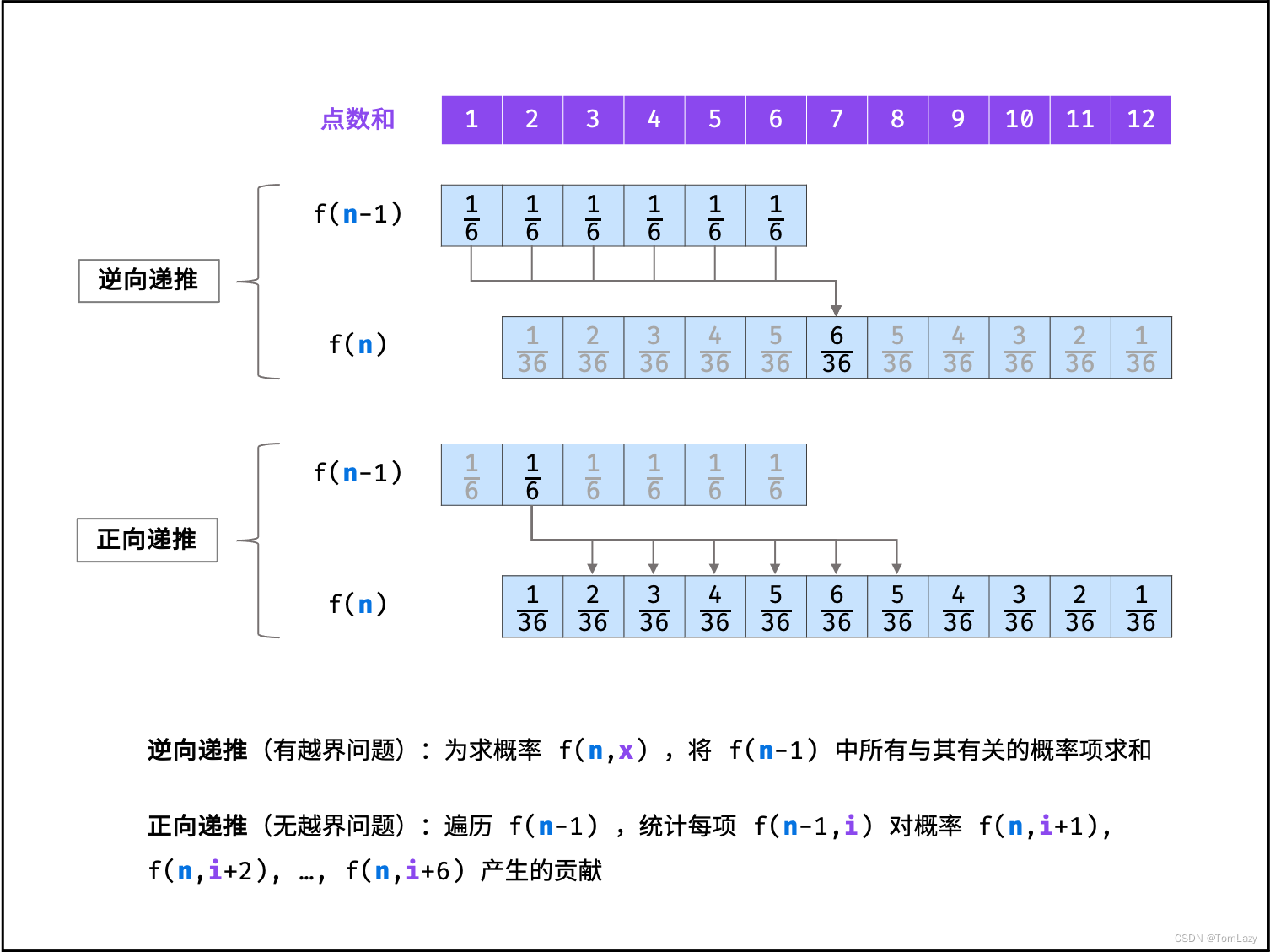
状态转移公式:(与3.1 略有不同)
假设已知 n−1 个骰子的解f(n−1),此时添加一枚骰子,求 n 个骰子的点数和为 x 的概率f(n,x)
……
该题的通常做法是声明一个二维数组 dp,dp[i][j]代表前 i 个骰子的点数和 j 的概率,并执行状态转移。而由于dp[i]仅由dp[i−1]递推得出,为降低空间复杂度,只建立两个一维数组 dp , tmp 交替前进即可。
class Solution {
// Solution2:动态规划
// 递推公式:f(n,s) = f(n-1.s-1)/6 + f(n-1.s-2)/6 + …… + f(n-1.s-6)/6
public double[] dicesProbability(int n) {
//因为最后的结果只与前一个动态转移数组有关,所以这里只需要设置一个一维的动态转移数组
//原本dp[i][j]表示的是前i个骰子的点数之和为j的概率,现在只需要最后的状态的数组,所以就只用一个一维数组dp[j]表示n个骰子下每个结果的概率。
//初始是1个骰子情况下的点数之和情况,就只有6个结果,所以用dp的初始化的size是6个
double[] dp = new double[6];
//只有一个数组
Arrays.fill(dp,1.0/6.0);
//从第2个骰子开始,这里n表示n个骰子,先从第二个的情况算起,然后再逐步求3个、4个···n个的情况
//i表示当总共i个骰子时的结果
for(int i=2;i<=n;i++){
//每次的点数之和范围会有点变化,点数之和的值最大是i*6,最小是i*1,i之前的结果值是不会出现的;
//比如i=3个骰子时,最小就是3了,不可能是2和1,所以点数之和的值的个数是6*i-(i-1),化简:5*i+1
//当有i个骰子时的点数之和的值数组先假定是temp
double[] temp = new double[5*i+1];
//从i-1个骰子的点数之和的值数组入手,计算i个骰子的点数之和数组的值
//先拿i-1个骰子的点数之和数组的第j个值,它所影响的是i个骰子时的temp[j+k]的值
for(int j=0;j<dp.length;j++){
//比如只有1个骰子时,dp[1]是代表当骰子点数之和为2时的概率,它会对当有2个骰子时的点数之和为3、4、5、6、7、8产生影响,因为当有一个骰子的值为2时,另一个骰子的值可以为1~6,产生的点数之和相应的就是3~8;比如dp[2]代表点数之和为3,它会对有2个骰子时的点数之和为4、5、6、7、8、9产生影响;所以k在这里就是对应着第i个骰子出现时可能出现六种情况,这里可能画一个K神那样的动态规划逆推的图就好理解很多
for(int k=0;k<6;k++){
//这里记得是加上dp数组值与1/6的乘积,1/6是第i个骰子投出某个值的概率
temp[j+k]+=dp[j]*(1.0/6.0);
}
}
//i个骰子的点数之和全都算出来后,要将temp数组移交给dp数组,dp数组就会代表i个骰子时的可能出现的点数之和的概率;用于计算i+1个骰子时的点数之和的概率
dp = temp;
}
return dp;
}
}
4. 参考资料
[1] 动态规划 – shy
[2] 剑指 Offer 60. n 个骰子的点数(动态规划,清晰图解)-- Krahets