- 特征缩放的作用
- 特征缩放可以让梯度下降算法运行的更快
- 特征:X 对应的参数:W
- 当一个特征的可能值范围很大时,一个好的模型会选择一个相对较小的对应参数值,因为W₁的一个非常小的变化会给估计价格产生非常大的影响,同时也会对成本函数J产生非常大的影响。
- 同样,当一个特征的可能值范围很小时,一个好的模型会选择一个相对较大的对应参数值,而W₂需要非常大的变化才能给估计价格产生非常大的影响,对成本函数J也是如此。如图:
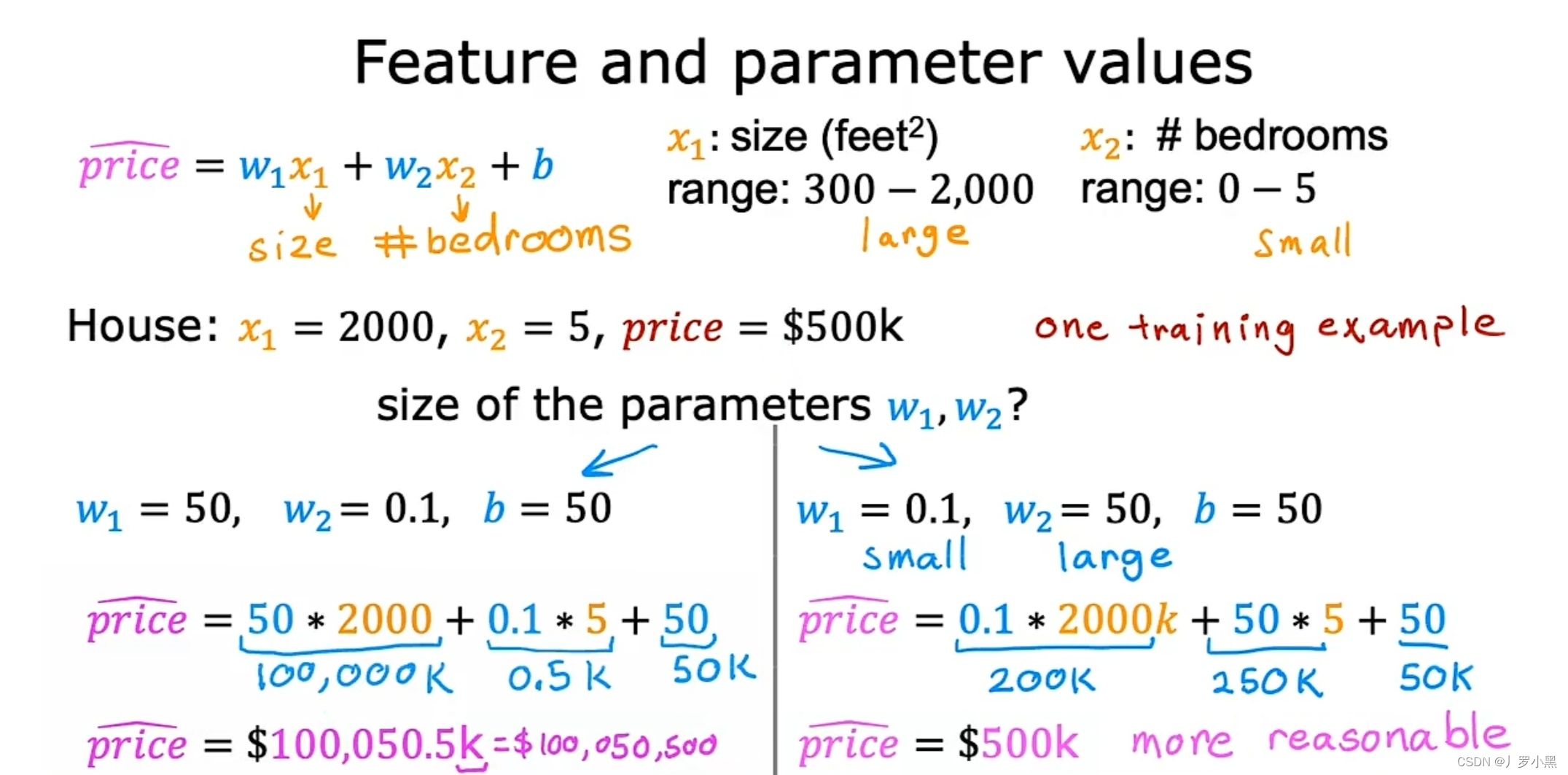
- 当两个特征的可能值范围差距过大时,所对应的参数的可能值范围差距也会过大,产生的成本函数的等高线图为椭圆形,如图:
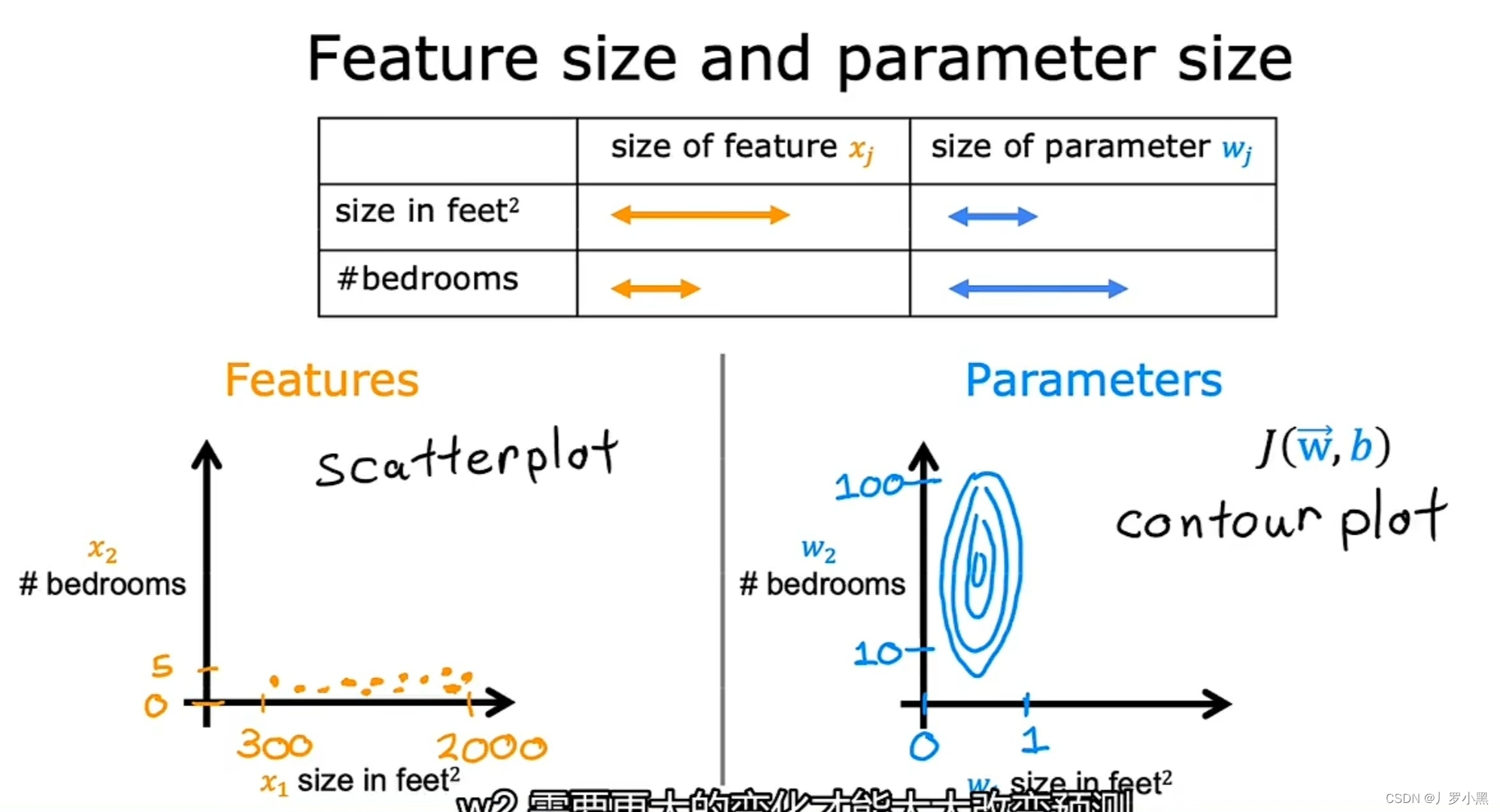
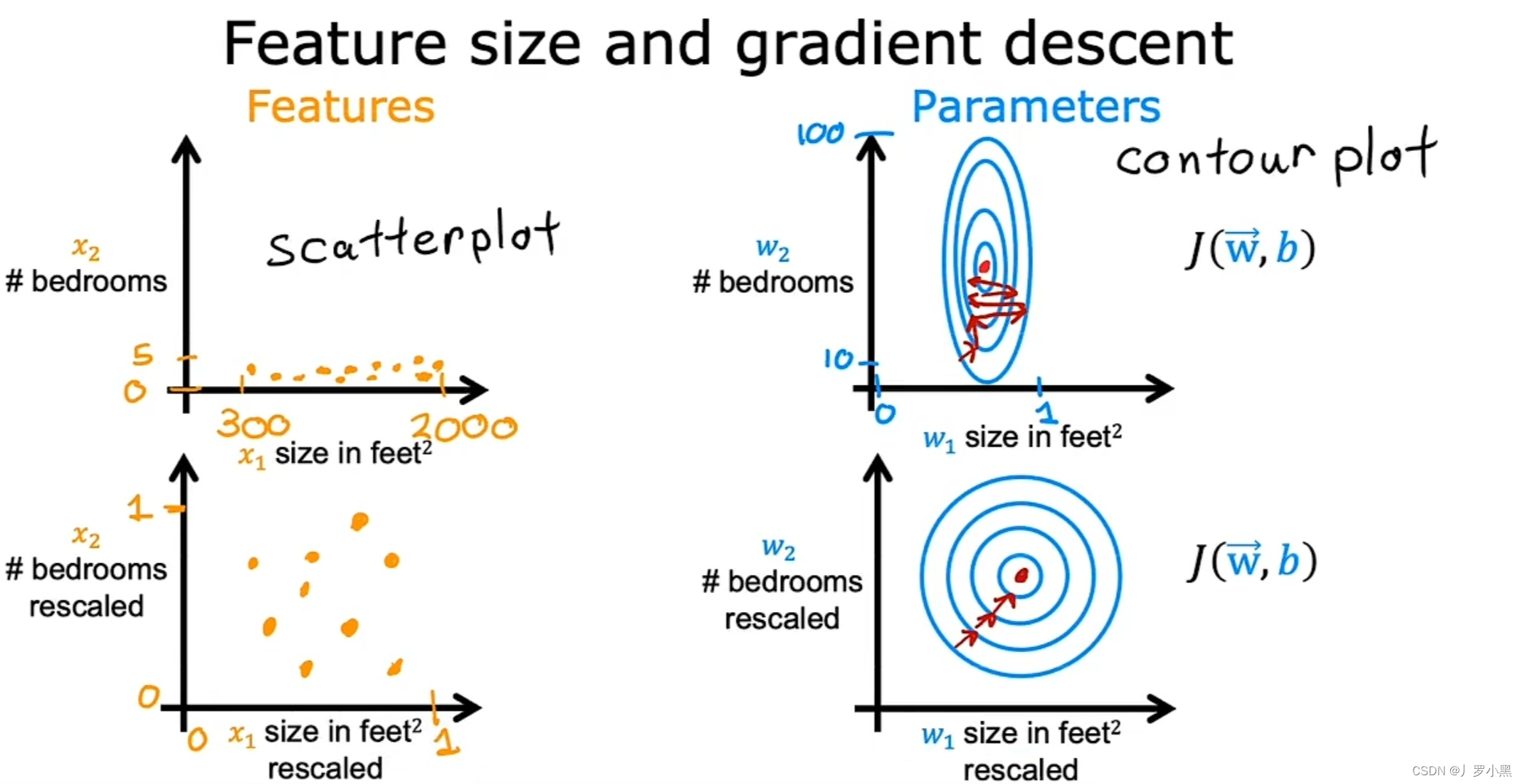
- 若J函数的等高线图为椭圆形,又高又瘦时,会让梯度下降算法在运行时来回横跳很长一段时间,才能找到J函数的全局最小值。
- 此时,我们可以进行特征缩放,即对训练数据进行一些转换,使特征的可能值范围都是彼此可比较的。用转换后的数据重新画成本函数J的等高线图,J函数为圆形,此时采用梯度下降算法,可以找到一条更直接的通往全局最小值的路,不会再左右横跳浪费时间了。如图:
- 常见的特征缩放方法
- 除以最大值法:
- 将特征的可能值均除以可能值范围的最大值
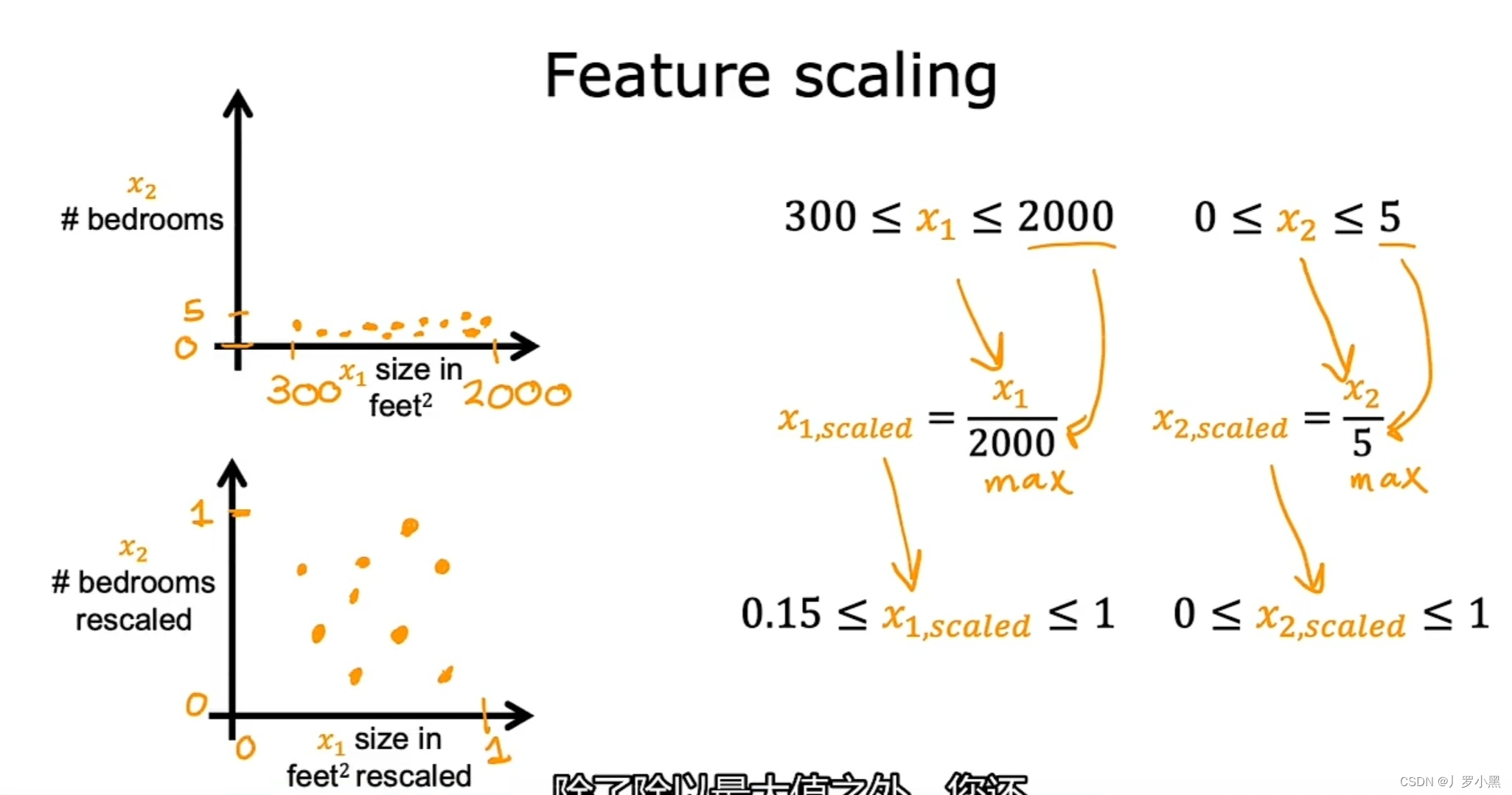
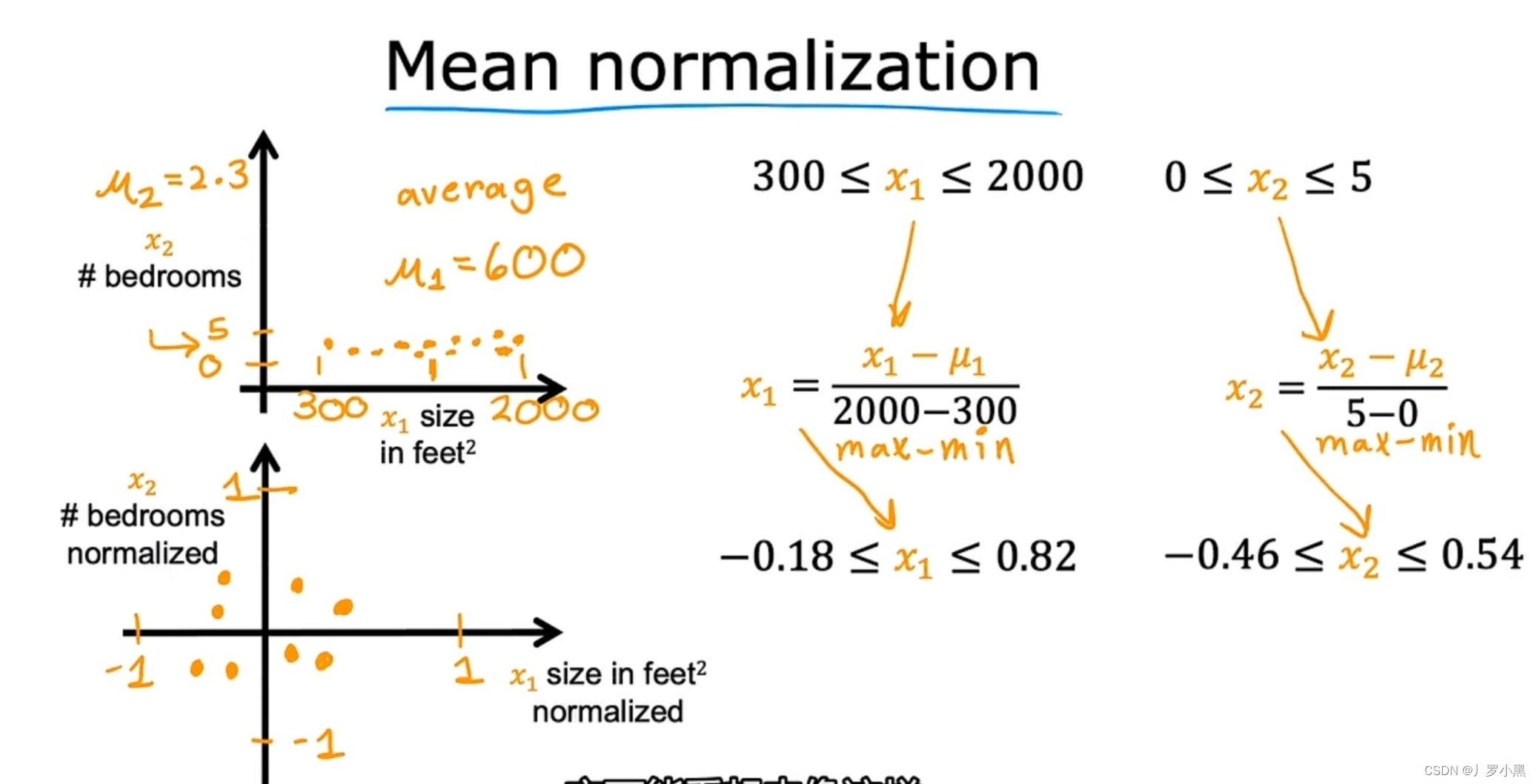
- 均值归一化:
- 特征的可能值以前可能都大于零,进行均值归一化后,可以使特征的可能值会围绕零点,既有负值又有正值
- 步骤:首先求某特征的平均值,再将该特征的可能值先减去该特征的平均值,再除以,可能值范围的最大值与最小值的差。如图:
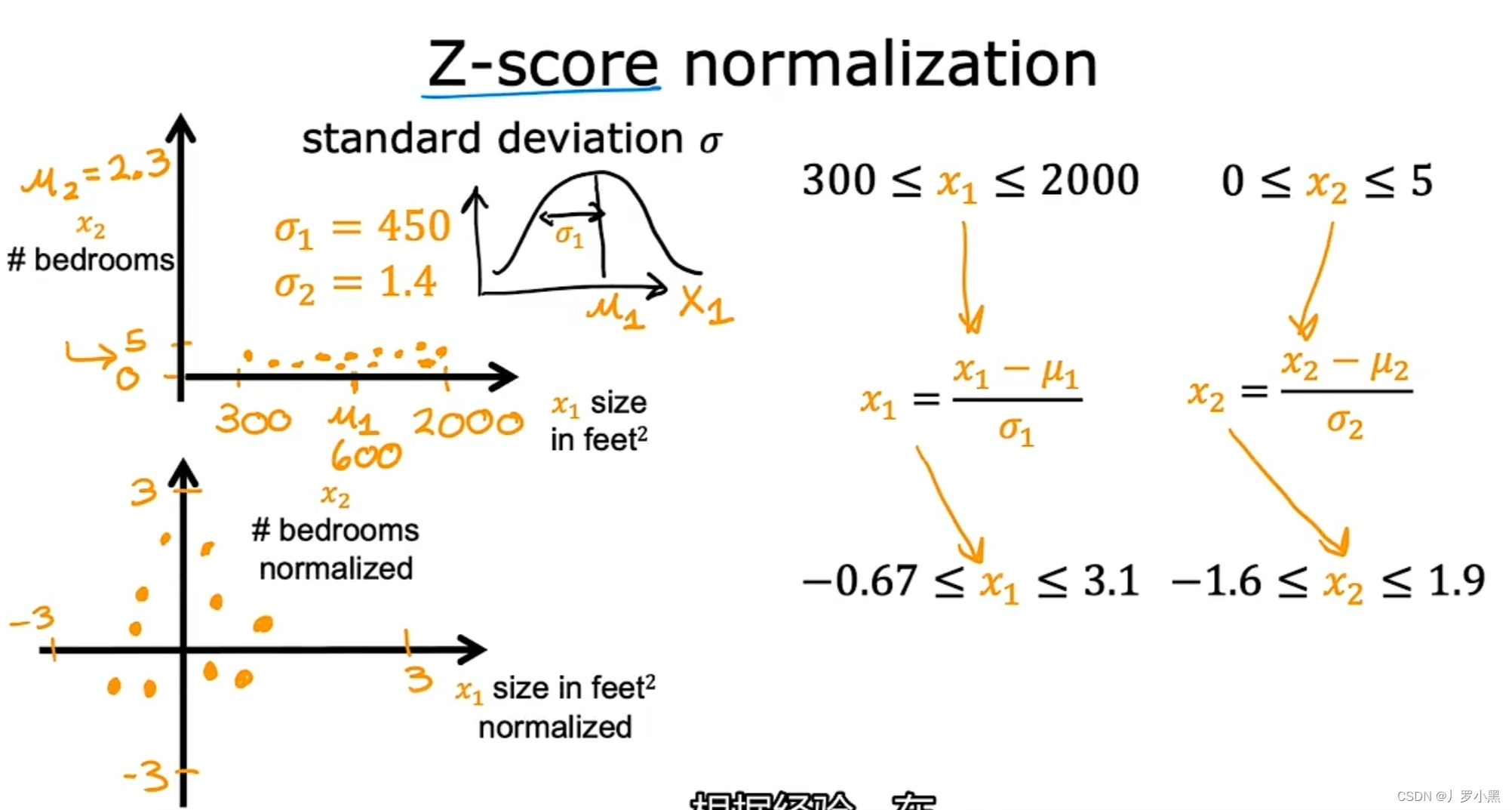
- Z-score 标准化:
- 步骤:先计算某特征的标准差和平均值,再将该特征的可能值减该特征的平均值,除以该特征的标准差。如图: