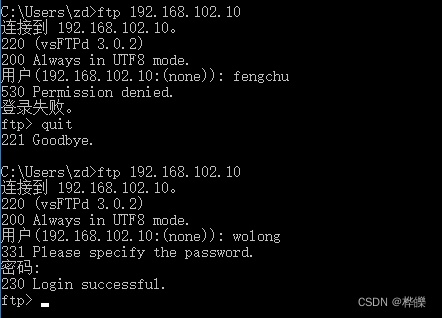
一、前言

上篇我们提到了,如果在光线追踪中,我们真的用每个像素发出的光线,以及在场景中弹射之后的光线与场景中的许多模型的上千万个三角形求交那将是一个非常慢的计算过程,所以,本篇我们将介绍一些加速结构来加速这个过程。
二、Axis-Aligned Bounding Box (AABB)—轴对齐包围盒
1.Bounding Volumes—包围盒

包围盒是一种加速结构中常用的做法,对于任意一个复杂的形状,我们都用一个简单的形状把它包围起来,如上图中的茶壶被矩形/圆形包围,而空间中的模型也是一样。这里面的思想是,如果光线连包围盒都碰不到,那就更不可能碰到包围内的物体了。
2.轴对齐包围盒(AABB)

在实际情况中我们经常用到的是轴对齐包围盒,意思就是说这个包围盒的6个面都是和三维空间的坐标轴对齐的,它们分别和XOY,YOZ,XOZ平面平行。这样做的目的是方便后面的计算。

我们先以二维情况作为例子说明,假设平面空间中有一个二维的包围盒,然后我们仍然用光线o+td先和包围盒的与y轴平行的x0和x1面求交,我们可以得到光线进入到达x0的时间tmin,从x1出去的时间tmax,同样的我们对y0,y1两个面做同样的运算也可以得到两个t值,那么光线在包围盒中的是那一段呢?显然我们对左,中两幅图求交就是最右面的图,也就是光线进入包围盒和出去包围盒的时间。为什么会这样呢?我们说,轴对齐包围盒本身就是坐标轴的面求交得到的一个空间,那么光线在这片空间中的时间自然也就是进出各个面的光线时间求交。

根据上面的结论我们推广到三维空间,无非就是多了一个面,那么什么时候光线进入了盒子呢?很简单,当光线进入了所有的面,就说明光线进入了盒子,而光线离开任意一个面,就说明光线离开了盒子。所以光线进入盒子的时间就是光线进入三个面时间中的最大值,而光线离开盒子的时间就是光线离开三个面时间中的最小值。而如果求出的进入盒子时间<离开盒子时间,也就说明光线进在盒子里面待了一段时间,也就是和包围盒有交点。

那么负值如何考虑呢?首先光线不是直线,是一条射线,所以我们要考虑正负。分几种情况:
首先如果进入时间和离开时间都>0,那么说明盒子是在光线起点的背后,也就一定没有交点。
其次如果进入时间<0,而离开时间>0,那么说明光线的出发点o在盒子里面,也就一定有交点。
那么也就说明,当且仅当进入时间<离开时间且离开时间>0的时候,光线与包围盒才有交点。

最后解释一下为什么轴对齐包围盒容易计算,我们前面提到过光线与平面求交的计算,而这是通常情况,平面不一定与坐标轴对齐。而如果我们使用轴对齐的特性,如上图的第二幅图中,我们可以直接用水平分量x计算光线与平面相交的时间t,这会简便很多。
三、Uniform Spatial Partitions(Grids)—均匀空间划分

紧接着我们的AABB,我们来说包围盒中和光线的具体运算过程,首先对于上面的物体,我们先找到一个包围盒,然后均匀的划分空间成很多小格子,然后找到哪些格子里面有物体,这是在做预处理。

在预处理之后,我们就可以对光线进行求交计算了,如果在一个小格子中既有物体又有光线,那么说明光线和物体可能有交点,就在这个格子里进行光线与物体表面的求交计算,否则就不会计算。那么我们怎么知道光线穿过了哪些格子呢?要一个一个进行求交计算吗?实际上是不需要的,这里其实可以用到光栅化直线的算法,如引入增量运算的Bresenham算法等,感兴趣的朋友可以自行了解。

那么格子划分的疏密怎么确定呢?划分的如果太稀疏,假如不划分,只用一个大包围盒,那相当于没有加速结构,而如果划分的太密集我们又要多次计算光线与小网格的求交。而经过不断的尝试人们发现,划分网格的数量应该等于某一个常数C乘上场景中物体的数量。
四、Spatial Partitions—空间划分

在上面提到的均匀空间划分中,我们会碰到很多问题,假如在一个很空旷的操场中放置了一个茶壶,那么我们需要先用一个很大很大的包围盒把操场包起来,然后在里面划分好多好多格子,然后光线与许多格子求交最后才能找到这个茶壶。也就是说在物体没那么多的地方,我们不需要划分很多格子,直接用一个大格子就可以了,而物体密集的地方格子划分的密集一些就好了。而改进后的方法就是Spatial Partitions—空间划分。而划分结构也分很多种,包括Oct-Tree(八叉树),KD-Tree(KD树),BSP-Tree(二叉空间划分树)。在这里我们主要介绍KD-Tree,原因是KD-Tree在高维仍然很好用,而像八叉树在二维空间中是四叉树,三维空间是八叉树,更高维的空间就变成了2的n次方叉树。而BSP树,在二维空间我们是用线划分,三维空间用平面划分,而高维空间我们则需要用超平面划分,也很麻烦。而KD树的做法是各个维度按顺序依次划分,先对着x划分,然后y,然后z,然后再xyz,如果更高维度就变成xyzw循环,每次对空间划分只划分两个区域。

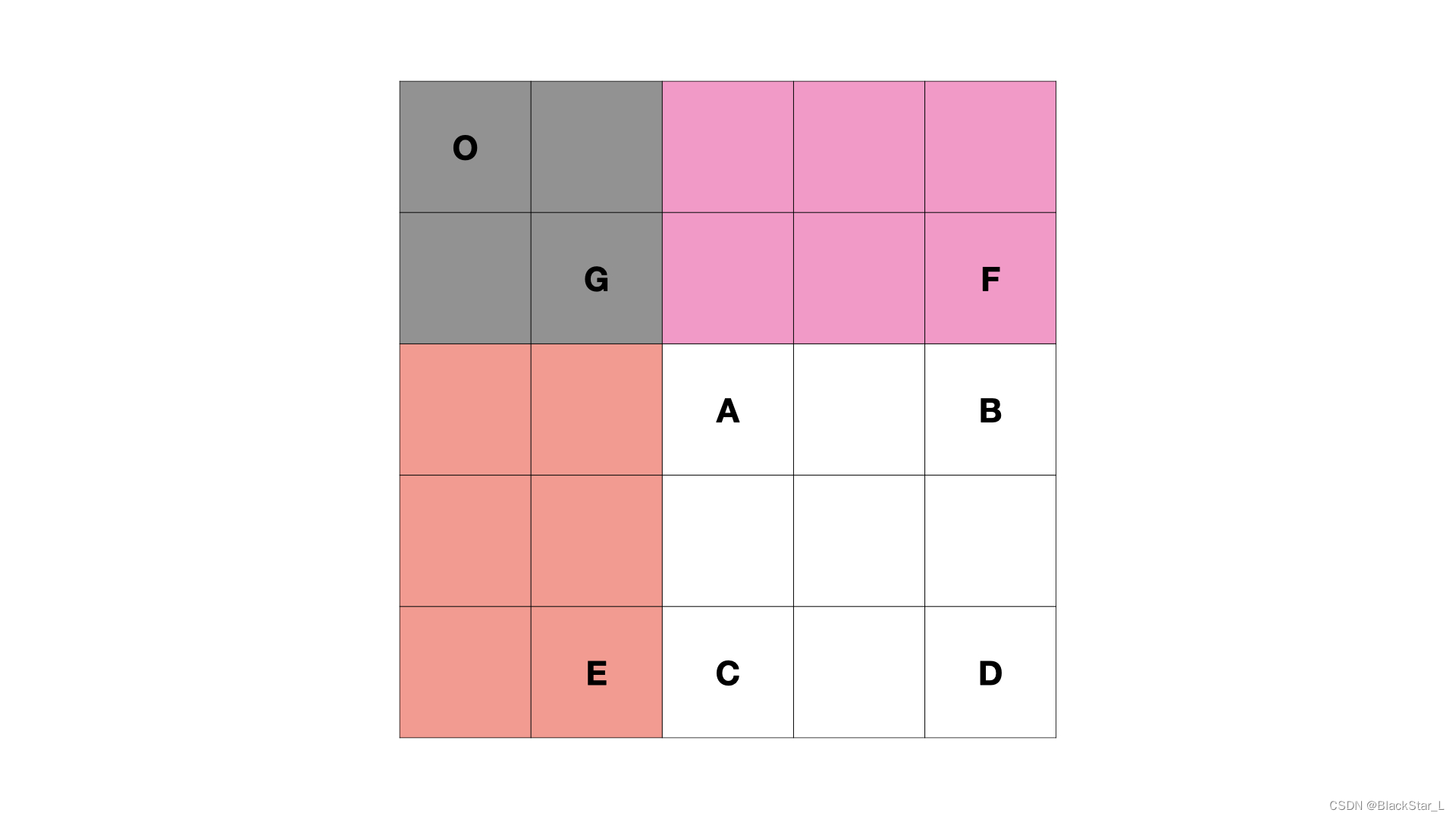
而正是因为我们每次都只把空间划成两块区域,我们自然可以用二叉树来存储这一加速结构。同样的,KD树也是在我们做光线追踪前对包围盒的预处理。与此同时,中间节点A,B,C,D并不存储任何对象,而对象物体都存储在叶子节点中。

和之前的均匀网格一样,我们对KD树划分的区域也同样需要进行求交。在预处理完包围盒之后,我们就可以对划分的区域进行求交了,步骤如上图所示,先对A求交,发现与A有交点,那么就要对A的子节点也进行求交,因为1没有继续划分,所以对1内的物体进行求交,再对B节点求交,然后沿着子节点依次这么做,最后对C节点的子节点3内的物体求交时成功找到了光线与物体的交点。
当然KD-Tree也有它的问题,例如,我们怎么判断一个立方体格子和一个三角形求交。其次一个物体可能会被存储在很多不同的格子里,这显然加大了复杂程度。
五、Object Partitions & Bounding Volume Hierarchy(BVH)—对象分区&边界体积层次


针对上面KD-Tree存在的问题,人们又发明了一种划分方法,只不过这次划分的并不是空间,而是划分物体。如果我们有一堆三角形如上图,我们把这堆三角形分为两部分,然后分别求它们的包围盒,这两部分作为最初节点的两个子节点,然后再对下面的子节点用同样的方法划分它们,也是重新求出它们的包围盒,递归下去,直到叶子节点中的三角形足够少的时候停下来。同样中间节点只存包围盒与子节点的指针,只有叶子节点存储物体。用这种方法我们同样可以建立起一个树结构,而且有效避免了KD-Tree中一个三角形出现在多个节点中的问题。
当然BVH也有它的问题,如这些重新划分的包围盒之间会有重合,当然重合的影响并不是致命的,只要划分的重合度导致的误差过大以至于发生错误。所以怎么划分也是一个很难研究的问题。

为了均匀划分,我们通常每次都沿着最长的轴划分,从而保证包围盒不过于“细长”或者“矮扁”。
如何把物体分成两半呢?人们通常取处在中间位置的物体来划分,这样可以保证两部分的物体数量差不多,也就可以使得构建的树结构的最大深度最小,也就是树两个叉的深度平衡。而这本质是一个取中位数的问题,在n个数中快速取得第i大的数实际上是一个快速选择算法,时间复杂度是O(n),感兴趣的朋友可以自行了解。

光线与BVH求交的伪码
光线和BVH的求交并没有本质区别,也就是包围盒加速结构的应用本质上都是类似的,同样的我们做光线与包围盒的求交,如果与父节点有交点,则计算与其它两个子节点的求交,如果子节点是叶子节点则计算光线与叶子节点内物体的求交,否则继续计算子节点的子节点,如此递归的算法。
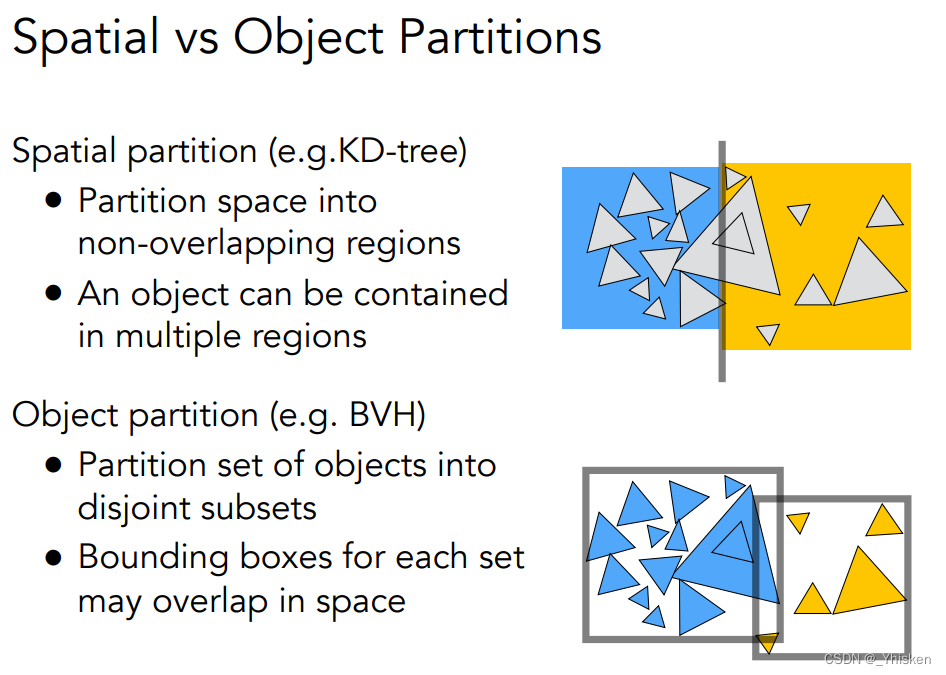
最后做一下比较,对于KD-Tree,它是对空间划分,并且一个物体可能被存储在不同的区域。而对于BVH,则是对对象进行划分,并且它们重新划分的区域可能会重叠。
六、总结
到这里整个Whitted-Style光线追踪以及包围盒的加速结构和求交算法就都介绍完了,下节课我们进入辐射度量学,是一种更现代,效果也更好的方法。
参考:
Lecture 13 Ray Tracing 1_哔哩哔哩_bilibili
Lecture 14 Ray Tracing 2_哔哩哔哩_bilibili
GAMES101_Lecture_13 (ucsb.edu)
GAMES101_Lecture_14 (ucsb.edu)