算法总结8 前缀和

一、前缀和的概念
- 1.1、什么是前缀和？
- 1.2、常见类型
- - 1.2.1、求数组前i个数之和
  - 1.2.2、求数组的区间和
二、经典例题
- - 2.1、求数组前i个数之和
  - - 560. 和为 K 的子数组 - 前缀和+哈希表
    - 525. 连续数组
  - 2.2、求数组的区间和
  - - 303. 区域和检索 - 数组不可变
    - 643. 子数组最大平均数 I - （隐藏的前缀和）
    - 304. 二维区域和检索 - 矩阵不可变 - （二维区间）
参考

在这里插入图片描述

一、前缀和的概念

1.1、什么是前缀和？

前缀和，英文是 preSum。是面试中经常考到的题目，并且难度也不大，我们直接从题目入手开始讲解。

首先我们看看一道很经典的简单题 1480. 一维数组的动态和，在没接触过前缀和的时候，我们对这道题的解法，很可能采用双重循环：

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        preSum = []
        # 选取每一个索引，当做下一层循环的结尾
        for i in range(len(nums)):
            # 用来记录总和
            su_m = 0
            # 从0开始到i求和
            for j in range(i+1):
                su_m+=nums[j]
            # 添加到结果
            preSum.append(su_m)
        return preSum

又或者我们取消内层循环，直接sum对切片求和与存储：

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        preSum = []
        # 选取每一个索引，当做下一层循环的结尾
        for i in range(len(nums)):
            # 用sum函数对切片求和
            preSum.append(sum(nums[:i+1]))
        return preSum

这种直接求和是很简单直接的，但是它的效率是非常低的，因为我们没有利用到一个条件，也就是值之间的关系，即preSum的第i个值取决于第i-1个值：

输入：nums = [1,2,3,4]
输出：[1,3,6,10]
解释：动态和计算过程为 [1, 1+2, 1+2+3, 1+2+3+4] 。

1 这个值的索引为第一个，前面没有值，直接等于当前nums的1
1+2 = 前一个1 加上当前的nums上的2
1+2+3 = 前一个1+2 加上当前nums上的3
1+2+3+4 = 前一个1+2+3 加上当前nums上的4

有了这个规律我们可以很轻易的写出：

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
        for i in range(1, len(nums)):
            nums[i] = nums[i]+nums[i-1]
        return nums

我们可以写的更加规范一点：

class Solution:
    def runningSum(self, nums: List[int]) -> List[int]:
    	# 使用新数组去存储结果
    	preSum = []
    	# 把索引0加入其中
        for i in range(len(nums)):
        	if i==0:
        		preSum.append(nums[i)
        	else:
            	nums[i] = nums[i]+preSum[i-1]
        return nums

如果理解了上面的内容，那么我告诉你，preSum 数组其实就是「前缀和」。

「前缀和」是从 nums 数组中的第 0 位置开始累加，到第 i 位置的累加结果，我们常把这个结果保存到数组 preSum 中，记为 preSum[i]。

在前面计算「前缀和」的代码中，计算公式为 preSum[i] = preSum[i - 1] + nums[i] ，为了防止当 i = 0 的时候数组越界，所以加了个 if (i == 0) 的判断，即 i == 0 时让 preSum[i] = nums[i]。

在其他常见的写法中，为了省去这个 if 判断，我们常常把「前缀和」数组 preSum 的长度定义为原数组的长度 + 1。preSum 的第 0 个位置，相当于一个占位符，置为 0。
那么就可以把 preSum 的公式统一为 preSum[i] = preSum[i - 1] + nums[i - 1]，此时的preSum[i]表示nums中 i 元素左边所有元素之和（不包含当前元素 i）。

下面以 [1, 12, -5, -6, 50, 3] 为例，用动图讲解一下如何求 preSum：

请添加图片描述
上图表示：
preSum[0] = 0;
preSum[1] = preSum[0] + nums[0];
preSum[2] = preSum[1] + nums[1];
…

1.2、常见类型

一般分为两种类型：

类型一	类型二
求数组前 i 个数之和	求数组的区间和

1.2.1、求数组前i个数之和

求数组前 i 个数之和，是「前缀和」数组的定义，所以是最基本的用法。
举例而言：

如果要求 nums 数组中的前2个数的和，即sum(nums[0], nums[1])，直接返回 preSum[2]即可
同理，如果要求 nums 数组中所有元素的和，即sum(nums[0], …, nums[length-1])，直接返回preSum[length]即可

1.2.2、求数组的区间和

利用 preSum 数组，可以在 O(1) 的时间内快速求出 nums 任意区间 [i,j] (两端都包含) 内的所有元素之和。

公式为：sum(i,j) = preSum[j+1] - preSum[i]

什么原理呢？其实就是消除公共部分，即0-i-1部分的和，那么就能得到 i-j 部分的区间和。

注意上面的式子，使用的是 preSum[j+1] 和preSum[i]：

preSum[j+1] 表示的是 nums 数组中 [0, j] 的所有数字之和（包含0和j）
preSum[i] 表示的是 nums 数组中[0, i-1]的所有数字之和（包含0和i-1）
两者相减时，结果留下了 nums 数组中 [i, j] 的所有数字之和

二、经典例题

2.1、求数组前i个数之和

560. 和为 K 的子数组 - 前缀和+哈希表

560. 和为 K 的子数组

from collections import defaultdict
class Solution:
    def subarraySum(self, nums: List[int], k: int) -> int:
        preSum = defaultdict(int)
        preSum[0]=1
        presum = 0
        count=0
        for i in range(len(nums)):
            presum+=nums[i]
            
            count+=preSum[presum-k]
            preSum[presum]+=1
        return count

525. 连续数组

我们以nums的前缀和来构造一个hashmap，并且该hashmap不能改变，只能增加（保留第一次出现的index，第二次出现则做ans的max保留），因为它是记录第一次出现的位置，当第二次出现key时则做相应索引的减法，即为结果长度，该长度中0和1数量相同，举例说明：
0 1 0 0 1 0
-1 0 -1 -2 -1

index	nums	pre_sum	hashmap{0:-1}	ans
0	0	-1	hashmap找不到-1，增加：{0:-1, -1:0}	0
1	1	0	hashmap能找到0，求ans	1-(-1)=2
2	0	-1	hashmap能找到-1，求ans	2-0=2
3	0	-2	hashmap找不到-2，增加：{0:-1, -1:0, -2:3}	2（保留最大值）
4	1	-1	hashmap能找到-1，求ans	4-0=4
5	0	-2	hashmap能找到-2，求ans	5-3=2, 但4（保留最大值）

思考：为什么第二次出现的值，即便不是0，而是-1或-2，也都能计算ans？
第二次出现说明这两个值之间的累加和为0，也就是0和1数量相等，我们需要关注的是两个前缀和的差值之间的累加和是否为0，而不是只看前缀和的值，这是无意义的，因为前缀和只能代表该值前面所有值累加的特征值。

class Solution:
    def findMaxLength(self, nums: List[int]) -> int:
        # 前缀和字典: key为1的数量和0的数量的差值,value为对应坐标
        hashmap = {0:-1}
        # 当前1的数量和0的数量的差值
        ans = pre_sum = 0

        for i,num in enumerate(nums):
            # 每多一个1，差值+1，每多一个0，差值-1
            pre_sum+=1 if num else -1
            # 如果存在1和0的数量差值相等的地方，那么说明后者到前者之前1和0的数量相等！
            if pre_sum in hashmap:
                ans = max(ans, i-hashmap[pre_sum])
            # 在hashmap里面就进行比较，不在则存储
            else:
                hashmap[pre_sum]=i
        return ans

2.2、求数组的区间和

在这里插入图片描述

303. 区域和检索 - 数组不可变

通过 1.2.2、求数组的区间和 的内容可以秒杀这道题。

class NumArray:

    def __init__(self, nums: List[int]):
        self.preSum = [0]
        for i in range(len(nums)):
            self.preSum.append(self.preSum[i]+nums[i]) 

    def sumRange(self, left: int, right: int) -> int:
        return self.preSum[right+1]-self.preSum[left]

# Your NumArray object will be instantiated and called as such:
# obj = NumArray(nums)
# param_1 = obj.sumRange(left,right)

643. 子数组最大平均数 I - （隐藏的前缀和）

643. 子数组最大平均数 I
这道题可以用前缀和解，也可以用固定大小为k的滑动窗口来解决

解法1：前缀和:
要求大小为k的窗口内的最大平均数，可以求[i, i+k]区间的最大和再除以k，即要求(preSum[i+k]- preSum[i])/k 的最大值。总之题目要求 区间和 的时候，那么就可以考虑使用前缀和。

class Solution:
    def findMaxAverage(self, nums: List[int], k: int) -> float:
        preSum = [0]
        for i in range(len(nums)):
            preSum.append(preSum[i]+nums[i])
        max_avg = -float('inf')
        for i in range(len(nums)-k+1):
            max_avg = max(max_avg, (preSum[i+k]-preSum[i])/k)
        return max_avg

解法二：滑动窗口
滑动窗口类型的题解思路可以看看这篇文章：算法刷题总结 (七) 双指针

class Solution:
    def findMaxAverage(self, nums: List[int], k: int) -> float:
        left,right = 0, k-1
        avg = sum(nums[left:right+1])
        max_avg = avg
        for i in range(k, len(nums)):
            avg+=nums[i]-nums[i-k]
            max_avg = max(avg, max_avg)
        return max_avg/k

在这里插入图片描述

304. 二维区域和检索 - 矩阵不可变 - （二维区间）

304. 二维区域和检索 - 矩阵不可变

当「前缀和」拓展到二维区间时，可以用下面的思路求解：

（1）步骤一：求 preSum
我们定义 $p re S u m [i + 1] [j + 1]$ ，即同前面，row与col都增加一位。第一行和第一列为占位符，值为0。从 $[1] [1]$ 到 $[ro w + 1] [co l + 1]$ 表示矩阵 $ma t r i x [0] [0]$ 到 $[ro w] [co l]$ 的前缀面积和。

递推公式为：
$p re S u m [i + 1] [j + 1] = p re S u m [i] [j + 1] + p re S u m [i + 1] [j] - p re S u m [i] [j] + ma t r i x [i] [j]$

可以用下图帮助理解：
$S (O, D) = S (O, C) + S (O, B) - S (O, A) + D$

在这里插入图片描述
减去 $S (O, A)$ 的原因是 $S (O, C)$ 和 $S (O, B)$ 中都有 $S (O, A)$ ，即加了两次 $S (O, A)$ ，所以需要减去一次 $S (O, A)$ 。

<br

（2）步骤二：根据 preSum 求子矩阵面积

前面已经跟你求出了数组从 $[0, 0]$ 位置到 $[i, j]$ 位置的 $p re S u m$ 。

如果要求 $[ro w 1, co l 1]$ 到 $[ro w 2, co l 2]$ 的子矩阵的面积的话，用 preSum计算时，对应了以下的递推公式：
$p re S u m [ro w 2 + 1] [co l 2 + 1] - p re S u m [ro w 2 + 1] [co l 1] - p re S u m [ro w 1] [co l 2 + 1] + p re S u m [ro w 1] [co l 1]$ 。

同样利用一张图来说明：

$S (A, D) = S (O, D) - S (O, E) - S (O, F) + S (O, G)$

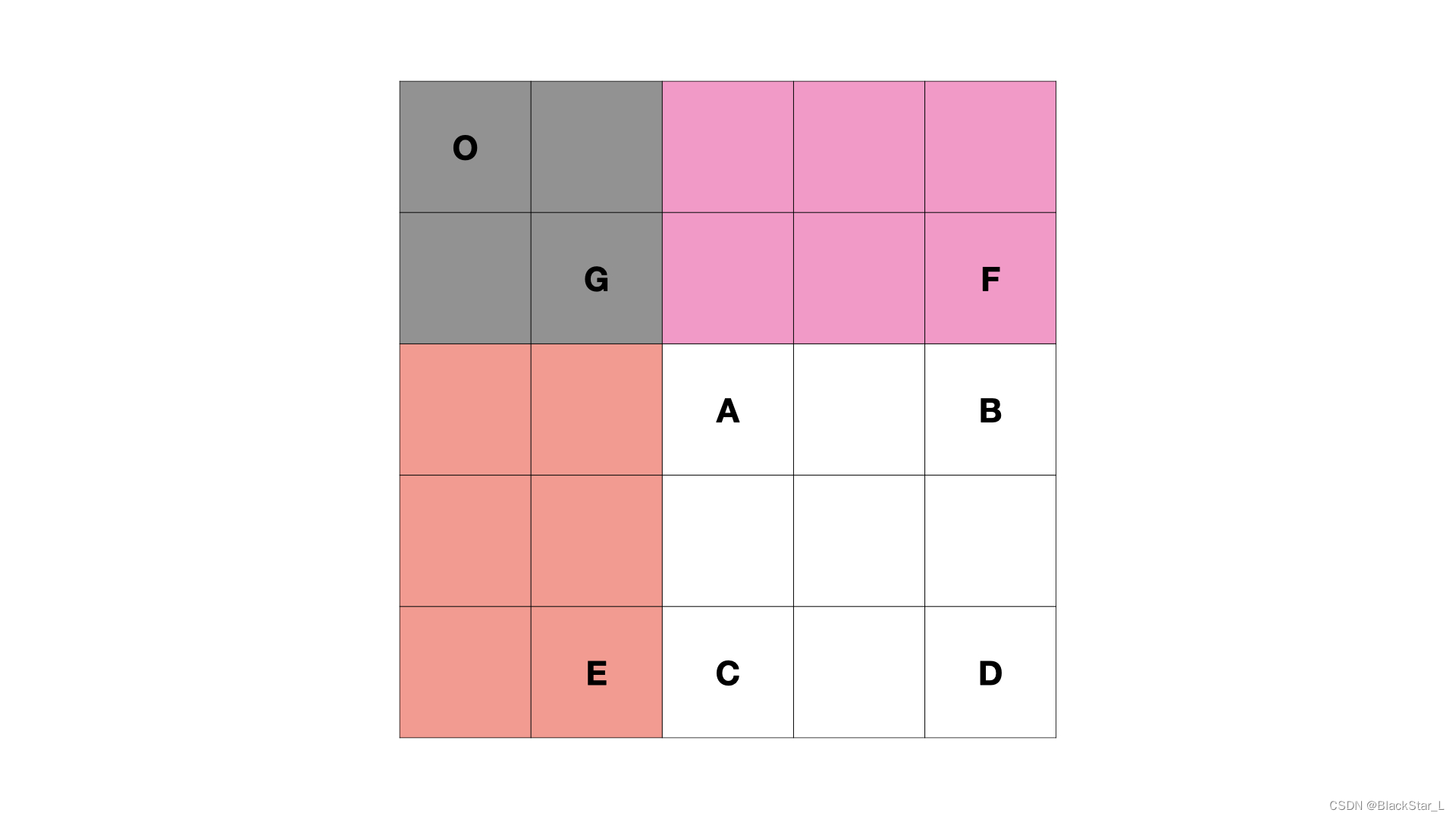
在这里插入图片描述
加上子矩阵 $S (O, G)$ 面积的原因是 $S (O, E)$ 和 $S (O, F)$ 中都有 $S (O, G)$ ，即减了两次 $S (O, G)$ ，所以需要加上一次 $S (O, G)$ 。

整理清楚后，整体的代码如下：

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        row, col = len(matrix), len(matrix[0])
        self.preSum = [[0]*(col+1) for _ in range(row+1)]
        for i in range(row):
            for j in range(col):
                self.preSum[i+1][j+1] = self.preSum[i][j+1]+self.preSum[i+1][j]-self.preSum[i][j]+matrix[i][j]

    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.preSum[row2+1][col2+1]-self.preSum[row2+1][col1]-self.preSum[row1][col2+1]+self.preSum[row1][col1]




# Your NumMatrix object will be instantiated and called as such:
# obj = NumMatrix(matrix)
# param_1 = obj.sumRegion(row1,col1,row2,col2)