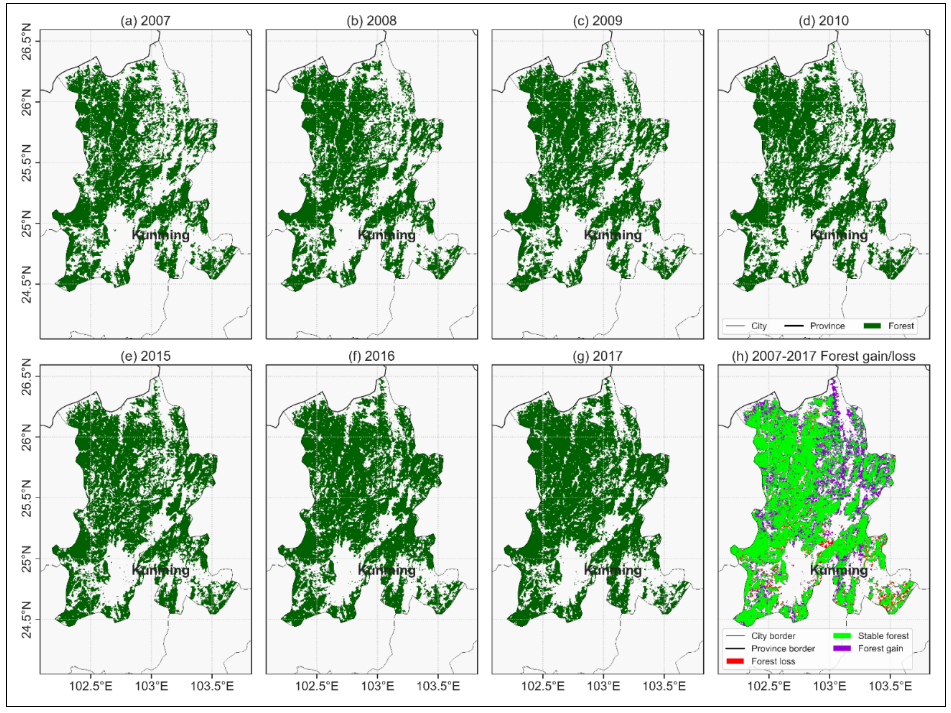
TreeMap是基于红黑树(Red-Black tree)的 NavigableMap 实现(是自平衡的二叉树)。该映射根据其键的自然顺序进行排序,或者根据创建映射时提供的 Comparator 进行排序,具体取决于使用的构造方法。
一、对外开放API
TreeMap提供了保证log(n)时间成本containsKey , get , put和remove操作。 算法是对Cormen,Leiserson和Rivest的算法导论中的算法的改编。
请注意,如果此有序映射要正确实现Map接口,则树映射维护的排序(如任何已排序的映射,以及是否提供显式比较器)必须与equals一致 。
请注意,此实现不同步。 如果多个线程同时访问映射,并且至少有一个线程在结构上修改了映射,则必须在外部进行同步。 如果不存在此类对象,则应使用Collections.synchronizedSortedMap方法“包装”地图。
| 变量和类型 | 方法 | 描述 |
| Map.Entry<K,V> | ceilingEntry(K key) | 返回与大于或等于给定键的最小键关联的键 - 值映射,如果没有此键,则 null 。 |
| K | ceilingKey(K key) | 返回大于或等于给定键的 null键,如果没有这样的键,则 null 。 |
| void | clear() | 从此映射中删除所有映射。 |
| Object | clone() | 返回此 TreeMap实例的浅表副本。 |
| boolean | containsKey(Object key) | 如果此映射包含指定键的映射,则返回 true 。 |
| boolean | containsValue(Object value) | 如果此映射将一个或多个键映射到指定值,则返回 true 。 |
| NavigableSet<K> | descendingKeySet() | 返回此映射中包含的键的反向顺序NavigableSet视图。 |
| NavigableMap<K,V> | descendingMap() | 返回此映射中包含的映射的逆序视图。 |
| Set<Map.Entry<K,V>> | entrySet() | 返回此映射中包含的映射的Set视图。 |
| Map.Entry<K,V> | firstEntry() | 返回与此映射中的最小键关联的键 - 值映射,如果映射为空,则 null 。 |
| K | firstKey() | 返回此映射中当前的第一个(最低)键。 |
| Map.Entry<K,V> | floorEntry(K key) | 返回与小于或等于给定键的最大键关联的键 - 值映射,如果没有此键,则 null 。 |
| K | floorKey(K key) | 返回小于或等于给定键的最大键,如果没有这样的键,则 null 。 |
| V | get(Object key) | 返回指定键映射到的值,如果此映射不包含键的映射,则返回 null 。 |
| SortedMap<K,V> | headMap(K toKey) | 返回此映射的部分视图,其键严格小于 toKey 。 |
| NavigableMap<K,V> | headMap(K toKey, boolean inclusive) | 返回此映射的部分视图,其键小于(或等于,如果 inclusive为真) toKey 。 |
| Map.Entry<K,V> | higherEntry(K key) | 返回与严格大于给定键的最小键关联的键 - 值映射,如果没有此键,则 null 。 |
| K | higherKey(K key) | 返回严格大于给定键的最小键,如果没有这样的键,则返回 null 。 |
| Set<K> | keySet() | 返回此映射中包含的键的Set视图。 |
| Map.Entry<K,V> | lastEntry() | 返回与此映射中的最大键关联的键 - 值映射,如果映射为空,则 null 。 |
| K | lastKey() | 返回此映射中当前的最后一个(最高)键。 |
| Map.Entry<K,V> | lowerEntry(K key) | 返回与严格小于给定键的最大键相关联的键 - 值映射,如果没有这样的键,则 null 。 |
| K | lowerKey(K key) | 返回严格小于给定键的最大键,如果没有这样键,则返回 null 。 |
| NavigableSet<K> | navigableKeySet() | 返回此映射中包含的键的NavigableSet视图。 |
| Map.Entry<K,V> | pollFirstEntry() | 删除并返回与此映射中的最小键关联的键 - 值映射,如果映射为空,则 null 。 |
| Map.Entry<K,V> | pollLastEntry() | 删除并返回与此映射中的最大键关联的键 - 值映射,如果映射为空,则 null 。 |
| V | put(K key, V value) | 将指定的值与此映射中的指定键相关联。 |
| void | putAll(Map<? extends K,? extends V> map) | 将指定映射中的所有映射复制到此映射。 |
| V | remove(Object key) | 如果存在,则从此TreeMap中删除此键的映射。 |
| int | size() | 返回此映射中键 - 值映射的数量。 |
| NavigableMap<K,V> | subMap(K fromKey, boolean fromInclusive, K toKey, boolean toInclusive) | 返回此映射部分的视图,其键范围为 fromKey至 toKey 。 |
| SortedMap<K,V> | subMap(K fromKey, K toKey) | 返回此映射部分的视图,其键的范围从 fromKey (包括 toKey )到 toKey (独占)。 |
| SortedMap<K,V> | tailMap(K fromKey) | 返回此映射的部分视图,其键大于或等于 fromKey 。 |
| NavigableMap<K,V> | tailMap(K fromKey, boolean inclusive) | 返回此映射的部分视图,其键大于(或等于,如果 inclusive为真) fromKey 。 |
二、TreeMap构造
我们先看一下TreeMap中主要的成员变量
/**
* 我们前面提到TreeMap是可以自动排序的,默认情况下comparator为null,这个时候按照key的自然顺序进行排
* 序,然而并不是所有情况下都可以直接使用key的自然顺序,有时候我们想让Map的自动排序按照我们自己的规则,
* 这个时候你就需要传递Comparator的实现类
*/
private final Comparator<? super K> comparator;
/**
* TreeMap的存储结构既然是红黑树,那么必然会有唯一的根节点。
*/
private transient Entry<K,V> root;
/**
* Map中key-val对的数量,也即是红黑树中节点Entry的数量
*/
private transient int size = 0;
/**
* 红黑树结构的调整次数
*/
private transient int modCount = 0;上面的主要成员变量根节点root是Entry类的实体,我们来看一下Entry类的源码:
static final class Entry<K,V> implements Map.Entry<K,V> {
//key,val是存储的原始数据
K key;
V value;
//定义了节点的左孩子
Entry<K,V> left;
//定义了节点的右孩子
Entry<K,V> right;
//通过该节点可以反过来往上找到自己的父亲
Entry<K,V> parent;
//默认情况下为黑色节点,可调整
boolean color = BLACK;
/**
* 构造器
*/
Entry(K key, V value, Entry<K,V> parent) {
this.key = key;
this.value = value;
this.parent = parent;
}
/**
* 获取节点的key值
*/
public K getKey() {return key;}
/**
* 获取节点的value值
*/
public V getValue() {return value;}
/**
* 用新值替换当前值,并返回当前值
*/
public V setValue(V value) {
V oldValue = this.value;
this.value = value;
return oldValue;
}
public boolean equals(Object o) {
if (!(o instanceof Map.Entry))
return false;
Map.Entry<?,?> e = (Map.Entry<?,?>)o;
return valEquals(key,e.getKey()) && valEquals(value,e.getValue());
}
public int hashCode() {
int keyHash = (key==null ? 0 : key.hashCode());
int valueHash = (value==null ? 0 : value.hashCode());
return keyHash ^ valueHash;
}
public String toString() {
return key + "=" + value;
}
}Entry静态内部类实现了Map的内部接口Entry,提供了红黑树存储结构的java实现,通过left属性可以建立左子树,通过right属性可以建立右子树,通过parent可以往上找到父节点。
三、红黑树
红黑树是一种近似平衡的二叉查找树,它能够确保任何一个节点的左右子树的高度差不会超过二者中较低那个的一倍。具体来说,红黑树是满足如下条件的二叉查找树(binary search tree):
- 每个节点要么是红色,要么是黑色。
- 根节点必须是黑色
- 红色节点不能连续(也即是,红色节点的孩子和父亲都不能是红色)。
- 对于每个节点,从该点至
null(树尾端)的任何路径,都含有相同个数的黑色节点。
在树的结构发生改变时(插入或者删除操作),往往会破坏上述条件3或条件4,需要通过调整使得查找树重新满足红黑树的约束条件。
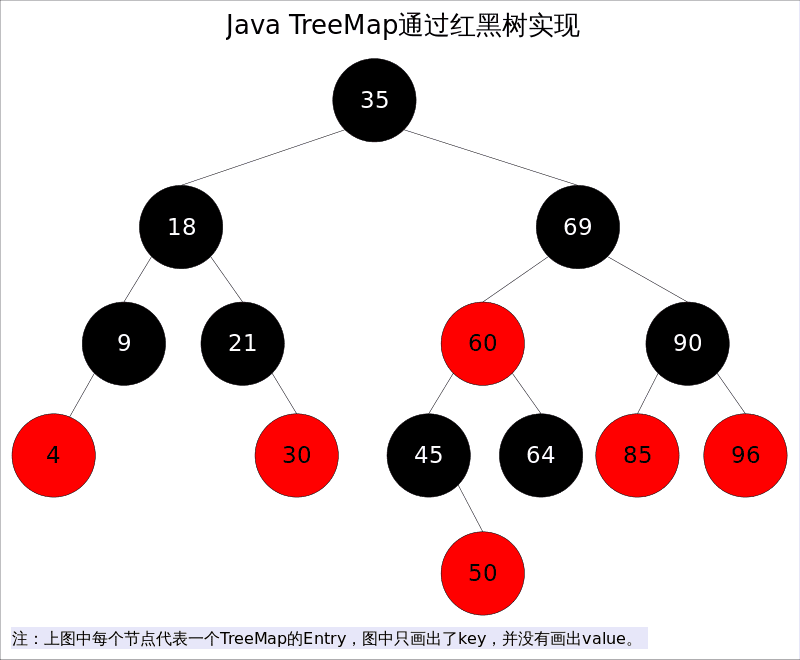
当查找树的结构发生改变时,红黑树的约束条件可能被破坏,需要通过调整使得查找树重新满足红黑树的约束条件。调整可以分为两类: 一类是颜色调整,即改变某个节点的颜色;另一类是结构调整,即改变检索树的结构关系。结构调整过程包含两个基本操作** : 左旋(Rotate Left),右旋(RotateRight)**。
1、左旋
左旋的过程是将x的右子树绕x逆时针旋转,使得x的右子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足。
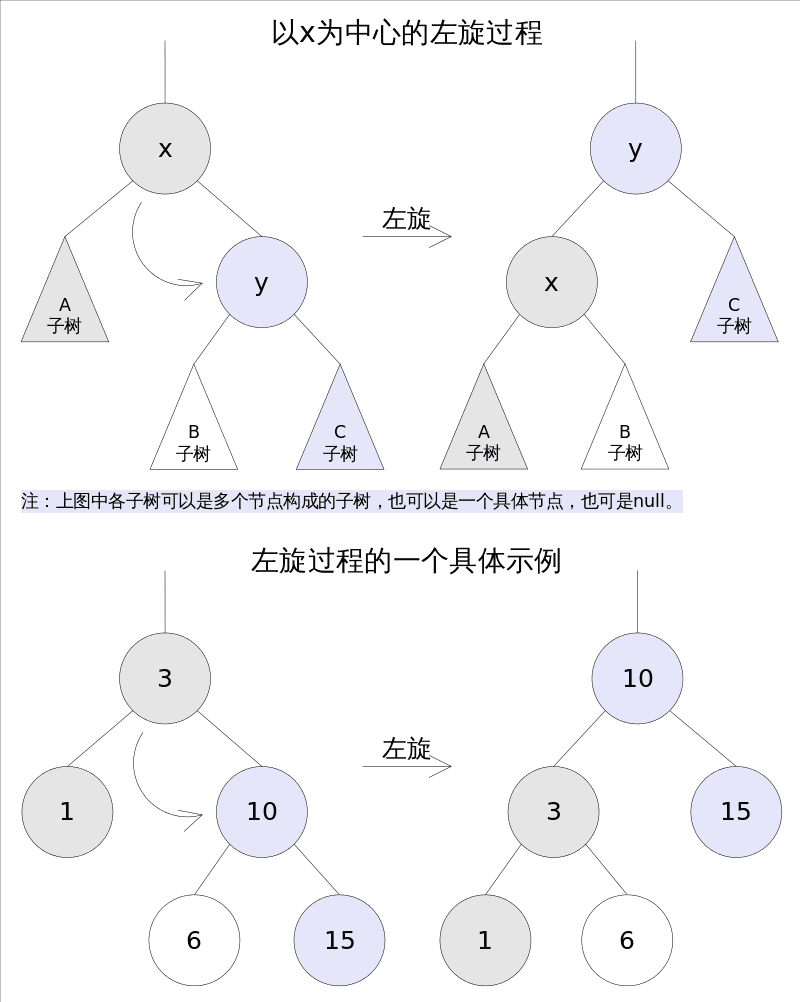
TreeMap中左旋代码如下:
//Rotate Left
private void rotateLeft(Entry<K,V> p) {
if (p != null) {
Entry<K,V> r = p.right;
p.right = r.left;
if (r.left != null)
r.left.parent = p;
r.parent = p.parent;
if (p.parent == null)
root = r;
else if (p.parent.left == p)
p.parent.left = r;
else
p.parent.right = r;
r.left = p;
p.parent = r;
}
}2、右旋
右旋的过程是将x的左子树绕x顺时针旋转,使得x的左子树成为x的父亲,同时修改相关节点的引用。旋转之后,二叉查找树的属性仍然满足。
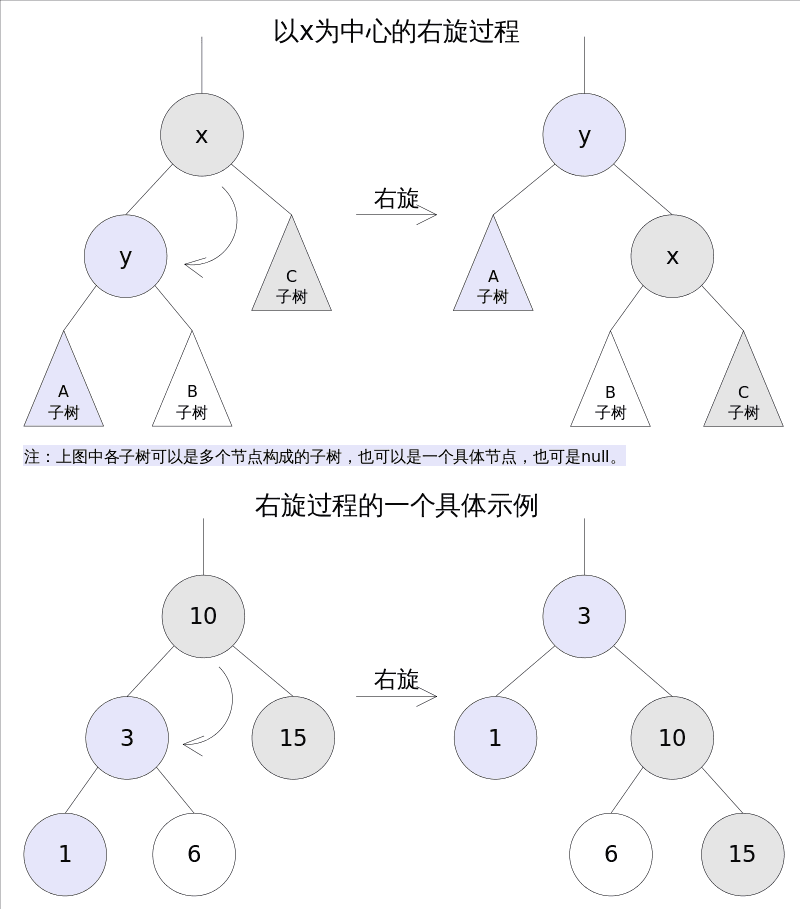
TreeMap中右旋代码如下:
//Rotate Right
private void rotateRight(Entry<K,V> p) {
if (p != null) {
Entry<K,V> l = p.left;
p.left = l.right;
if (l.right != null) l.right.parent = p;
l.parent = p.parent;
if (p.parent == null)
root = l;
else if (p.parent.right == p)
p.parent.right = l;
else p.parent.left = l;
l.right = p;
p.parent = l;
}
}四、方法剖析
1、get()
get(Object key)方法根据指定的key值返回对应的value,该方法调用了getEntry(Object key)得到相应的entry,然后返回entry.value。因此getEntry()是算法的核心。算法思想是根据key的自然顺序(或者比较器顺序)对二叉查找树进行查找,直到找到满足k.compareTo(p.key) == 0的entry。
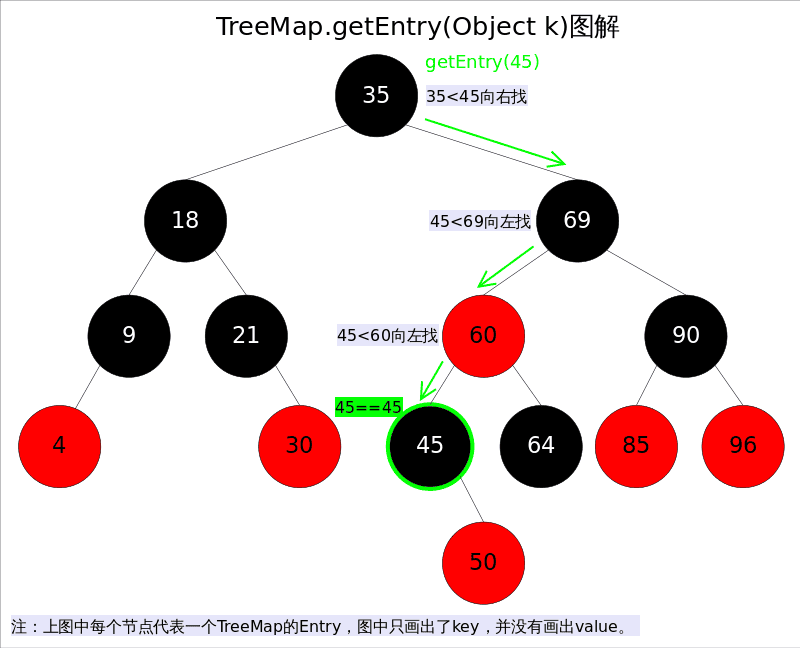
具体代码如下:
//getEntry()方法
final Entry<K,V> getEntry(Object key) {
......
if (key == null)//不允许key值为null
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然顺序
Entry<K,V> p = root;
while (p != null) {
int cmp = k.compareTo(p.key);
if (cmp < 0)//向左找
p = p.left;
else if (cmp > 0)//向右找
p = p.right;
else
return p;
}
return null;
}2、put()
put(K key, V value)方法是将指定的key, value对添加到map里。该方法首先会对map做一次查找,看是否包含该元组,如果已经包含则直接返回,查找过程类似于getEntry()方法;如果没有找到则会在红黑树中插入新的entry,如果插入之后破坏了红黑树的约束条件,还需要进行调整(旋转,改变某些节点的颜色)。
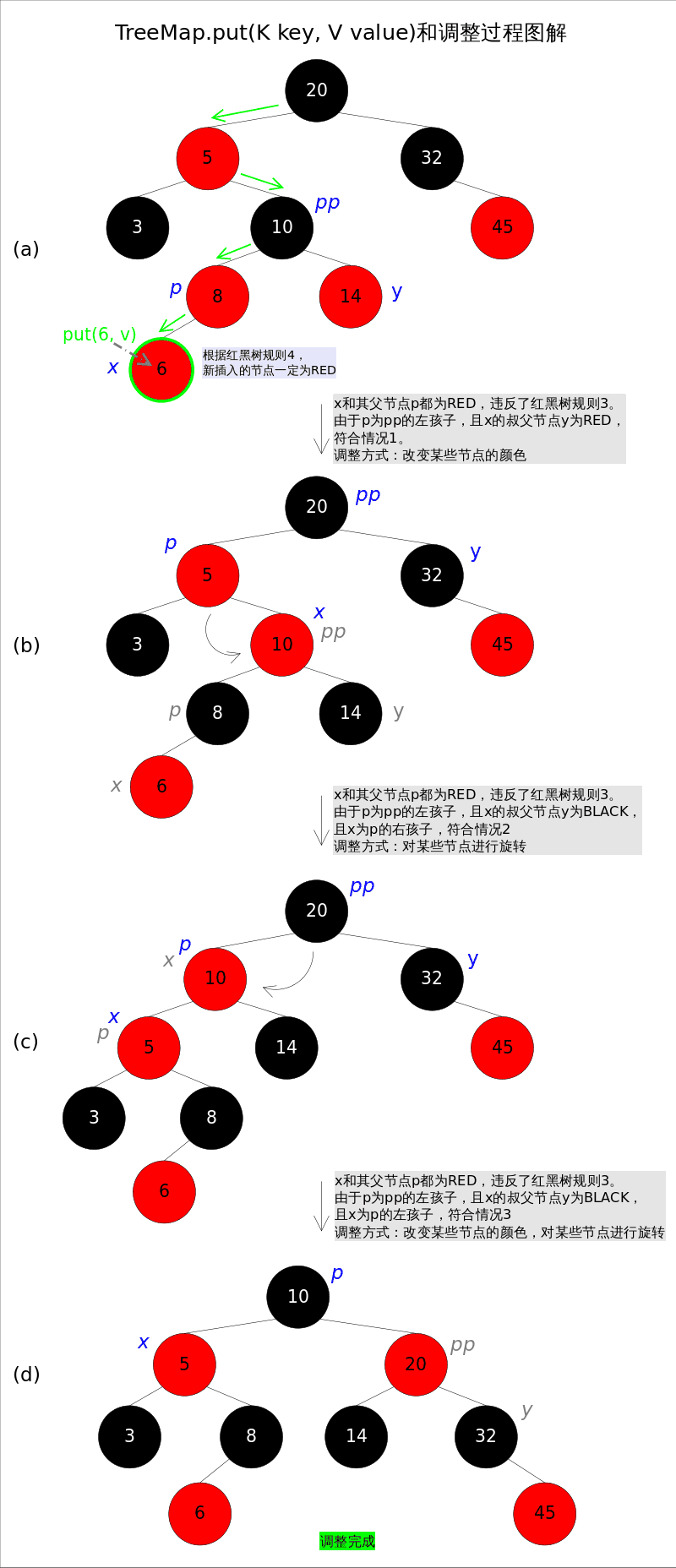
public V put(K key, V value) {
......
int cmp;
Entry<K,V> parent;
if (key == null)
throw new NullPointerException();
Comparable<? super K> k = (Comparable<? super K>) key;//使用元素的自然顺序
do {
parent = t;
cmp = k.compareTo(t.key);
if (cmp < 0) t = t.left;//向左找
else if (cmp > 0) t = t.right;//向右找
else return t.setValue(value);
} while (t != null);
Entry<K,V> e = new Entry<>(key, value, parent);//创建并插入新的entry
if (cmp < 0) parent.left = e;
else parent.right = e;
fixAfterInsertion(e);//调整
size++;
return null;
}上述代码的插入部分并不难理解: 首先在红黑树上找到合适的位置,然后创建新的entry并插入(当然,新插入的节点一定是树的叶子)。难点是调整函数fixAfterInsertion(),前面已经说过,调整往往需要1.改变某些节点的颜色,2.对某些节点进行旋转。
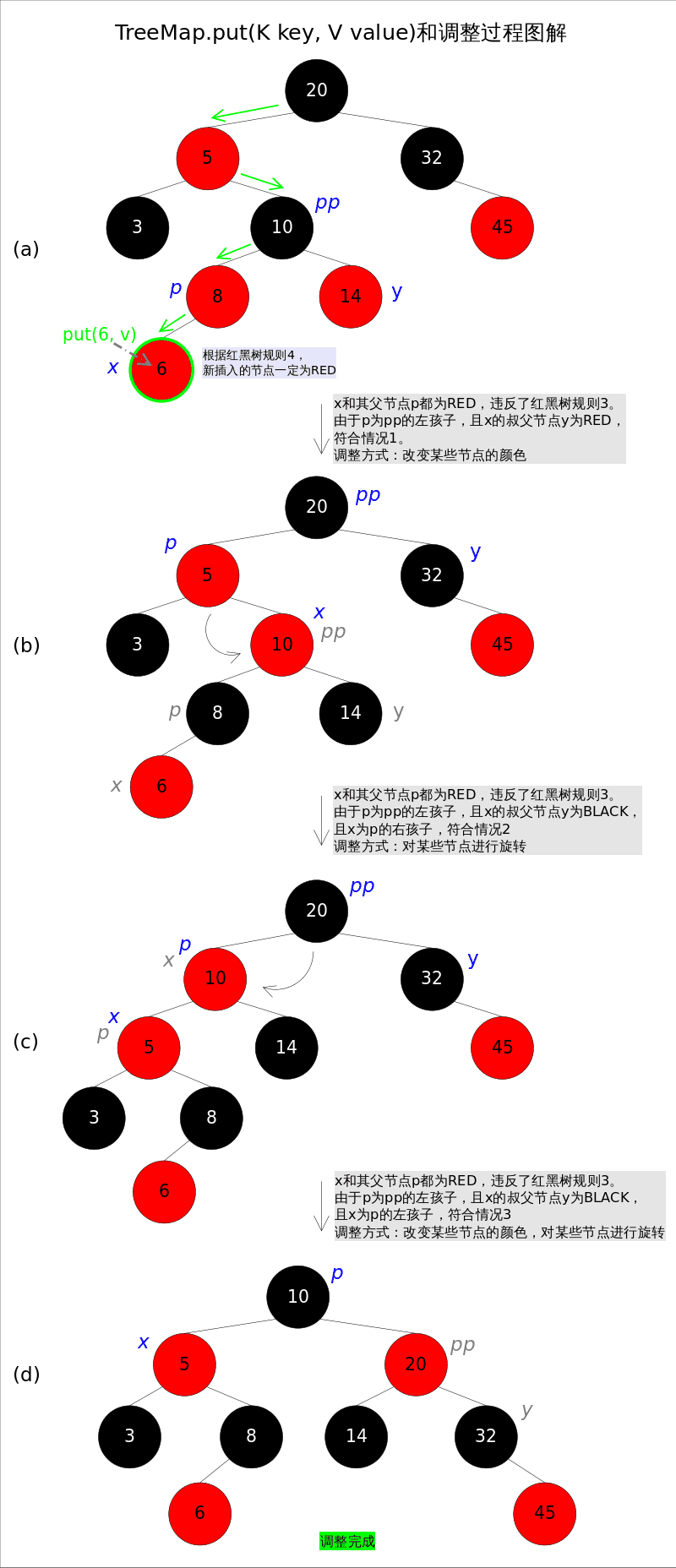
调整函数fixAfterInsertion()的具体代码如下,其中用到了上文中提到的rotateLeft()和rotateRight()函数。通过代码我们能够看到,情况2其实是落在情况3内的。情况4~情况6跟前三种情况是对称的,因此图解中并没有画出后三种情况,读者可以参考代码自行理解。
//红黑树调整函数fixAfterInsertion()
private void fixAfterInsertion(Entry<K,V> x) {
x.color = RED;
while (x != null && x != root && x.parent.color == RED) {
if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
Entry<K,V> y = rightOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK); // 情况1
setColor(y, BLACK); // 情况1
setColor(parentOf(parentOf(x)), RED); // 情况1
x = parentOf(parentOf(x)); // 情况1
} else {
if (x == rightOf(parentOf(x))) {
x = parentOf(x); // 情况2
rotateLeft(x); // 情况2
}
setColor(parentOf(x), BLACK); // 情况3
setColor(parentOf(parentOf(x)), RED); // 情况3
rotateRight(parentOf(parentOf(x))); // 情况3
}
} else {
Entry<K,V> y = leftOf(parentOf(parentOf(x)));
if (colorOf(y) == RED) {
setColor(parentOf(x), BLACK); // 情况4
setColor(y, BLACK); // 情况4
setColor(parentOf(parentOf(x)), RED); // 情况4
x = parentOf(parentOf(x)); // 情况4
} else {
if (x == leftOf(parentOf(x))) {
x = parentOf(x); // 情况5
rotateRight(x); // 情况5
}
setColor(parentOf(x), BLACK); // 情况6
setColor(parentOf(parentOf(x)), RED); // 情况6
rotateLeft(parentOf(parentOf(x))); // 情况6
}
}
}
root.color = BLACK;
}3、remove()
remove(Object key)的作用是删除key值对应的entry,该方法首先通过上文中提到的getEntry(Object key)方法找到key值对应的entry,然后调用deleteEntry(Entry<K,V> entry)删除对应的entry。由于删除操作会改变红黑树的结构,有可能破坏红黑树的约束条件,因此有可能要进行调整。
getEntry()函数前面已经讲解过,这里重点放deleteEntry()上,该函数删除指定的entry并在红黑树的约束被破坏时进行调用fixAfterDeletion(Entry<K,V> x)进行调整。
由于红黑树是一棵增强版的二叉查找树,红黑树的删除操作跟普通二叉查找树的删除操作也就非常相似,唯一的区别是红黑树在节点删除之后可能需要进行调整。现在考虑一棵普通二叉查找树的删除过程,可以简单分为两种情况:
删除点p的左右子树都为空,或者只有一棵子树非空。
删除点p的左右子树都非空。
对于上述情况1,处理起来比较简单,直接将p删除(左右子树都为空时),或者用非空子树替代p(只有一棵子树非空时);对于情况2,可以用p的后继s(树中大于x的最小的那个元素)代替p,然后使用情况1删除s(此时s一定满足情况1.可以画画看)。
基于以上逻辑,红黑树的节点删除函数deleteEntry()代码如下:
// 红黑树entry删除函数deleteEntry()
private void deleteEntry(Entry<K,V> p) {
modCount++;
size--;
if (p.left != null && p.right != null) {// 2. 删除点p的左右子树都非空。
Entry<K,V> s = successor(p);// 后继
p.key = s.key;
p.value = s.value;
p = s;
}
Entry<K,V> replacement = (p.left != null ? p.left : p.right);
if (replacement != null) {// 1. 删除点p只有一棵子树非空。
replacement.parent = p.parent;
if (p.parent == null)
root = replacement;
else if (p == p.parent.left)
p.parent.left = replacement;
else
p.parent.right = replacement;
p.left = p.right = p.parent = null;
if (p.color == BLACK)
fixAfterDeletion(replacement);// 调整
} else if (p.parent == null) {
root = null;
} else { // 1. 删除点p的左右子树都为空
if (p.color == BLACK)
fixAfterDeletion(p);// 调整
if (p.parent != null) {
if (p == p.parent.left)
p.parent.left = null;
else if (p == p.parent.right)
p.parent.right = null;
p.parent = null;
}
}
}上述代码中占据大量代码行的,是用来修改父子节点间引用关系的代码,其逻辑并不难理解。下面着重讲解删除后调整函数fixAfterDeletion()。首先请思考一下,删除了哪些点才会导致调整?只有删除点是BLACK的时候,才会触发调整函数,因为删除RED节点不会破坏红黑树的任何约束,而删除BLACK节点会破坏规则4。
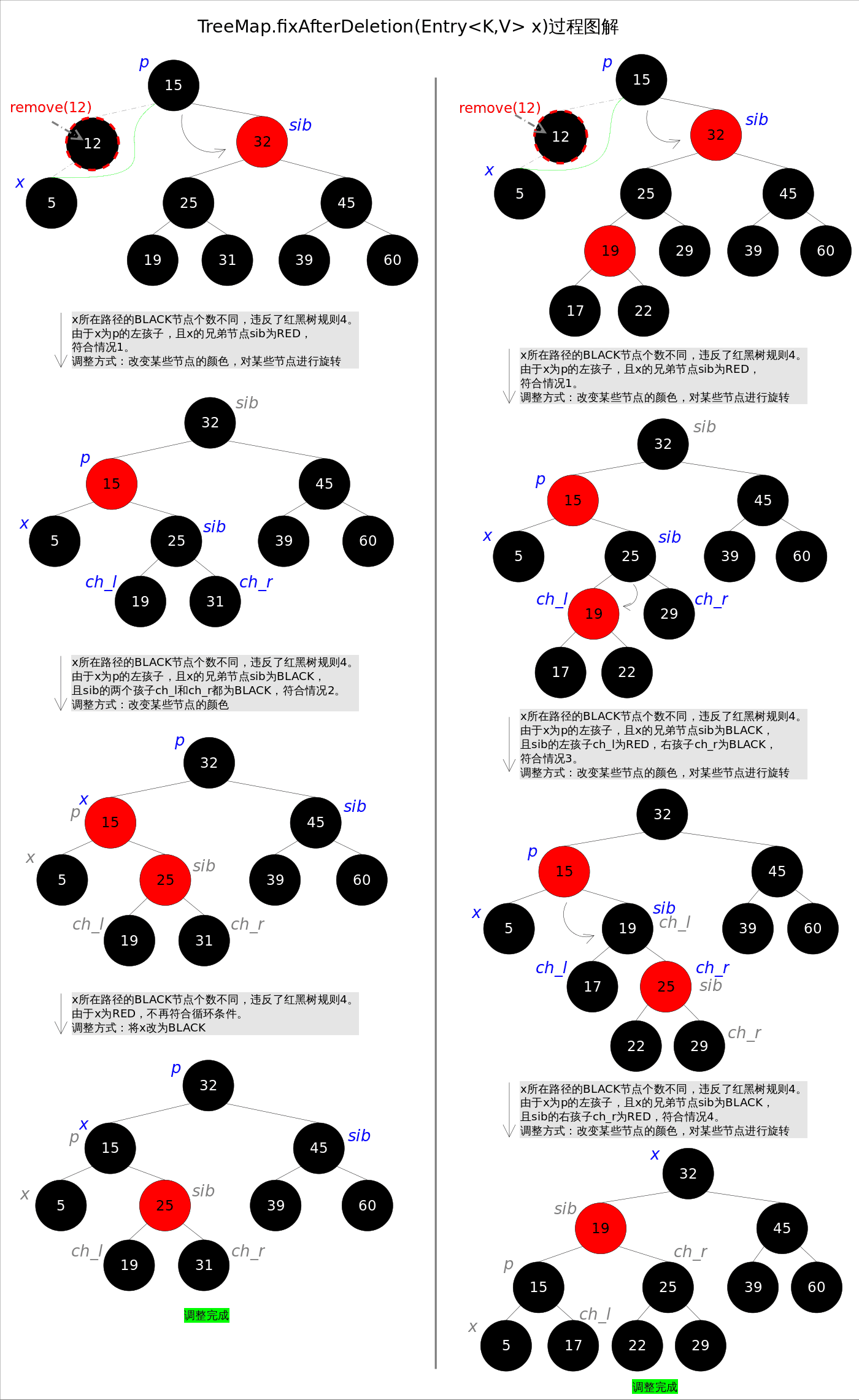
跟上文中讲过的fixAfterInsertion()函数一样,这里也要分成若干种情况。记住,无论有多少情况,具体的调整操作只有两种: 1.改变某些节点的颜色,2.对某些节点进行旋转。
上述图解的总体思想是: 将情况1首先转换成情况2,或者转换成情况3和情况4。当然,该图解并不意味着调整过程一定是从情况1开始。通过后续代码我们还会发现几个有趣的规则: a).如果是由情况1之后紧接着进入的情况2,那么情况2之后一定会退出循环(因为x为红色);b).一旦进入情况3和情况4,一定会退出循环(因为x为root)。
删除后调整函数fixAfterDeletion()的具体代码如下,其中用到了上文中提到的rotateLeft()和rotateRight()函数。通过代码我们能够看到,情况3其实是落在情况4内的。情况5~情况8跟前四种情况是对称的,因此图解中并没有画出后四种情况,读者可以参考代码自行理解。
private void fixAfterDeletion(Entry<K,V> x) {
while (x != root && colorOf(x) == BLACK) {
if (x == leftOf(parentOf(x))) {
Entry<K,V> sib = rightOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK); // 情况1
setColor(parentOf(x), RED); // 情况1
rotateLeft(parentOf(x)); // 情况1
sib = rightOf(parentOf(x)); // 情况1
}
if (colorOf(leftOf(sib)) == BLACK &&
colorOf(rightOf(sib)) == BLACK) {
setColor(sib, RED); // 情况2
x = parentOf(x); // 情况2
} else {
if (colorOf(rightOf(sib)) == BLACK) {
setColor(leftOf(sib), BLACK); // 情况3
setColor(sib, RED); // 情况3
rotateRight(sib); // 情况3
sib = rightOf(parentOf(x)); // 情况3
}
setColor(sib, colorOf(parentOf(x))); // 情况4
setColor(parentOf(x), BLACK); // 情况4
setColor(rightOf(sib), BLACK); // 情况4
rotateLeft(parentOf(x)); // 情况4
x = root; // 情况4
}
} else { // 跟前四种情况对称
Entry<K,V> sib = leftOf(parentOf(x));
if (colorOf(sib) == RED) {
setColor(sib, BLACK); // 情况5
setColor(parentOf(x), RED); // 情况5
rotateRight(parentOf(x)); // 情况5
sib = leftOf(parentOf(x)); // 情况5
}
if (colorOf(rightOf(sib)) == BLACK &&
colorOf(leftOf(sib)) == BLACK) {
setColor(sib, RED); // 情况6
x = parentOf(x); // 情况6
} else {
if (colorOf(leftOf(sib)) == BLACK) {
setColor(rightOf(sib), BLACK); // 情况7
setColor(sib, RED); // 情况7
rotateLeft(sib); // 情况7
sib = leftOf(parentOf(x)); // 情况7
}
setColor(sib, colorOf(parentOf(x))); // 情况8
setColor(parentOf(x), BLACK); // 情况8
setColor(leftOf(sib), BLACK); // 情况8
rotateRight(parentOf(x)); // 情况8
x = root; // 情况8
}
}
}
setColor(x, BLACK);
}五、TreeSet
前面已经说过TreeSet是对TreeMap的简单包装,对TreeSet的函数调用都会转换成合适的TreeMap方法,因此TreeSet的实现非常简单。这里不再赘述。
// TreeSet是对TreeMap的简单包装
public class TreeSet<E> extends AbstractSet<E>
implements NavigableSet<E>, Cloneable, java.io.Serializable
{
......
private transient NavigableMap<E,Object> m;
// Dummy value to associate with an Object in the backing Map
private static final Object PRESENT = new Object();
public TreeSet() {
this.m = new TreeMap<E,Object>();// TreeSet里面有一个TreeMap
}
......
public boolean add(E e) {
return m.put(e, PRESENT)==null;
}
......
}参考:
| Java 全栈知识体系