【原文链接】数据分析----IQR（Interquartile Range）四分位距的理解与应用及Python实现

一、IQR（Interquartile Range）四分位距的含义

1.1 IQR的官方定义

IQR 是用于标记离群值的另一种稳健方法。用于检测离群值的 IQR（Interquartile Range，四分位距）方法由 John Tukey 开发，他是开创探索性数据分析的先锋人物。此方法产生于手工计算和绘图时代，因此涉及的数据集通常较小，并且重点放在理解数据的意义上。

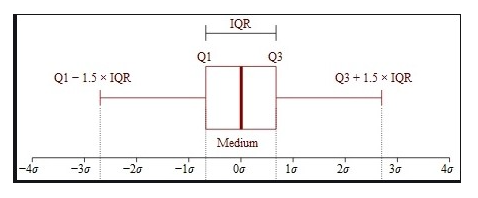
盒须图使用四分位数（将数据划分为大小相等的四组点）来绘制数据的形状。盒子代表第 1 个和第 3 个四分位数，它们等于第 25 个和第 75 个百分点。盒子内的线代表第二个四分位数，即中间值。

四分位距（该离群值检测方法正是因此而得名）是第一个和第三个四分位数（盒子边缘）之间的间距。Tukey 认为，如果数据点比第一个四分位数低 1.5 乘 IQR，或比第三个四分位数高 1.5 乘 IQR，就属于离群或极度离群。在经典的盒须图中，须线一直延伸到界限内的最后一个数据点。

四分位距 (IQR) 是一种衡量变异性的方法，它通过将数据集划分为四分位数来实现。四分位数将一个按等级排序的数据集划分为四个相等的部分。即 Q1（第 1 个四分位数）、Q2（第 2 个四分位数）和 Q3（第 3 个四分位数）。IQR 定义为 Q3–Q1，位于 Q3+1.5IQR 或 Q1-1.5IQR 之外的数据被视为离群值。

1.2 IQR的通俗理解

IQR的官方定义相对来说显得晦涩了一点，这里简单的解释一下，通俗一点来说就是对一个数据列表从小到大排序，然后分为四份，四分之一位置的点为Q1，四份之二位置的点为Q2，四份之三位置的点为Q3，这样中间的位置点就是Q2,Q3和Q1之间的差为△，也就是IQR的值，然后计算有效数据的上限和下限，上限为Q2+1.5△，下限为Q2-1.5△，在（Q2-1.5△，Q2+1.5△）之外的数据则视为离散数据，即无效数据，假如我们有更大规模的数据需要过滤，就可以使用（Q2-1.5△，Q2+1.5△）范围进行有效数据筛选。

Python代码实现

用python实现当然可以一个一个循环去计算，但是python的numpy库提供了非常好用的封装函数，这里就不再去一个一个计算了，而是直接使用numpy库进行处理了，实现代码如下

import numpy as np

def get_iqr_data(datas):
    q1=np.quantile(datas,0.25)
    q2=np.median(datas)
    q3=np.quantile(datas,0.75)
    iqr=q3-q1
    down=q2-1.5*iqr
    up=q2+1.5*iqr
    return [q1,q2,q3,iqr,down,up]

if __name__=="__main__":
    x=[1,2,3,4,5,6,7,8,9,10,11]
    rs=get_iqr_data(x)
    print(rs)

执行结果如下，当然在执行之前需要却把安装了numpy，如果还没有安装可以直接使用pip install numpy 即可安装

[3.5, 6.0, 8.5, 5.0, -1.5, 13.5]

通过这里的执行结果可以看住，在数据列表 [1,2,3,4,5,6,7,8,9,10,11] 中，四分之一的点的数据为3.5，这是因为总共11个数，四分之一落在了两个数之间，四分之二的点恰好就是第6个数了，四分之三的点又落在了两个数据之间，所以是8.5，那么这里IQR就是q3-q1即5.0，通过公式计算此时有效范围为(-1.5,13.5)，超出此范围的数据为无效数据