文章目录

动态规划
- 背包问题
- - 01背包
  - - 抽象出求解目标
    - 尝试进程子问题拆分
    - 基本情况
    - 根据拆分过程定义dp数组与转移方程
    - 遍历顺序与状态压缩
    - 模板归纳
    - 题目应用
    - 变种提升
    - - 组合问题
      - 多维01背包
      - 有特殊限制的01背包
  - 完全背包
  - - 尝试进行子问题拆分
    - 转移方程
    - 题目应用
    - 变种提升-求组合/排列数
- 打家劫舍
- - 变种提升
  - - 二分答案+打家劫舍
    - 树形打家劫舍
    - 图上打家劫舍
- 股票系列/状态机dp
- - 基础
  - 进阶
  - 闯关类题目
- 子序列类
- - 最长递增子序列/子数组
  - 最长公共子序列/数组
  - 公共子序列问题变种
  - 编辑距离
  - 最长回文子序列/子串
  - - 中心扩散算法
    - 动态规划解法

动态规划

背包问题

01背包

有C0-Cx件物品，每个物品价值对应为V0-Vx，有容量为N的背包，问背包能够装的最大价值。

由于每件物品只有装与不装两个状态，因此称为01背包。

抽象出求解目标

目标：C0-Cx可选，价值V0-Vx，容量为N能够装下的最大值。

尝试进程子问题拆分

子问题拆分：
假设：Cx物品选了，那么问题缩减为求解：
C0-Cx-1可选，价值V0 - Vx-1，容量为N-Vx，能够装下的最大值。
假设：Cx物品不选，那么问题缩减为求解：
C0-Cx-1可选，价值V0 - Vx-1，容量为N，能够装下的最大值。

基本情况

很显然，每件物品我们都可以按照上边的想法进行拆分求解。
当容量为0，价值为0。

根据拆分过程定义dp数组与转移方程

定义：dp[i][j]为物品0-i任意取，放进容量为j的背包中能够装的最大重量。

转移方程：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - value[i]]);

遍历顺序与状态压缩

dp[i][j]依赖它的上边和左上边的数据结果，因此，遍历顺序自上而下，自左而右。

滚动数组：由于每个数据只依赖上一行两个数据的结果，因此可以使用滚动数组来更新dp数组，由于需要的是左上方的数据和上方的数据，因此，对于背包容量我们逆序遍历时，遍历到某个位置时，此时的滚动数组就保留了左上和上的结果;
即dp[j] = max(d[j], dp[j - value[i]]);

模板归纳

枚举每个物品，逆序遍历背包，递推公式为dp[j] = max(d[j], dp[j - value[i]]);

题目应用

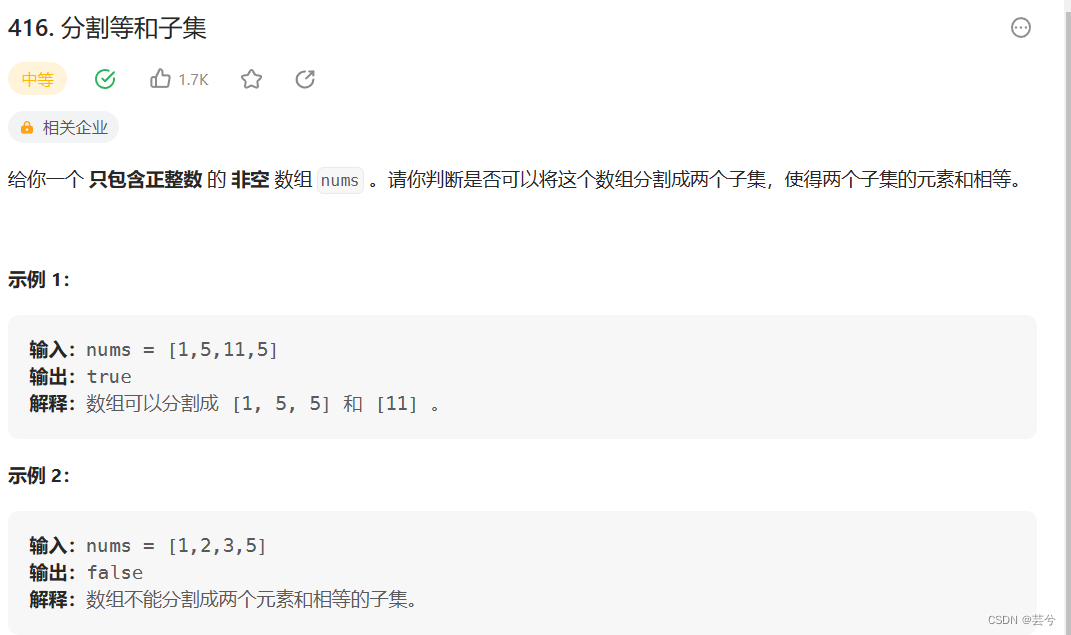
在这里插入图片描述
子集就是每个元素选或不选，最后构成的一种组合。计算数组的总和为sum，如果给定背包容量为sum / 2 能够装满，那么就存在，否则不存在。

 bool canPartition(vector<int>& nums) {
	int sum = accumulate(nums.begin(), nums.end(), 0);
	if (sum & 1) return false; // 如果sum为奇数，必不可等分
	int target = sum >> 1; // 最终要找的组合，它的累计和是nums累计和的一半。
    vector<int> dp(target + 1, 0);
	for (int num : nums) {
		for (int j = target; j >= num; --j) dp[j] = max(dp[j], dp[j - num] + num);
	}
	return dp[target] == target;
}

变种提升

组合问题

01背包还可以用于计算装满容量为N的物品的组合数。
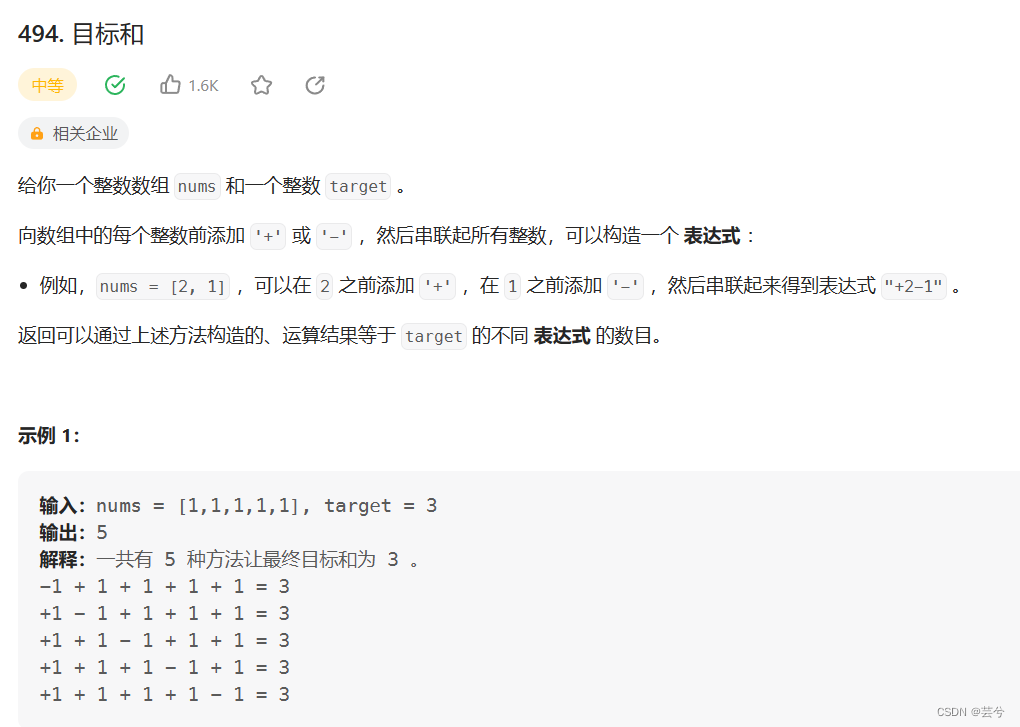
在这里插入图片描述
n个数，每个数可以是正负两种状态，不过这里要求的是组合数。

首先，由于符号未定，我们的物品是不确定的。
但是元素总和是确定的sum，
假设加法总和为x，所有元素总和为sum，那么减法元素总和为sum - x。
target = x - (sum - x) = 2x - sum
x = (sum + target) / 2

sum和target都是已知的。

因此也就是，问题可以转为装满容量为x的背包的方法数。
这样就只用考虑正数。

设dp[i][j]表示0-i元素任意选，装满j的方法数：
假设i选择：
dp[i][j] = dp[i - 1][j - nums[i]]
假设i不选：
dp[i][j] = dp[i - 1][j]

总方法数：
dp[i][j] = dp[i - 1][j - nums[i]] + dp[i - 1][j]

状态转移方程与01背包几乎一致，考虑滚动数组压缩：
dp[j] = dp[j - nums[i]] + dp[j]
进一步：
dp[j] += dp[j - nums[i]]

此外注意：求方法数时，容量为0，方法数为1，即都不选!!!。

    int findTargetSumWays(vector<int>& nums, int target) {
		int sum = accumulate(nums.begin(), nums.end(), 0);
		if (abs(target) > sum) return 0;
		if ((target + sum) % 2) return 0;
		int bagSize = (target + sum) >> 1;
		vector<int> dp(bagSize + 1);
		dp[0] = 1;
		for (int num : nums) {
			for (int j = bagSize; j >= num; --j) {
				dp[j] += dp[j - num];
			}
		} 
    }
    return dp[bagSize];

多维01背包

在这里插入图片描述
同样是子集问题，每个元素选或者不选两种情况，所不同的时，有0和1两方面的限制，即背包容量的维度是2维的。

dp[i][j][k]表示0-i物品任意选，0的容量为j，1的容量为k，能够装的物品数。
子情况拆分：
第i个选品如果选：假设第i个物品0的个数为cnt0i、1的个数为cnt1i。
dp[i][j][k] = dp[i - 1][j - cnt0i][cnt1i] + 1;
第i个物品如果不选：
dp[i][j][k] = dp[i][j][k];

转移方程和01背包一致，只依赖上方和左上方，可以逆序遍历背包容量来做成滚动数组形式;

int findMaxForm(vector<string>& strs, int m, int n) {
    vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));
    for (const string &str : strs) {
        int cntOne = 0;
        for (char c : str) cntOne += c - '0';
        int cntZero = str.size() - cntOne;
        for (int i = m; i >= cntZero; --i) {
            for (int j = n; j >= cntOne; --j) {
                dp[i][j] = max(dp[i][j], dp[i - cntZero][j - cntOne] + 1);
            }
        }
    }
    return dp[m][n];
}

有特殊限制的01背包

在这里插入图片描述

这道题也是0、1背包，但是物品有主件和附件之分，每个主件可以有0,1或者2个附件，附件必须依赖主件。

有主附之分的物品是无法直接应用01背包模板的，我们需要把元素进行组装。

具体而言，一个元素的价格有四种可能，主件，主件+附件1，主件+附件2，主件+附件1+附件2。

相应的，也需要把物品的价值（即满意度进行组装）

注意点：
1、从示例2可以看出，行号为物品编号，附件可以出现在主件前，因此先用prices和values先把数据保存下来。
2、主件价格为0可以直接跳过
3、遍历每个主件时，将它与附件进行组合：主件，主件+附件1，主件+附件2，主件+附件1+附件2。
4、应用背包模板，逆序遍历背包容量。
5、输入都除10，可以降低时空复杂度，但需要注意后边输出时乘回来。

#include <bits/stdc++.h>
#include <vector>
using namespace std;

int main() {
    int N, m;
    cin >> N >> m;
    N /= 10;
    vector<vector<int>> prices(m + 1, vector<int> (4)), values (m + 1, vector<int> (4));
    // prices[i]：3个元素，分别为i号主件价格，i号主件的附件1价格，i号主件的附件2价格
    for (int i = 1; i <= m; ++i) {
        int v, p, q;
        cin >> v >> p >> q;
        v /= 10;
        p *= v;
        if (q == 0) {
            // 0 : 主件
            prices[i][0] = v;
            values[i][0] = p;
        } else {
            if (prices[q][1] == 0) {
                // 1 : 附件1
                prices[q][1] = v;
                values[q][1] = p;
            } else {
                // 2 : 附件2
                prices[q][2] = v;
                values[q][2] = p;
            }
        }
    }
    vector<int> dp(N + 1);
    for (int i = 1; i <= m; ++i) {
        if (prices[i][0] == 0) continue;
        int p1 = prices[i][0], p2 = p1 + prices[i][1], p3 = p1 + prices[i][2], p4 = p2 + p3 - p1;
        int v1 = values[i][0], v2 = v1 + values[i][1], v3 = v1 + values[i][2], v4 = v2 + v3 - v1; 
        for (int j = N; j >= p1; --j) {
            dp[j] = j >= p1 ? max(dp[j], dp[j - p1] + v1) : dp[j];
            dp[j] = j >= p2 ? max(dp[j], dp[j - p2] + v2) : dp[j];
            dp[j] = j >= p3 ? max(dp[j], dp[j - p3] + v3) : dp[j];
            dp[j] = j >= p4 ? max(dp[j], dp[j - p4] + v4) : dp[j];
        }
    }
    cout << dp[N] * 10 << endl;
    return 0;
}

完全背包

有C0-Cx种物品，每种物品价值对应为V0-Vx，每中物品的供应不限，有容量为N的背包，问背包能够装的最大价值。

完全背包与01背包的最大区别在于每种物品，01背包只有取与不取两种状态，而完全背包是不限制取的次数

仍然可以用dp[i][j]来表示0-i种物品任意选，背包容量为j，能够获取的最多的价值。

尝试进行子问题拆分

第i种物品：
不选， dp[i][j] = dp[i - 1][j]
选1件，dp[i][j] = dp[i - 1][j - wi] + vi
选2件，dp[i][j] = dp[i - 1][j - 2 ×wi] + 2×vi
……
选x件 dp[i][j] = dp[i - 1][j - x ×wi] + x×vi

因为背包容量是有限的，所以细分的种类是有限的，如果是01背包是二叉树枚举，那么完全背包就是多叉树枚举。
取上边所有情况的最大值的结果。

转移方程

01背包中我们为了使用滚动数组求解，逆序遍历背包容量，以保证求解d[j]时，dp[j - wi]是上一层的结果。

完全背包中，我们顺序遍历背包容量，对于每个物品即可实现多次取，例如，假设第一个物品，占空间为1，价值为2.
dp[1] = max(dp[1], dp[1 - 1] + 2) = 2;
dp[2] = max(dp[2], dp[2 - 1] + 2) = 4;
可以看到的dp[2]的时候是放入了两次物品1。

题目应用

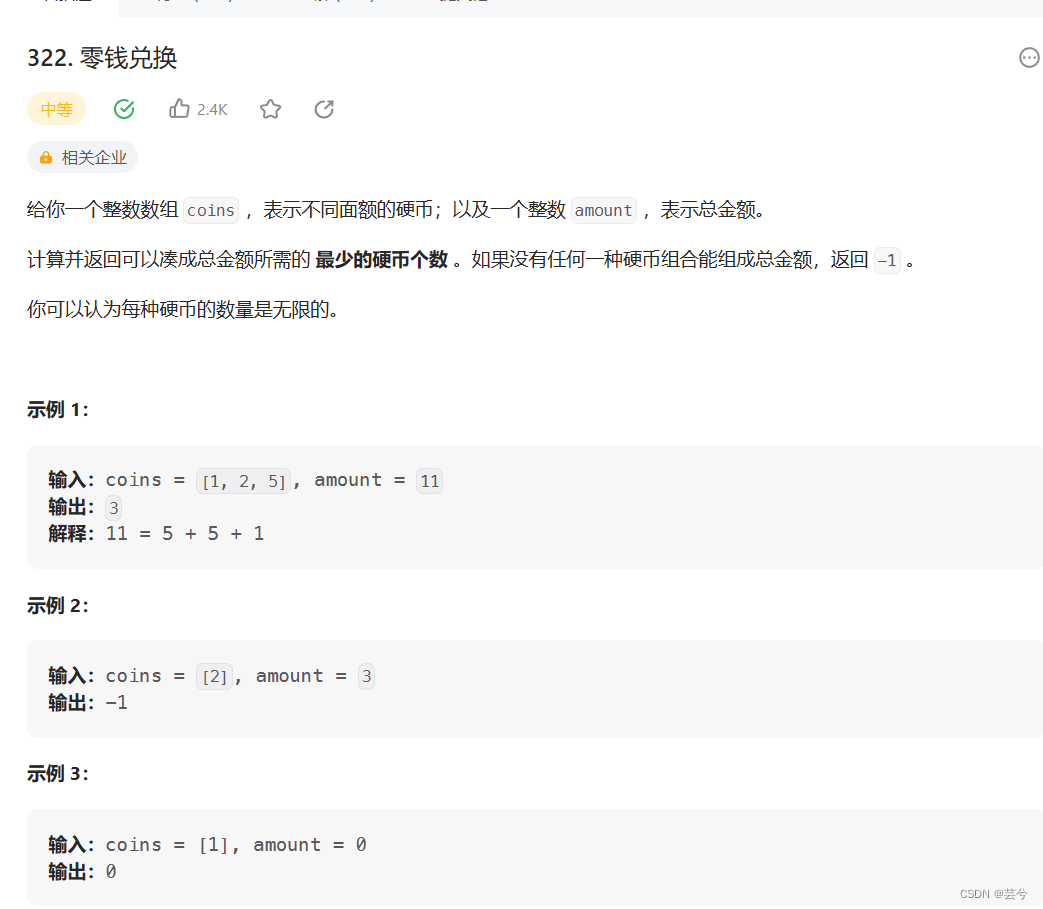
在这里插入图片描述
每个硬币无限，求构成指定目标需要的最少硬币数。

    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount + 1, INT_MAX); // 
        dp[0] = 0;
        for (int c : coins) {
            for (int j = c; j <= amount; ++j) {
                if (dp[j - c] != INT_MAX) {
                    dp[j] = min(dp[j], dp[j - c] + 1);
                }
            }
        }
        return dp[amount] == INT_MAX ? -1 : dp[amount];
    }

变种提升-求组合/排列数

1、使用完全背包的思路求解组合排列问题，先遍历物品后遍历背包容量得到组合数，先遍历背包容量后遍历物品，得到排列数

2、应注意遍历的起始点，内层遍历背包容量时，从coins[i]开始遍历，因为小于coins[i]的容量放不下，沿用之前的结果。内层遍历物品时，遍历范围是所有物品，但要注意，仅在j - coins[i] >= 0，即当前的容量可以放下该物品时，进行状态转移。

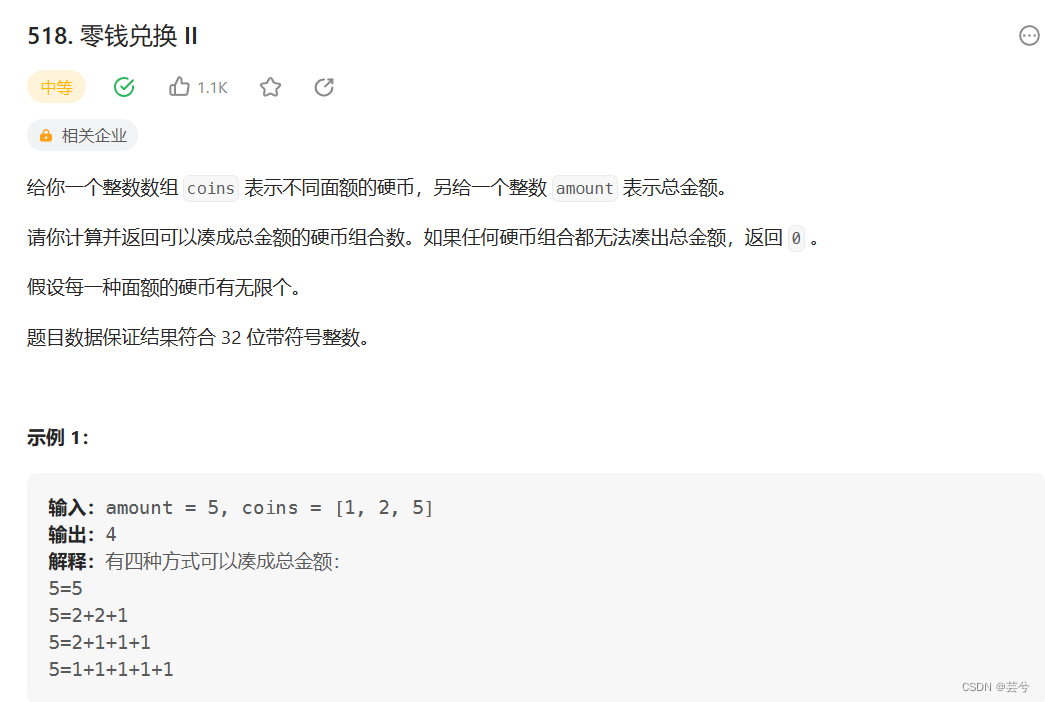
在这里插入图片描述

    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount + 1, 0);
        dp[0] = 1;
        for (int c : coins) {
            for (int j = c; j <= amount; ++j) {
                dp[j] += dp[j - c];
            }
        }
        return dp[amount];
    }

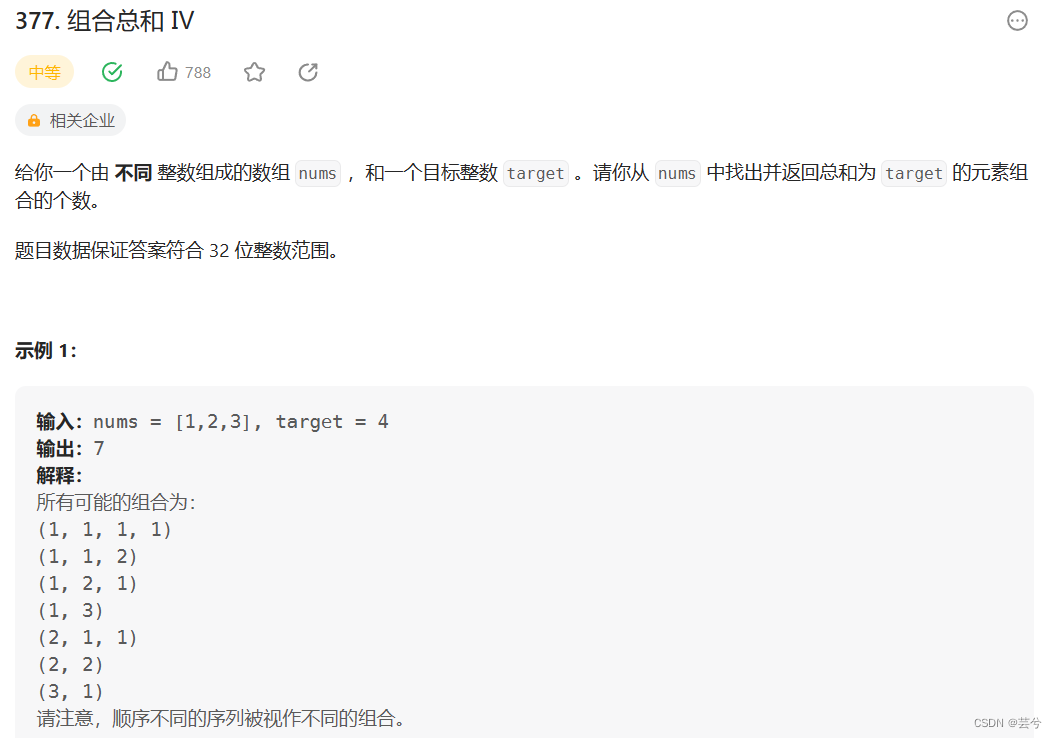
在这里插入图片描述

    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target + 1);
        dp[0] = 1;
        for (int j = 0; j <= target; ++j) {
            for (int n : nums) {
                if (j - n >= 0 &&  dp[j] <= INT_MAX - dp[j - n]) dp[j] += dp[j - n];
            }
        }
        return dp[target];
    }

注意：题目保证答案结果符合32位整数范围，但是我们dp表中的结果有可能不符合，会越界，但既然答案不越界，那么dp表中就没有必要记录越界的状态更新。

因此加上dp[j] <= INT_MAX - dp[j - n]只在不越界时，更新状态。

打家劫舍

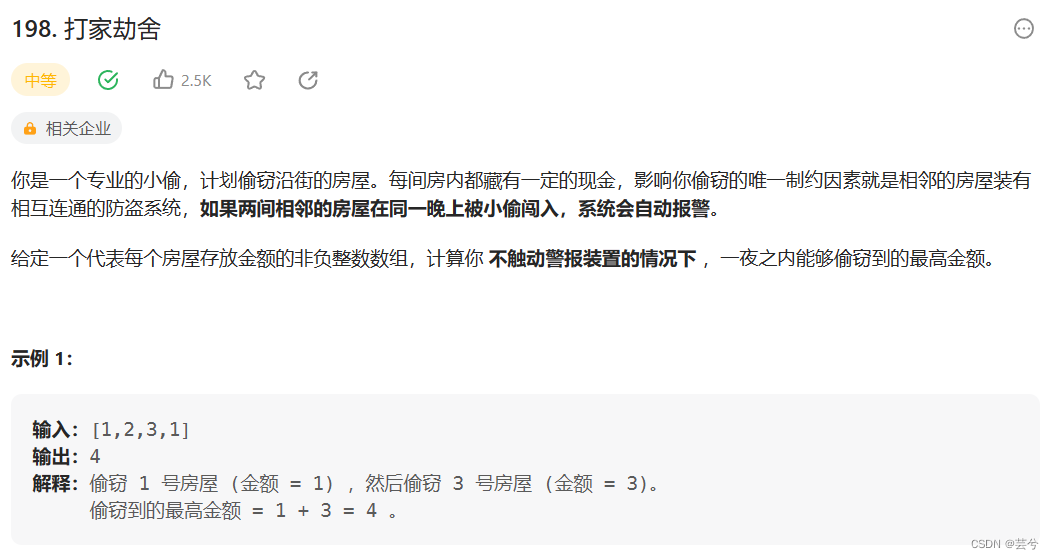
在这里插入图片描述
问题抽象：0-i个元素任意偷，不能偷相邻的，最多偷多少?
解：设最多偷dp[i]
假设第i个元素偷了，那么i-1必须不能偷，
问题缩减为：
dp[i] = vi + dp[i - 2]

假设第i个元素不偷，那么0-i-1任意偷
dp[i] = dp[i - 1];

综上 dp[i] = max(dp[i - 2] + vi, dp[i - i]);

由于仅依赖前面两个状态值，因此可以进行状态记录并转移：
初始状态都是0

    int rob(vector<int>& nums) {
        int pre1 = 0, pre2 = 0, cur = 0; // 前一个状态，前二个状态，当前状态
        for (int & n : nums) {
            cur = max(pre1, pre2 + n);
            pre2 = pre1;
            pre1 = cur;
        }
        return cur;
    }

变种提升

二分答案+打家劫舍

在这里插入图片描述
窃取能力c是从单间房屋中窃取的最大金额，显然如果窃取能力越大，能够窃取的房屋越多，具有单调性，最小化最大值，二分答案类型题目。

能够窃取的房屋数是打家劫舍的模板。

    int minCapability(vector<int> &nums, int k) {
        int left = 0, right = *max_element(nums.begin(), nums.end());  // 窃取能力的范围为0-单间最大值
        while (left + 1 < right) {
            int mid = left + (right - left) / 2;  // 猜中间数
            int f0 = 0, f1 = 0;
            for (int x : nums)  // 使用打家劫舍模板，查看在窃取能力为mid的情况下，能够窃取的最大房屋数f1
                if (x > mid) f0 = f1; // 如果x>mid，那么一定不能偷，直接=前一个状态
                else {
                    int tmp = f1;
                    f1 = max(f1, f0 + 1); // 前2个状态 + 1（偷）与（前一个状态不偷）
                    f0 = tmp;
                }
            (f1 >= k ? right : left) = mid; // 如果满足当前偷的房子数大于k，右移答案，否则左移答案
        }
        return right;
    }

树形打家劫舍

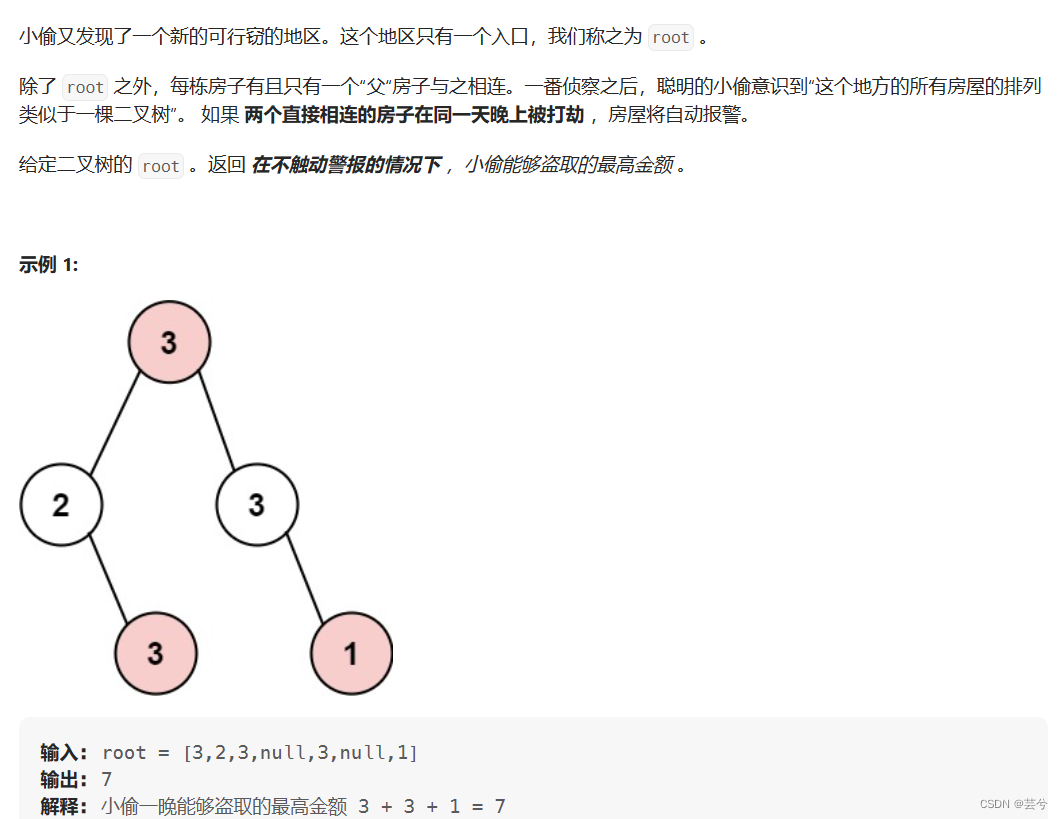
在这里插入图片描述
对于某个节点nodex：
如果选择偷，那么结果为valuex + 偷它的孩子节点的孩子节点。
如果选择不偷，那么结果为偷它的两个孩子节点。

    int rob(TreeNode* root) {
        if (!root) return 0;
        if (!root->left && !root->right) return root->val;
        int notcur = rob(root->left) + rob(root->right);
        int left = root->left ? rob(root->left->left) + rob(root->left->right) : 0;
        int right = root->right ? rob(root->right->right) + rob(root->right->left) : 0;
        int cur = root->val + left + right;
        return max(notcur, cur);
    }

以上代码超时了,我们计算了root的四个孙子（左右孩子的孩子）为头结点的子树的情况，又计算了root的左右孩子为头结点的子树的情况，计算左右孩子的时候其实又把孙子计算了一遍。

使用动态规划的思路是，我们将每个节点选或者不选的结果都返回。
如图该节点选：那么结果为valuei + 左右孩子不选的结果
如果该节点不选：那么结果为左右孩子选或者不选的最大结果之和。

    int rob(TreeNode* root) {
        pair<int, int> ans = robTree(root);
        return max(ans.first, ans.second);
    }

    pair<int, int> robTree(TreeNode* root) {
        if (!root) return {0, 0};
        pair<int, int> left = robTree(root->left);
        pair<int, int> right = robTree(root->right);
        int val0 = max(left.first, left.second) + max(right.first, right.second);
        int val1 = root->val + left.first + right.first;
        return {val0, val1};
    }

图上打家劫舍

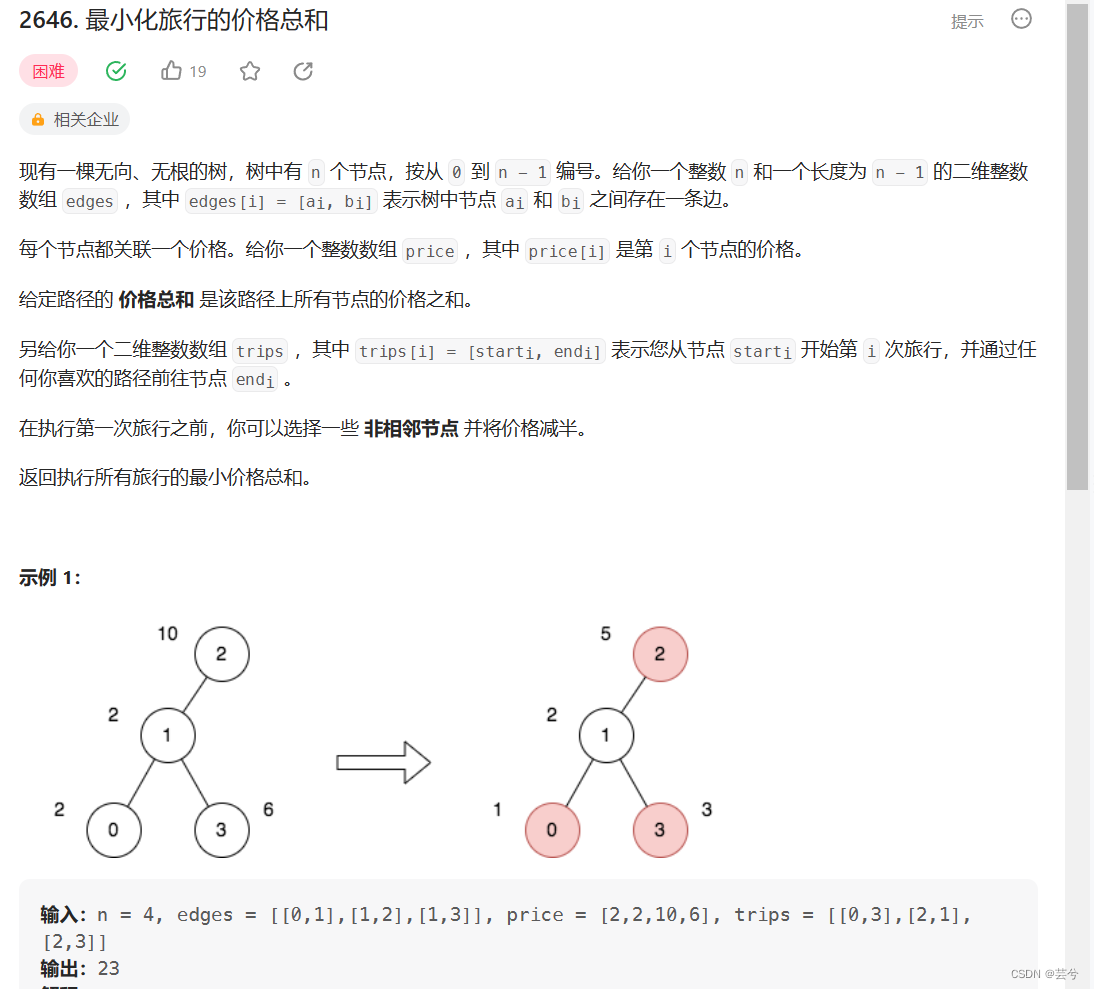
在这里插入图片描述
选择非相邻节点将价格减半的操作就类似于打家劫舍模板，非相邻节点偷或者不偷。

但是这道题要求返回旅行中的价格总和，因此我们需要将旅行中每个节点的经过次数统计处理，次数×每个节点的价格，才是每个节点在旅行中完整的花费。

统计出次数后，就可以应用打家劫舍模板解题。

    int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {
        vector<vector<int>> g(n);
        for (auto e : edges) {
            g[e[0]].push_back(e[1]);
            g[e[1]].push_back(e[0]);
        }
        vector<int> cnt(n);
        
        // 遍历trips，找到每一条路径，统计路径上的节点经过次数
        for (auto &t : trips) {
            int end = t[1];
            // 该节点是否为能到达终点的路径上的点
            function<bool(int, int)> dfs = [&](int x, int fa) ->bool {
               if (x == end) {
                   ++cnt[x];
                   return true;
               }
                for (int y : g[x]) {
                    if (y != fa && dfs(y, x)) {  // 当前节点的子节点为终点，也直接返回true
                        ++cnt[x];
                        return true;
                    }
                }
                return false;
            };
            dfs(t[0], -1);
        }

        // 打家劫舍模板
        function<pair<int, int>(int, int)> dfs = [&](int x, int fa) ->pair<int, int> {
            int not_halve = price[x] * cnt[x];
            int halve = not_halve / 2;
            for (int y : g[x]) {
                if (y != fa) {
                    auto [nh, h] = dfs(y, x);  // 获取每个子节点半价和非半价的价格总和
                    not_halve += min(nh, h);  // 如果当前非半价，子节点无限制，选择最小，因此加上min(nh, h)
                    halve += nh; // 如果当前半价了，那么只能取子节点非半价的结果
                }
            }
            return {not_halve, halve};
        };
        auto [nh, h] = dfs(0, -1);
        return min(nh, h);
    }

股票系列/状态机dp

股票系列的解法称为状态机dp，每一天的结果，依赖于前一天不同状态的结果。

状态机类问题，关键在于状态的定义与转换。

状态定义紧扣要求解的问题，比如股票系列，求利润，利润产生于每次交易，任何时候最多持有一股股票，那么定义持有和非持有两个状态，即可实现模拟这个交易的过程。

基础

在这里插入图片描述
每一天，我们可以选择买，也可以选择不买，但由于任何时候，我们最多只能持有一股股票，那么更为简单的状态定义为：当前持有股票，当前不持有股票。
状态定义：

尝试子问题拆分：
如果第i 天持有股票，那么第i天最大利润为前一天不持有股票，今天买入，或者前一天持有了股票，今天不动，选择最大，即：
dp[i][1] = max(dp[i - 1][0] - price[i]，dp[i - 1][1])
如果第i天不持有股票，那么第i天最大利润为前一天持有股票，今天卖出，或者前一天不持有股票，今天不动，取两者最大，即：
dp[i][0] = max(dp[i - 1][1] + price[i]，dp[i - 1][0])

    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2, 0)); // 每个点两个状态：持有股票和不持有股票
        dp[0][0] = 0;
        dp[0][1] = -prices[0];
        for (int i = 1; i < n; ++i) {
            dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        }
        return dp[n - 1][0];
    }

进阶

在这里插入图片描述
这里多出了交易次数的限制，可以新开一个维度，记录当前还有几次交易机会，当然也可以直接分类：
想象完成2次交易所经历的阶段：
初始 -> 第一次买入 -> 第一次卖出 -> 第二次买入 ->第二次卖出
为了便于判断，根据是否持有股票分为下边四个状态：
第一次持有，第一次不持有，第二次持有，第二次不持有

    int maxProfit(vector<int>& prices) {
        vector<vector<int>> dp(prices.size(), vector<int>(4, 0));
        dp[0][0] = -prices[0];
        dp[0][2] = -prices[0];
        for (int i = 1; i < prices.size(); ++i) {
            dp[i][0] = max(dp[i - 1][0], -prices[i]);
            dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]); 
            dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] - prices[i]);
            dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] + prices[i]);
        }
        return dp[prices.size() - 1][3];
    }

上边，两次交易的很容易发现规律，这次持有依赖于前一天的同等状态和非持有买入。

延展到k次交易：
在这里插入图片描述

    int maxProfit(int k, vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> dp(n, vector<int>(2 * k, 0)); // 偶数持有，奇数不持有
        for (int i = 0; i < 2 * k; i += 2) dp[0][i] = -prices[0]; // 持有的状态都初始化为买入
        for (int i = 1; i < n; ++i) {
            for (int j = 0; j < 2 * k; ++j) {
                if (j == 0) dp[i][j] = max(dp[i - 1][j], -prices[i]); // 第0次前面没有状态，单独处理
                else if (j & 1) dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] + prices[i]); // 奇数是不持有，前一次不持有保持，或者前一次持有，这次卖出  
                else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - 1] - prices[i]); // 偶数是持有，前一次持有保持，或者前一次不持有，这次买入  
            }
        }
        return dp[n - 1][2 * k - 1];

闯关类题目

闯关类题目，后边的关卡依赖前面关卡的处理结果，也是典型的状态机dp。
在这里插入图片描述
最终需要求赚的钱数，而只有在商人关卡可选则买出或者保留。
那么在商人关卡，首先如果我们没有商人需要的宝石，那么直接不能处理，沿用前一个关卡的状态。
如果有商人需要的宝石，可以选择买或者不卖，不卖依旧是沿用上一个状态，卖的话，说明这个类型的宝石从获取的关卡到当前的关卡，一直是持有

在每个boss关卡，我们记录宝石种类对应的关卡号。

#include <bits/stdc++.h>
#include <unordered_map>
using namespace std;

int main()
{
    int n, m;
    cin >> n >> m;
    vector<int> dp(n + 1, 0);
    unordered_map<int, int> collections;
    for (int i = 1; i <= n; ++i)
    {
        char boss;
        int type;
        int value;
        cin >> boss >> type >> value;
        if (boss == 'b')
        {
            collections[type] = i;
            dp[i] = dp[i - 1];
        }
        else
        {
            if (!collections.count(type))
            {
                dp[i] = dp[i - 1];
            }
            else
            {
                dp[i] = max(dp[i - 1], dp[collections[type]] + value);
            }
        }
    }

    cout << dp[n];
    return 0;
}

子序列类

子序列类题目，一般dp[i]的定义都是以i结尾的子序列或者前i个数，或者反向定义，以后缀的形式。

最长递增子序列/子数组

在这里插入图片描述
定义dp[i]为以下标i结尾的最长递增子序列的长度，
遍历i前边的元素，如果小于i位置，那么可以作为子序列的一部分，dp[i] = dp[j] + 1;
否则不行。

    int lengthOfLIS(vector<int>& nums) {
        // dp数组的含义：i之前的（包括i）以nums[i]结尾的最长子序列长度
        vector<int> dp(nums.size(), 1);
        int ans = 1;
        for (int i = 1; i < nums.size(); ++i) {
            for(int j = 0; j < i; ++j) {
                if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
            }
            ans = max(dp[i], ans);
        }
        return ans;
    }

在这里插入图片描述
如果要求连续，即求最长递增子串，那么对于每一个i，我们只需要它前一个数，与i位置相比，如果递增，在前一个位置上加一，否则以i位置结尾的最长子串为1.进一步可以状态压缩，因为只需要前一个状态。

    int findLengthOfLCIS(vector<int>& nums) {
        int ans = 1, pre = 1, cur = 1;
        for (int i = 1; i < nums.size(); ++i) {
            if (nums[i] > nums[i - 1]) cur = pre + 1;
            else cur = 1;
            pre = cur;
            ans = max(ans, cur);
        }
        return ans;

最长公共子序列/数组

在这里插入图片描述
定义dp[i][j]为num1[i]和nums[j]结尾的两子数组的最长公共子数组。

如果nums1[i] == nums2[j]，那么在d[i - 1][j - 1]的基础上加1，否则直接为0.
用ans记录遍历过程中的最大值。

    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        vector<vector<int>> dp(m + 1, vector<int> (n + 1));
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (nums1[i] == nums2[j]) dp[i + 1][j + 1] = dp[i][j] + 1;
                else dp[i + 1][j + 1] = 0;
                ans = max(ans, dp[i + 1][j + 1]);
            }
        }
        return ans;
    }

由于每个状态仅仅依赖它左上角的值，所有可以状态压缩，类似01背包，正序遍历nums1，逆序遍历nums2，即可使用滚动数组。

    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        vector<int> dp(n + 1);
        int ans = 0;
        for (int i = 0; i < m; ++i) {
            for (int j = n - 1; j >= 0; --j) {
                if (nums1[i] == nums2[j]) dp[j + 1] = dp[j] + 1;
                else dp[j + 1] = 0;
                ans = max(ans, dp[j + 1]);
            }
        }
        return ans;
    }

在这里插入图片描述

    int longestCommonSubsequence(string text1, string text2) {
        int m = text1.size(), n = text2.size();
        vector<vector<int>> dp(m + 1, vector<int> (n + 1));
        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                if (text1[i] == text2[j]) dp[i + 1][j + 1] = dp[i][j] + 1;
                else dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1]);
            }
        }
        return dp[m][n];
    }

公共子序列问题变种

不相交的线，要求数字相等才能连线，线之间不能相加，即公共连线只能向后延长。本质就是公共子序列！

在这里插入图片描述
两个字符串删除，使得相等，返回最小步数。

相同的子序列不必删除。那么求公共子序列长度，用两字符长度减去公共长度的2倍，即是不同的字符数。

在这里插入图片描述

编辑距离

在这里插入图片描述
删除一个字符和添加一个字符的操作本质是一样的。

如果两个位置字符相等，那么状态等于两个位置都前移一个；
如果不等：
可以：1、删除/插入 dp[i - 1][j] + 1 （删除str1的i位置）, dp[i][j -1 ] + 1（删除str2的j位置）
2、替换 dp[i][j] = dp[i - 1][j - 1] + 1
如果是题目，

    int minDistance(string word1, string word2) {
        vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
        for (int i = 0; i <= word1.size(); ++i) dp[i][0] = i;
        for (int j = 0; j <= word2.size(); ++j) dp[0][j] = j;
        for (int i = 1; i <= word1.size(); ++i) {
            for (int j = 1; j <= word2.size(); ++j) {
                if (word1[i - 1] == word2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
                else dp[i][j] = min(dp[i - 1][j - 1] + 1, min(dp[i - 1][j] + 1, dp[i][j - 1] + 1));
            }
        }
        return dp[word1.size()][word2.size()];
    }

最长回文子序列/子串

在这里插入图片描述

中心扩散算法

以某一个点作为中心，向左右扩散，直至不满足回文。
最终答案可能是奇回文，也可能是偶数回文。
所以，在扩散的时候，选择两个中心，如果是奇数，把两个中心设置为一样即可。
中心扩散：

string longestPalindrome(string s) {
    function<pair<int, int>(int, int)> centerExpand = [&](int i, int j) -> pair<int, int> {
        while (i >= 0 && j < s.size() && s[i] == s[j]) {--i; ++j;}
        return {i + 1, j - 1};
    };
    int left = 0, right = 0;
    for (int i = 0; i < s.size(); ++i) {
        auto [l1, r1] = centerExpand(i, i);
        auto [l2, r2] = centerExpand(i, i + 1);
        if (r1 - l1 > right - left) {right = r1; left = l1;}
        if (r2 - l2 > right - left) {right = r2; left = l2;}
    }
    return s.substr(left, right - left + 1);
}

动态规划解法

如果是找回文子序列，那么每次扩散时，遇到不相等的不可以直接结束，中心扩散的方法就不适用了。
在这里插入图片描述
假定dp[left,right]表示字符串s，从left到right之间的序列中，最长回文子序列的长度，那么如果s[left - 1] == s[right + 1],
就有dp[left - 1][right + 1] = dp[left][right] + 2;
或者说：dp[left][right] = dp[left + 1][right - 1] + 2;
如果不相等，沿用dp[left][right]的结果；

状态传递时注意：首先left 需要小于等于right
其次dp[left][right] = dp[left + 1][right - 1] + 2;
即依赖于它左下角的结果。

那么遍历的时候应该自下向上，自左向右；

int longestPalindromeSubseq(string s) {
    vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
    for (int i = 0; i < s.size(); ++i) dp[i][i] = 1;
    for (int i = s.size() - 1; i >= 0; --i) {
        for (int j = i + 1; j < s.size(); ++j) {
            if (s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
            else dp[i][j] = max(dp[i][j - 1], dp[i + 1][j]);
        }
    }
    return dp[0][s.size() - 1];
}