LightGBM^v^

LightGBM

LightGBM（Light Gradient Boosting Machine）是一个基于梯度提升决策树（GBDT）的高效机器学习框架。它是由微软公司开发的，旨在提供更快、更高效的训练和预测性能。LightGBM在许多数据科学竞赛中都表现出色，并被广泛应用于各种实际问题中，如推荐系统、搜索排名等。

LightGBM的主要特点：

更快的训练速度：相比于其他梯度提升树算法，如XGBoost，LightGBM在大数据集上能够更快地训练模型。

更低的内存占用：LightGBM使用了一种名为“基于直方图”的方法，将连续特征分桶，从而减少内存使用。

更好的准确性：通过使用一种称为“叶子优先”的树生长策略，LightGBM能够更好地处理过拟合问题，从而提高模型的泛化能力。

支持类别特征：LightGBM可以直接处理类别特征，无需进行独热编码，这可以减少内存占用并加速训练。

可扩展性：LightGBM支持并行学习以及分布式学习，可以处理非常大规模的数据集。

LightGBM的核心技术：

基于直方图的算法：LightGBM使用直方图方法将连续特征分桶，即将特征值划分到不同的区间，从而降低内存消耗。同时，直方图相减技术能够加速子节点的直方图计算，提高训练速度。

叶子优先的树生长策略：传统的GBDT算法采用“深度优先”的树生长策略，即在每一层上尽可能地生长所有节点。而LightGBM采用“叶子优先”的策略，即优先生长那些能够带来最大损失减少的节点。这种策略可以更好地处理过拟合问题，提高模型的泛化能力。

直接处理类别特征：LightGBM能够直接处理类别特征，而无需进行独热编码。它会根据特征值的出现频率自动对类别特征进行排序，然后采用类似于直方图的方式进行分桶。这种方法能够降低内存占用并加速训练。

并行学习和分布式学习：LightGBM支持并行学习和分布式学习，以便在多核处理器或分布式环境中加速训练过程。它使用以下技术实现这一目标：

特征并行：特征并行方法通过划分特征空间来实现并行化。不同的线程或机器负责处理不同的特征子集。这种方法可以加速直方图构建过程，并减少通信开销。
数据并行：数据并行方法通过划分数据集来实现并行化。每个线程或机器负责处理数据集的一个子集。然后将局部直方图汇总以构建全局直方图。这种方法可以同时利用多个处理器的计算能力，进一步提高训练速度。
投票并行：投票并行方法结合了特征并行和数据并行的优势。每个线程或机器负责处理数据集的一个子集，并构建局部直方图。然后通过投票机制选择最佳分割点，以减少通信开销。

自动参数调优：LightGBM提供了许多可以调整的参数，以满足不同问题的需求。通过使用贝叶斯优化等自动参数调优方法，用户可以在不需要深入了解每个参数的情况下，获得更好的模型性能。

总之，LightGBM是一个高效且强大的梯度提升决策树框架。它在许多方面优于其他GBDT算法，如XGBoost。通过使用直方图方法、叶子优先的树生长策略、直接处理类别特征以及并行学习和分布式学习等技术，LightGBM能够在提高训练速度的同时，保持较高的模型准确性。

为了理解直方图梯度提升（Histogram-based Gradient Boosting）的原理，先回顾一下回归决策树的构建过程。在构建回归树时，我们需要遍历所有特征，对于连续型特征，我们需要按特征值排序，并尝试所有可能的分割方法，计算每种分割方法的误差，然后找到误差最小的分割方式作为当前节点的分割方法。

但是，这种方法在处理大量数据时，计算量会随着样本数量和特征维度的增加而大幅度增长。例如，如果我们有100万个样本和100个数值型特征，我们可能需要尝试100亿次计算才能找到一个节点的最佳分割方法，这样的分割方式在大数据量下会导致训练速度很慢。

为了加速训练过程，我们可以采用一种改进方案：对特征值进行分箱处理。假设仍然有100万个样本和100个数值型特征，这时我们将每个特征列分成100个箱子。现在要找到最佳分割点，我们只需进行1万次计算即可，相比原来的方案，计算量最多减少了10000倍。这种方式使得算法更加高效，训练速度更快

import matplotlib.pyplot as plt
import matplotlib.patches as patches
import numpy as np
# 形状：指的是matplotlib.patches 包里面的一些对象，比如我们常见的箭头，正方形，椭圆等等，也称之为“块”。
n_samples = 50
n_bins = 5

X = np.random.uniform(low=-6.0, high=6.0, size=(n_samples,))
X = np.sort(X)
y = 1 / (1 + np.exp(-X))

# 绘制数据
fig, ax = plt.subplots(nrows=1, ncols=3, figsize=(13, 4))
ax[0].scatter(X, y, s=10)
ax[0].set_title('1d regression problem with {0} points'.format(n_samples))
ax[0].set_xlabel('X')
ax[0].set_ylabel('y')

# 绘制标准的分割方式
ax[1].scatter(X, y, s=10)
for i in range(n_samples - 1):
    split = (X[i] + X[i - 1]) / 2
    ax[1].plot([split, split], [0.0, 1.0], c='r', linewidth=1)
ax[1].set_title('Standard: {0} splits to consider'.format(n_samples - 1))
ax[1].set_xlabel('X')
ax[1].set_ylabel('y')

# 找到最佳分割点
best = (-np.inf, np.inf)
for i in range(n_samples - 1):
    split = (X[i] + X[i - 1]) / 2
    loss = np.mean((y[X <= split] - np.mean(y[X <= split])) ** 2) + \
           np.mean((y[X > split] - np.mean(y[X > split])) ** 2)
    if loss <= best[1]:
        best = (split, loss)
print(best)
ax[1].plot([best[0], best[0]], [0., 1.], linewidth=3, linestyle='--', c='k')

ax[2].scatter(X, y, s=10)
splits = [X[0], X[10], X[20], X[30], X[40], X[49]]
for split in splits:
    ax[2].plot([split, split], [0.0, 1.0], c='r', linewidth=1)
bin_colors = ['#8000ff', '#1996f3', '#4df3ce', '#b2f396', '#ff964f', '#ff0000']
for i in range(n_bins):
    ax[2].add_patch(patches.Rectangle((splits[i], 0.0), splits[i + 1] - splits[i], 1.0, color=bin_colors[i], alpha=0.2))
ax[2].set_title('Histogram with {0} bins: {0} splits to consider'.format(n_bins))
ax[2].set_xlabel('X')
ax[2].set_ylabel('counts')

# 找到分箱之后的最佳分割点
best = (-np.inf, np.inf)
splits = [X[0], X[10], X[20], X[30], X[40], X[49]]
for split in splits:
    loss = np.mean((y[X <= split] - np.mean(y[X <= split])) ** 2) + \
           np.mean((y[X > split] - np.mean(y[X > split])) ** 2)
    if loss <= best[1]:
        best = (split, loss)
print(best)
ax[2].plot([best[0], best[0]], [0., 1.], linewidth=3, linestyle='--', c='k')

plt.show()

编辑切换为居中

添加图片注释，不超过 140 字（可选）

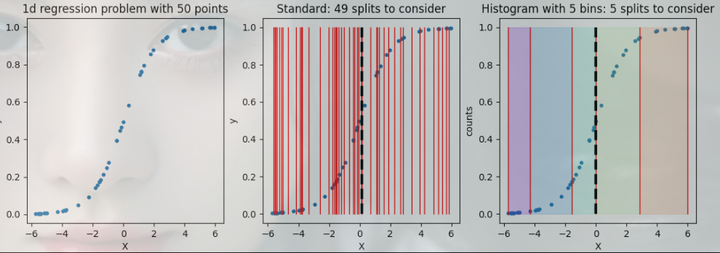
在上面的示例中，我们对比了标准回归树分裂方法和基于直方图的回归树分裂方法。在标准回归树分裂方法中，我们尝试了49种不同的分裂方式，最终找到了最佳分裂点。而在基于直方图的回归树中，我们仅仅尝试了4次就找到了最佳分裂方式。这意味着，如果数据规模变得更大，使用基于直方图的回归树方法训练速度会更快

from sklearn.ensemble import HistGradientBoostingClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split

X, y = load_breast_cancer(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=45)

histGBC = HistGradientBoostingClassifier(max_depth=2, max_iter=20, learning_rate=0.75)
histGBC.fit(X_train, y_train)
histGBC_score = histGBC.score(X_test, y_test)
print('Histogram Gradient Boosting Classifier Accuracy:', histGBC_score)

GOSS（Gradient-based One Side Sampling）

减少参与模型训练的样本数量可以提高模型训练的速度。在之前学习过的模型中，我们通常是通过随机采样的方式实现的， LightGBM采用了另一种采样方式基于梯度的单边采样：根据样本梯度来对梯度小的样本（单边）进行采样，而对梯度大的样本保留

单边的含义：梯度大的是一边，梯度小的是另一边

举例: 训练数据1000w，一部分数据做采样, 另一部分不做采样

梯度最大的前10%的数据不采样, 剩下的90%的数据进行采样, 采样200w条, 这

样得到300w条数据，大大降低了训练过程的计算量

问题，对梯度较小的部分是否要放弃：完全舍弃会改变样本的分布，影响模型效果

为了减小采样带来的对数据分布的影响，对采样的部分乘上一个权重，权重的计算

方法 W = (100-a)/b

a% 为不采样的部分占全部数据的百分比，b%为采样部分的采样比例

比如梯度最大的前10%不采样，剩下的部分采样30% 则 W = (100-10)/30 = 3

以下是采用GOSS算法进行训练的简化步骤：

1根据当前模型进行预测，得到样本的预测值。

2根据预测值计算损失，得到梯度g，将样本权重w初始化为1。

3按照梯度g的绝对值降序排序，得到一个样本索引数组。

4选取梯度最大的前topN（a × len(I)）个样本，得到索引数组topSet。

5在剩余样本中随机选择randN（b × len(I)）个小梯度样本，得到索引数组randSet。

6合并topSet和randSet，得到一个新的索引数组usedSet，其大小为（a+b）× len(I)。

7更新小梯度样本的权重，乘以权重系数因子 1-a/b，得到新的样本权重w。

8根据usedSet索引的样本、梯度g和权重w，训练一个新的弱学习器newModel。

9将新的弱学习器newModel加入总模型。

实验表明，采用GOSS算法后，模型性能没有下降，反而有所提升。这是因为采样增加了弱学习器的多样性，从而提高了模型的泛化能力。

EFB（互斥特征捆绑）方法是从特征角度出发，降低数据的维度。GOSS解决了大量样本的采样问题，而EFB主要针对特征。

它的典型应用场景是处理类别特征的one-hot编码。

例如，一个类别型变量有10个不同的取值，经过one-hot编码后，该变量会变成10维特征，其中只有一个是非零的，其他的都是零。

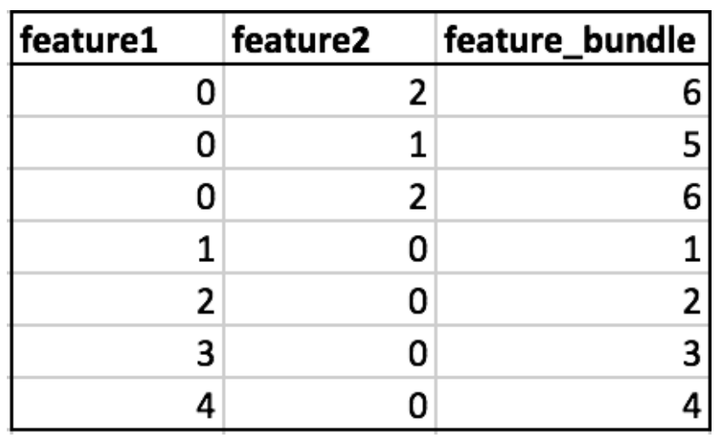
EFB的核心思想是将冲突较小的特征捆绑在一起，降低数据的维度。具体操作如下：

首先计算要添加到特征包（bundle）中每个特征的偏移量。

然后迭代每个数据实例和特征。

对于所有特征都为零的实例，将其放入值为0的箱中。

对于每个特征的非零实例，计算新的分箱值 = 特征原始值 + 偏移量。

通过这种方式，EFB能够将冲突较小的特征捆绑在一起，从而降低数据维度，提高模型训练速度。

rom sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
X, y = load_breast_cancer(return_X_y=True)
Xtrn, Xtst, ytrn, ytst = train_test_split(X, y, test_size=0.2,random_state=45)
# 模型训练
from lightgbm import LGBMClassifier
gbm = LGBMClassifier(boosting_type='gbdt', n_estimators=20,max_depth=1,learning_rate=0.75)
gbm.fit(Xtrn, ytrn)
# 模型评估
from sklearn.metrics import accuracy_score
ypred = gbm.predict(Xtst)
accuracy_score(ytst, ypred)

早停

import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from lightgbm import LGBMClassifier

X, y = np.random.rand(1000, 20), np.random.randint(0, 2, 1000)

# 数据划分
Xtrn, Xval, ytrn, yval = train_test_split(X, y, test_size=0.2, random_state=42)

number_of_steps = np.arange(1, 10, 1)
trn_err = np.zeros((len(number_of_steps), ))
val_err = np.zeros((len(number_of_steps), ))
n_iters = np.zeros((len(number_of_steps), ))

for i, rounds in enumerate(number_of_steps):
    gbm = LGBMClassifier(boosting_type='gbdt', n_estimators=50,
                         max_depth=1, early_stopping_rounds=rounds)
    gbm.fit(Xtrn, ytrn, eval_set=[(Xval, yval)],
            eval_metric='auc', verbose=False)
    trn_err[i] = 1 - accuracy_score(ytrn, gbm.predict(Xtrn))
    val_err[i] = 1 - accuracy_score(yval, gbm.predict(Xval))
    n_iters[i] = len(gbm.evals_result_['valid_0']['auc'])

print("Training Error:", trn_err)
print("Validation Error:", val_err)
print("Number of Iterations:", n_iters)

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(9, 4))
ax[0].plot(number_of_steps, trn_err, marker='o',
markeredgecolor='w', linewidth=2)
ax[0].plot(number_of_steps, val_err, marker='s',
markeredgecolor='w', linewidth=2)
ax[0].legend(['Train err', 'Validation err'])
ax[0].set_xlabel('early_stopping_rounds')
ax[0].set_ylabel('Error (%)')
ax[0].set_xticks(range(10))
ax[1].plot(number_of_steps, n_iters, marker='o',
markeredgecolor='w', linewidth=2)
ax[1].set_xlabel('early_stopping_rounds')
ax[1].set_ylabel('Ensemble size at early stopping')
ax[1].set_xticks(range(10))
plt.show()

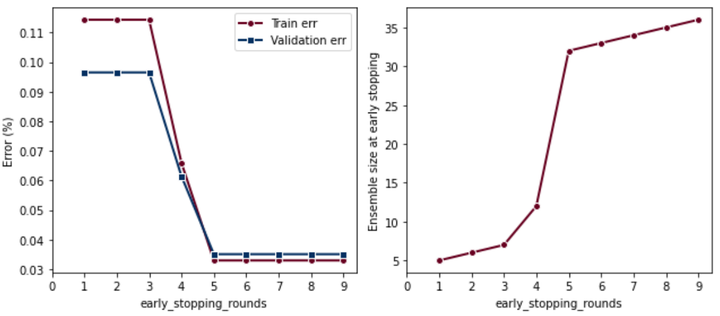
早停设置太小会欠拟合

Hitogram算法的主要作用是减少候选分裂点数量

GOSS算法的作用是减少样本的数量

EFB算法的作用是减少特征的数量。

LightGBM（Light Gradient Boosting Machine）是一种基于梯度提升（Gradient Boosting）框架的决策树集成学习算法。与其他梯度提升算法相比，LightGBM在速度和内存使用上具有明显优势，同时保持了较高的精度。在本次回答中，我们将详细介绍LightGBM的数学推导过程。

基于残差的学习：

给定训练数据集 D = {(x1, y1), (x2, y2), ..., (xn, yn)}，其中 xi 是特征向量，yi 是对应的目标值。我们希望通过学习得到一个模型 F(x)，使得损失函数 L(y, F(x)) 最小化。

对于梯度提升算法，我们通过迭代地构建弱学习器（通常为决策树），并将其加入到最终的预测模型中。在第 t 次迭代中，我们将学习一个弱学习器 ht，更新模型 F_t(x) = F_{t-1}(x) + ht(x)。我们希望最小化损失函数 L(y, F_t(x))。

损失函数的泰勒展开：

L(y, F_t(x)) ≈ L(y, F_{t-1}(x)) + (y - F_{t-1}(x)) * ht(x) + 0.5 * (y - F_{t-1}(x))^2 * h_t(x)^2

在这里，我们忽略了高阶项。我们的目标是找到一个最优的弱学习器 h_t(x)，使得损失函数最小化。由于一阶导数项 (y - F_{t-1}(x)) 是关于 h_t(x) 的线性项，我们可以将其视为负梯度，表示损失函数在当前模型 F_{t-1}(x) 处下降的最快方向。因此，我们的目标是学习一个弱学习器 h_t(x)，使得它能够拟合负梯度 (y - F_{t-1}(x))。

Leaf-wise的决策树生长策略：

LightGBM 使用了一种叫做 Leaf-wise 的决策树生长策略。与 Level-wise 策略相比，Leaf-wise 策略每次分裂都选择具有最大信息增益的叶子节点，因此可以更快地减小损失函数。

在每次分裂时，我们需要在所有叶子节点中选择一个最优的分裂特征。对于第 i 个叶子节点，假设它包含的样本索引集合为 I_i。我们需要找到一个特征 j 和一个分裂点 s，使得损失函数最小化。

损失函数可以表示为：

L = L_left + L_right

其中 L_left 和 L_right 是分裂后的左子树和右子树的损失函数。为了找到最佳的特征 j 和分裂点 s，我们需要计算每个特征和分裂点的信息增益 G：

G = L_before_split - L

在具体计算信息增益时，LightGBM 使用了一种更高效的方法。对于每个特征 j，我们可以计算其对应的梯度 g_j 和 hessian h_j：

Hessian（海森矩阵）h_j 是二阶导数矩阵的简化形式。LightGBM 是一种基于梯度提升（Gradient Boosting）的机器学习算法，它在训练决策树模型时考虑了损失函数的一阶导数（梯度）和二阶导数（海森矩阵）来加速训练过程。

在 LightGBM 中，对于特征 j，梯度 g_j 表示损失函数相对于该特征的一阶导数，而 hessian h_j 表示损失函数相对于该特征的二阶导数。这些梯度和海森矩阵值用于在每一轮迭代中找到最佳的分裂点，以便在构建决策树时最大限度地降低损失函数。海森矩阵 h_j 有助于更准确地估计特征分裂对损失函数的影响，从而提高模型性能。

简而言之，h_j（Hessian）是损失函数相对于特征 j 的二阶导数，它用于在 LightGBM 算法中更精确地估计特征分裂的影响。

g_j = Σ_{i∈I}(y_i - F_{t-1}(x_i))

h_j = Σ_{i∈I}(2 * (y_i - F_{t-1}(x_i)))

然后我们可以用这些梯度和 hessian 计算信息增益 G：

G = 0.5 * (g_left^2 / (h_left + λ) + g_right^2 / (h_right + λ) - g_all^2 / (h_all + λ))

其中 λ 是正则化参数。

直方图优化：

为了进一步提高计算效率，LightGBM 使用了直方图优化方法。对于连续特征，我们可以将其离散化为 b 个桶，每个桶对应一个特征值范围。对于每个桶，我们可以计算对应的梯度和 hessian 的累积和。这样，在计算信息增益时，我们可以直接使用这些累积和，从而大大减少计算量。

特征并行与数据并行：

LightGBM 支持特征并行和数据并行，以实现在多台机器上进行分布式训练。特征并行的主要思路是将特征空间划分到不同的机器上，并在每台机器上计算局部的信息增益。然后通过通信找到全局最优的分裂特征。数据并行的主要思路是将数据划分到不同的机器上，并在每台机器上构建局部的直方图。然后通过通信合并这些局部直方图，得到全局直方图，从而找到最优的分裂特征。

通过以上方法，LightGBM 能够在保持高精度的同时，显著提高训练速度和内存效率。

类别特征处理：

LightGBM 可以自动处理类别特征，而无需进行独热编码（One-Hot Encoding）。对于类别特征，LightGBM 将其映射到整数值。在构建决策树时，LightGBM 使用了一种特殊的分裂策略，称为 Optimal Split for Categorical Features（类别特征的最优分裂）。该策略通过找到一个最佳的类别组合，将类别特征划分为两个子集，从而使得信息增益最大化。

正则化：

为了防止过拟合，LightGBM 提供了多种正则化方法。其中包括：

L1 和 L2 正则化：用于正则化叶子节点的输出值。在计算损失函数时，我们可以在分子中添加 L1 正则化项 (α|w|) 和/或 L2 正则化项 (0.5*λw^2)。
最大树深度：限制决策树的最大深度，以控制模型的复杂度。
最小数据量：限制叶子节点中的最小数据量，以防止过拟合。
最大叶子节点数：限制决策树的最大叶子节点数，以控制模型的复杂度。

早停策略：

LightGBM 支持使用早停策略来防止过拟合。在训练过程中，我们可以设置一个验证集，用于监控模型在每轮迭代后的性能。如果在一定轮数的迭代中，验证集上的性能没有明显改善，我们可以提前终止训练，从而节省计算资源。

随机性引入：

为了降低过拟合风险，LightGBM 可以在训练过程中引入随机性。主要包括：

列采样（Feature Subsampling）：在每轮迭代中，随机选择一部分特征用于训练。
行采样（Data Subsampling）：在每轮迭代中，随机选择一部分数据用于训练。

通过以上介绍，您可以了解到 LightGBM 是如何通过各种优化策略和技巧，在保持高精度的同时，实现高效的训练过程。

多分类问题：

LightGBM 支持多分类问题。对于多分类问题，LightGBM 使用 Softmax 函数将模型的输出转换为每个类别的概率值。在这种情况下，损失函数是多分类的对数损失。对于多分类问题，LightGBM 需要训练 k 个二元分类器（k 是类别数目），每个分类器对应一个类别。在训练过程中，梯度和 Hessian 的计算会针对多分类问题进行调整。

自定义目标函数和评估指标：

LightGBM 提供了接口，允许用户定义自己的目标函数和评估指标。自定义目标函数需要计算损失函数的一阶和二阶梯度。自定义评估指标需要计算预测结果与实际目标值之间的误差。

模型解释：

LightGBM 提供了一些方法来解释模型的预测结果。例如：