原理

在探测远距离目标时，由于目标回波信号比较微弱，信号幅度很小，从而导致接收信号的信噪比（SNR）过低，以至于信号处理算法检测不到目标，从而发生漏检。

在脉冲体制雷达中，雷达系统通常采用对脉冲回波样本进行脉冲积累这一基本操作来提高 SNR，从而提升雷达系统的检测性能。脉冲积累方式主要包括两种：相参积累和非相参积累。

相参积累是指对复数数据（即，含有幅度和相位信息）进行累积，而非相参积累只指对信号的幅度（它可以是幅度的不同表示形式 ，例如幅度的平方或幅度的对数值）进行累积，即信号包络简单相加。

同等条件下，对回波信号进行相参积累后的信噪比要好于非相参积累，原因是非相参积累方式损失了回波信号的相位信息。但相参脉冲积累处理实现起来比非相参脉冲积累复杂得多。虽然非相参积累方式在实现方面比较简单，但由于其积累增益总是小于积累脉冲数，回波信号的信噪比相对于相参积累损失较多，不如相参积累算法有效。

设雷达发射的是线性调频脉冲信号，发射能量只有一部分被反射回来。中频信号从接收机输出，输出信号中包含复包络为 $A{e}^{i\varphi }$ 的复回波信号，以及加性噪声 $w$ 。假设在通带中噪声是功率为 ${\sigma }^2$ 的随机过程，一个单脉冲的信噪比被定义为：$$X_1=\frac{信号功率}{噪声功率}=\frac{A^2}{{\sigma }^2}.$$设测量又重复了 $N–1$ 次，即在同一个方位上发射了相同的 $N$ 个脉冲。假定观测的回波响应是相同的，而且每次观测的噪声样本是独立的。最后，这些回波信号的观测值将被累计（相加），以产生一个新的观测值 $z$，其对复信号样本的求和过程即相参积累过程： z = ∑ n = 0 N − 1 { A e i Φ + w [ n ] } = N A e i ϕ + ∑ i = 0 N − 1 w [ n ] . z=\sum_{n=0}^{N-1}\{ Ae^{i\Phi}+w[n] \}=NAe^{i\phi}+\sum_{i=0}^{N-1}w[n]. z=n=0∑N−1​{AeiΦ+w[n]}=NAeiϕ+i=0∑N−1​w[n].显然，能量累积后信号能量为 $N^2{A}^2$，上式中的 $w[n]$ 为噪声样本函数。

如果噪声样本是独立且零均值的，则噪声的总功率是各噪声独立样本的功率之和。进一步假设，噪声样本都服从相同的统计分布，功率都为 ${\sigma }^2$ ，则总噪声功率为 $N{\sigma }^2$ ，积累之后的信噪比变为：$$X_N=\frac{N^2{A}^2}{N{\sigma }^2}=N\frac{A^2}{{\sigma }^2}=N{X}_1.$$从上述推导结果可以看出，将 N 次独立的观测值进行相参积累后，回波信号的 SNR 得以提高到原来单脉冲回波的 N 倍，提高的信噪比称为积累增益。

在雷达信号处理过程中，提高回波的 SNR 可以改善雷达的目标检测和参数提取性能，但其代价是连续积累了 N 个脉冲的信号。

在对回波信号相参积累的过程中，信号分量是同相相加，即相参相加。由于 $N$ 个脉冲积累后的总的信号幅度是单个脉冲信号幅度的 $N$ 倍，因此，积累后总的信号的能量变为单个脉冲信号的能量的 $N^2$ 倍。而对于噪声分量，由于其相位是随机变化的，所以积累后噪声总能量为功率相加。由于回波信号的相位是一致的，所以才使得信号能量积累的增长高于噪声能量积累的增长。

距离徙动及其补偿方法

在脉冲体制雷达中，如果待检测的目标运动速度很大，或者相参积累时间很长，回波信号可能会出现跨距离单元走动现象，从而影响雷达检测性能。

设脉冲雷达发射的基带信号为：$$u(t)=rect(\frac{t}{T})e^{i\pi K{t}^2}$$其中， $T$ 为脉冲宽度， $K$ 为 chirp 信号的调频率。
第 m 个发射脉冲的回波信号为：$$S_m(\hat{t},t_m)=u(\hat{t}-\frac{2R_m}{c})e^{-j\frac{4\pi f_c}{c}{R}_m}$$其中，$\hat{t}=t-m{T}_r$ 表示脉内时间；$t_m=m{T}_r,m=0,1,...,M-1$，为脉冲慢时间， $M$ 为相参积累脉冲数， $T_r$ 为脉冲重复周期； $f_c$为载波频率； $R_m$ 为发射第 $m$ 个脉冲时雷达与目标之间的距离，$R_m=R_0-v{t}_m$（$v$ 大于0，表示目标向雷达靠近）。
根据驻相原理，发射的线性调频信号的频谱为：$$U(f)=rect(\frac{f}{B})e^{-j\frac{\pi f^2}{K}}.$$则每个脉冲回波脉压后的频谱为：$$Y(f,m)=rect(\frac{f-f_{d/2}}{B-|f_d|})e^{-j\frac{\pi {f_d}^2}{K}}{e}^{-j2\pi f(\eta (m)-f_d/K)}{e}^{-j2\pi (-f_d+f_c)\eta (m)}$$其中，$\eta (m)=2\frac{R_m}{c}={\eta }_0-2\frac{v{t}_m}{c},f_d=\frac{2v{f}_c}{c}$ 为目标的多普勒频率，其脉压后时域信号为：$$y(\hat{t},m)=(B-|f_d|)\sin c[(B-|f_d|)(\hat{t}-\eta (m)+\frac{f_d}{K})]e^{j\pi {f_d}^2}{e}^{j\pi f_d\eta (m)}{e}^{-j2\pi f_d{\eta }_0}{e}^{j\pi f_{d}m{T}_r}.$$可以看出，距离维脉压后的信号包络为 sinc 函数，则可知，第 $m$ 个脉冲的峰值位置在 $\hat{t}=\eta (m)-\frac{f_d}{K}$ 处。由此可见，各个回波脉冲的峰值位置不同，即产生了距离徙动。

常用的回波信号距离徙动补偿方法是 Keystone 变换，其实现方法主要有三种：

Keystone变换是一种用于雷达信号距离徙动补偿的变换方法，能够消除距离徙动对回波信号的影响，提高雷达系统的性能。
Keystone变换的基本思路是将接收到的回波信号在频域上旋转一定的角度，然后再通过逆变换得到补偿后的信号。这个旋转角度可以通过距离徙动的大小和方向来确定。

1）DFT+IFFT方法：该方法先对接收到的回波信号进行DFT变换，得到频域上的信号，然后将频域信号旋转一定的角度（根据距离徙动的大小和方向决定），最后对旋转后的信号进行IFFT变换，得到时域上的信号，即为经过距离徙动补偿后的信号。这种方法实现简单，但需要大量的计算。

2）SINC内插方法：该方法利用SINC函数进行内插，将采样率提高到一个很大的值，然后对采样率提高后的信号进行FFT变换，得到频域信号，接着将频域信号旋转一定的角度，最后对旋转后的信号进行IFFT变换，得到时域上的信号，即为经过距离徙动补偿后的信号。这种方法需要较少的计算量，但对信号的高频成分会有一定的失真。

3）Chirp-Z变换方法：该方法将接收到的回波信号转化为一系列chirp信号，然后利用Chirp-Z变换进行距离徙动补偿。这种方法的计算量较小，但需要进行信号分段处理，且对信号的波形有一定的限制。

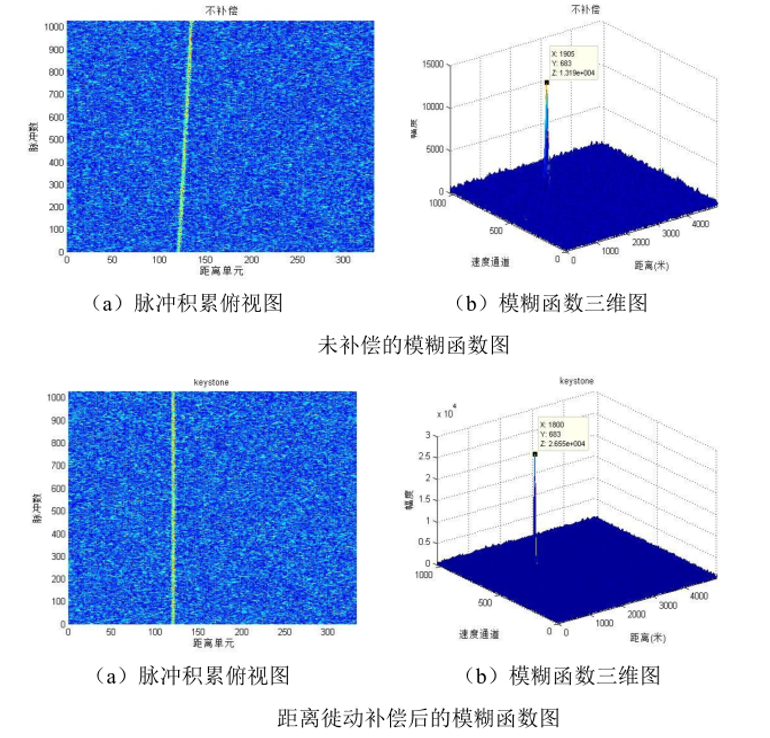
频率徙动法及其补偿方法

考虑目标的运动对相参积累的影响，长时间相参积累时目标的径向加速度会导致传统的信号处理技术在多普勒维产生徙动，使目标能量分散到多个多普勒单元，降低目标回波的信噪比，导致雷达检测性能大幅下降。

频率徙动（Frequency Modulation）是指当目标在运动时，由于其速度在不断变化，导致接收到的信号频率也随之发生变化的现象。与距离徙动不同的是，频率徙动并不受到目标与雷达天线之间距离的影响，而主要受到目标速度的影响。具体来说，当目标速度增大时，接收到的信号频率会增大；当目标速度减小时，接收到的信号频率会减小。

频率徙动的原理可以通过多普勒效应来解释，多普勒效应是指当发射源和接收器相对于运动目标移动时，接收到的信号频率会发生变化的现象。如果运动目标远离雷达系统，回波信号频率将比发射时低；如果运动目标靠近雷达系统，回波信号频率将比发射时高。这种频率变化与目标的速度和方向有关，因此可以通过测量回波信号的频率变化来获得目标的运动信息。

加速度的存在将导致目标回波的多普勒频率出现徙动，从而影响目标检测，为减少或消除多普勒徙动对信号检测的影响，脉冲积累检测之前需要对其进行补偿。

如果不进行补偿，这种频率变化将影响雷达系统的性能，导致距离、速度等参数的测量误差增大，甚至导致目标无法被正确探测。

在雷达信号处理中，为了消除频率徙动对回波信号的影响，常常需要对接收到的信号进行频率徙动补偿。常用的方法包括采用基于Chirp信号的距离-速度二维FFT方法和采用基于Keystone变换的频率徙动补偿方法等。这些方法可以对接收到的信号进行处理，消除频率徙动对回波信号的影响，提高雷达系统的性能。