海量数据面试题

在这里插入图片描述

文章目录

海量数据面试题
一、哈希切割
二、位图应用
- 1.给定100亿个整数，设计算法找到只出现一次的整数
- 2.求两个文件交集
- 3.在100亿个整数中找到出现次数不超过2次的所有整数
三、布隆过滤器
- 1.求两文件交集（近似算法）
- 2.求两文件交集（精确算法）
- 3.计数法使布隆过滤器支持删除

一、哈希切割

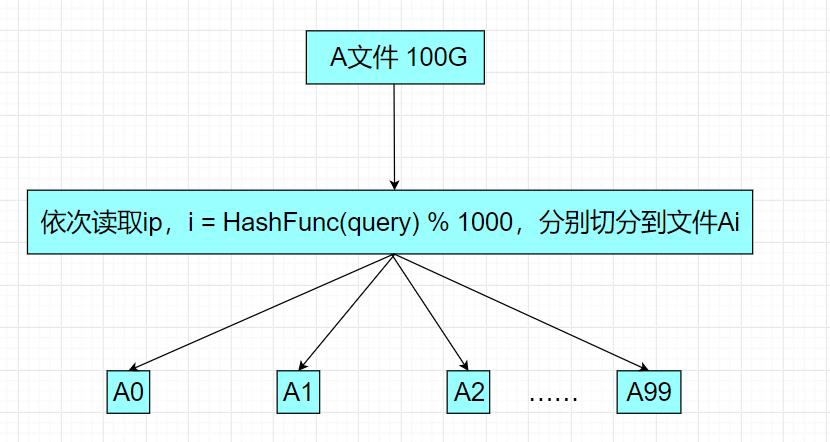
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址？以及如何找到top K的IP？如何直接用Linux系统命令实现？

我们可以把这100G大小的文件切分成100个小文件
依次读取ip地址，通过哈希函数把每个ip地址转换为一个整型，再把这些分别%100切分到这100个小文件里头

此时相同的ip地址通过哈希函数转换的整型一定是相同的，最终也一定进入同一个文件，不同的ip也可能进入同一个文件，现在我们使用map容器（map<string, int> countMap）依次对每个小文件统计次数，统计完A0，把A0的次数记录下来为最大次数（pair<ip, int> maxIP），clear旧数据，再统计A1，比较A1的次数和最大次数的大小，更新最大次数，再clear掉旧数据……，依次比较，依次更新最大次数的数据。
如果需要找到top K，就需要用到优先级队列（priority_queue<pair<string,int>,vector<pair<string,int>>，less>），less仿函数将比较pair中int的大小，使用小堆可满足找最大的K个值的条件。

使用上述哈希切割的方法可以找到出现次数最多的IP地址，但是会存在一个小问题：某个文件太大，导致某个相同ip太多，且映射冲突到这个编号文件的ip太多（可能又会导致内存不够了），这里我们可以try-catch捕获，伪代码如下：
try
{
	countMap[ip]++;
}
catch (exception& e)
{
	//捕获内存不足的异常，说明内存不够
	countMap.clear();
	//针对这个小文件，再次换个哈希函数，进行哈希切分，再切分成小文件
	//再对小文件依次统计
}
找到topK的Linux的指令如下：

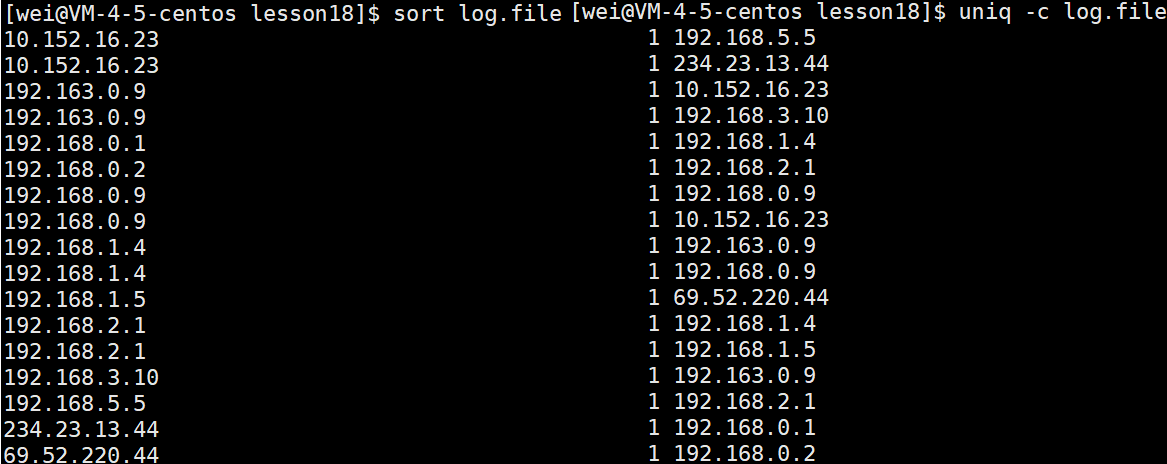
假如有以下文件IP.log：
192.168.5.5
234.23.13.44
10.152.16.23
192.168.3.10
192.168.1.4
192.168.2.1
192.168.0.9
10.152.16.23
192.163.0.9
192.168.0.9 
69.52.220.44 
192.168.1.4 
192.168.1.5
192.163.0.9 
192.168.2.1
192.168.0.1
192.168.0.2
（1）按行排序，并将结果输出到标准输出
sort 文件名
（2）统计并显示文本文件中出现的行或列的次数
uniq -c
（3）根据出现次数倒序排序
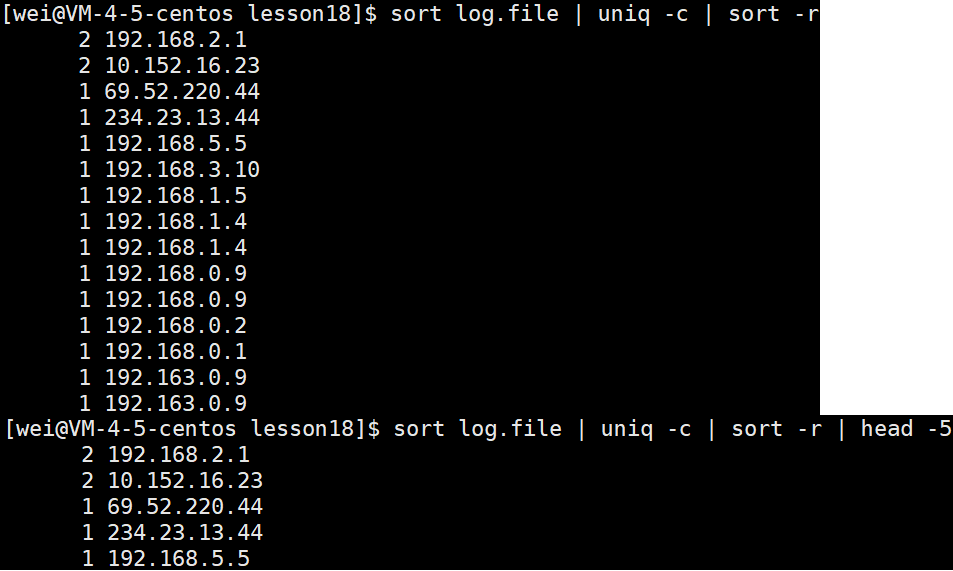
sort -r
（4）查看开头K行
head -k
综上：显示出现次数最多的前K个IP
sort log_file | uniq -c | sort -nr | head -k
sort log_file对文件进行排序，使得相同的IP地址聚在一起，接着使用uniq -c进行去重，并将重复的次数显示在每列的旁边，通过这个次数来使用sort -nr进行降序排序，使得出现次数最高的IP地址在前面，然后使用head -k获取前k个IP地址。

运行结果：

二、位图应用

1.给定100亿个整数，设计算法找到只出现一次的整数

给定100亿个整数，设计算法找到只出现一次的整数

题目明确说找到只出现一次的整数，那说明一个整数出现的次数的情况分为如下三种状态：

出现0次
出现1次
出现2次及以上

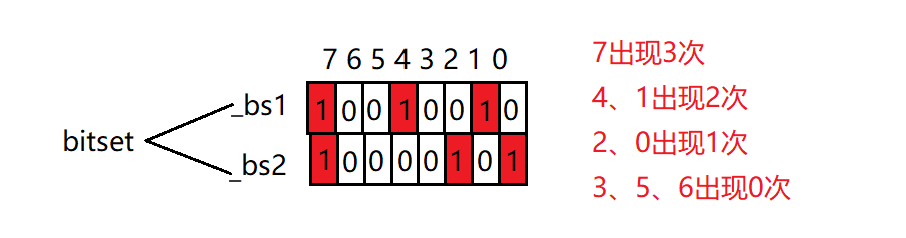
一个比特位只能表示一种状态，但是两个比特位就能表示4种了，因此我们借助两个比特位来表示如上三种状态：

00（0次）
01（1次）
10（2次）

所以这里我们需要重新写一个位图，两个比特位表示一个值，所以一个char只能表示4个值（8bit / 2），100亿个整数要开2^32 * 2个比特位，大概占1G。

虽然这里是两个比特位表示一个值，不过我们实际操作的时候可以设计一个类，里面封装两个bitset，并且通过后续的位运算来表示两个比特位表示一个值。

具体实现的代码如下：
template<size_t N>
class twobitset
{
public:
	void set(size_t x)
	{
		if (!_bs1.test(x) && !_bs2.test(x)) // 00
		{
			_bs2.set(x); // 01
		}
		else if (!_bs1.test(x) && _bs2.test(x)) // 01
		{
			_bs1.set(x); 
			_bs2.reset(x); // 10
		}

		// 10 不变
	}

	void PirntOnce()
	{
		for (size_t i = 0; i < N; ++i)
		{
			if (!_bs1.test(i) && _bs2.test(i))
			{
				cout << i << endl;
			}
		}
		cout << endl;
	}
private:
	bitset<N> _bs1;
	bitset<N> _bs2;
};
简易测试代码如下：
void test_twobitset()
{
	twobitset<100> tbs;
	int a[] = { 3, 5, 6, 7, 8, 9, 33, 55, 67, 3, 3, 3, 5, 9, 33 };
	for (auto e : a)
	{
		tbs.set(e);
	}
	tbs.PirntOnce();
}

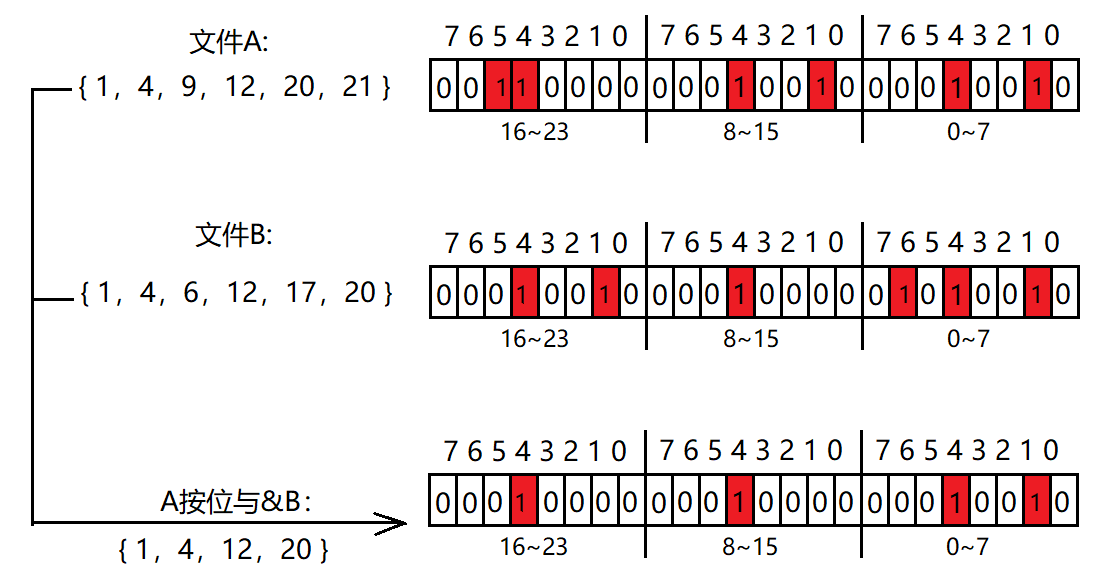
2.求两个文件交集

给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？

这里我们可以设计两个位图，刚好占用1G内存，按照如下方式设置

把A文件读到位图1，把B文件读到位图2
遍历两个位图，将位图1和位图2进行与&操作，结果存储在位图1中，此时位图1中映射的整数就是两个文件的交集。

3.在100亿个整数中找到出现次数不超过2次的所有整数

1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数

此题和第一题的思想是一样的，对于出现的次数，可以用两个比特位来表示，一次表示出现次数的状态：

出现0次（00）
出现1次（01）
出现2次（10）
出现3次及以上（11）

这里同样需要两个位图来解决，只需要对第一题的代码进行改造即可，最后状态是01或10的整数就是出现次数不超过2次的整数。
template<size_t N>
class two_bitset
{
public:
	void set(size_t x)
	{
		int in1 = _bs1.test(x);
		int in2 = _bs2.test(x);
		if (in1 == 0 && in2 == 0)//00
		{
			_bs2.set(x);//01
		}
		else if (in1 == 0 && in2 == 1)//01
		{
			//出现次数置为2
			_bs1.set(x);//10
			_bs2.reset(x);
		}
		else if (in1 == 1 && in2 == 0)//10
		{
			_bs2.set(x);//11
		}
	}
private:
	bitset<N> _bs1;
	bitset<N> _bs2;
};

三、布隆过滤器

1.求两文件交集（近似算法）

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？给出近似算法

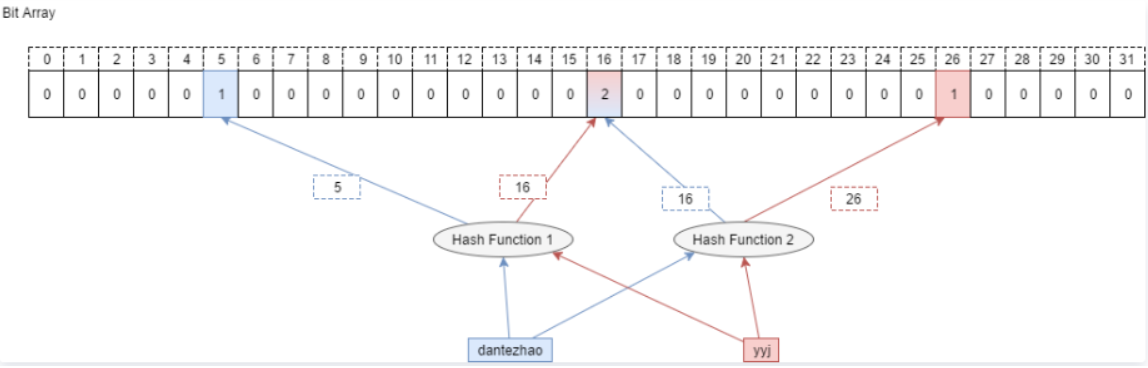
题目要求给出近视算法，也就是允许存在一些误判，那么我们就可以用布隆过滤器。

先读取其中一个文件当中的query，将其全部映射到一个布隆过滤器当中。
然后读取另一个文件当中的query，依次判断每个query是否在布隆过滤器当中，如果在则是交集（但是会存在误判的风险，不过无法避免，这也是近似算法的特点），不在则一定不是交集。

2.求两文件交集（精确算法）

给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？给出精确算法

注意：

这里明确指出给出精确算法，我们不能使用布隆过滤器，因为会存在误判，要用上文一开始使用的哈希切分来解决。

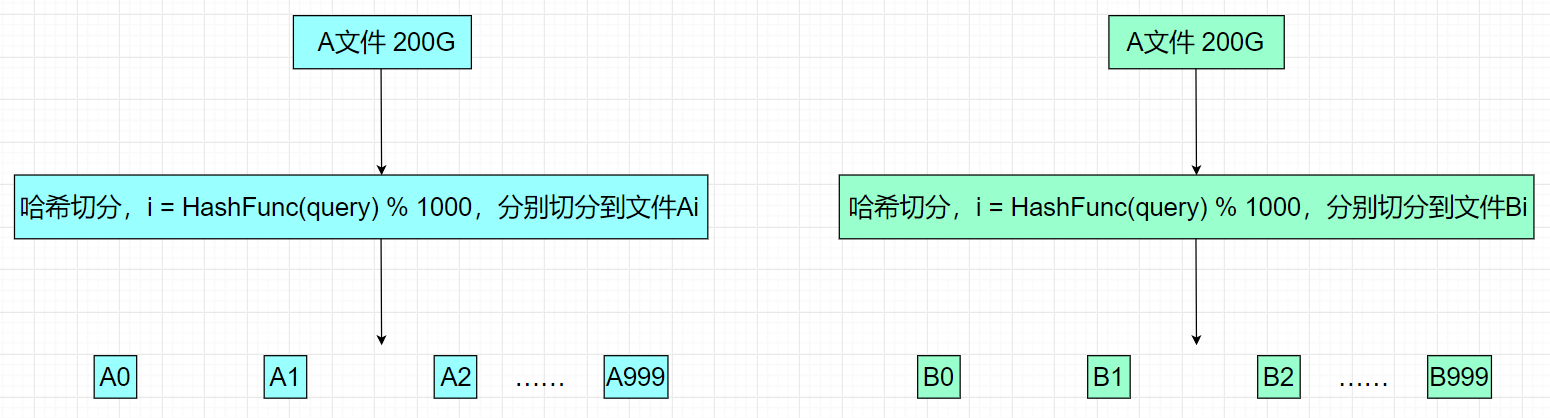
我们按照如下的规则来进行哈希切割。

我们假设每个query平均20byte，100亿query就是200G，我们可以把这么个文件分为1000个小文件
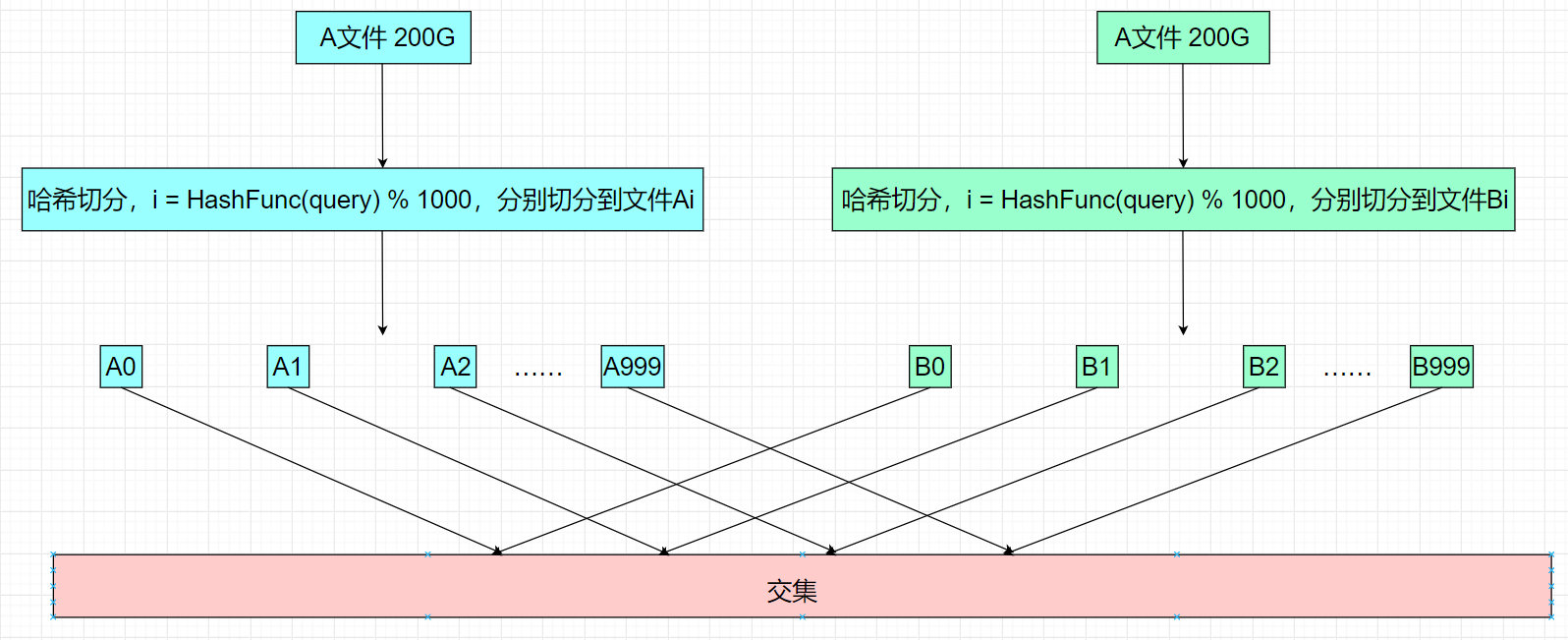
依次读取query，通过哈希函数把每个query转换为一个整型，再把这些分别%1000切分到这1000个小文件里头，此时文件A就被分为A0 ~ A999共1000个小文件，文件B就被分为B0 ~ B999共1000个小文件。

由于在切分A文件和B文件的时候，使用的是相同的哈希函数，因此A文件和B文件中相同的query计算的是相同的i值，就被分到了对应的Ai和Bi中，因此我们只需要找到A0与B0的交集、A1与B1的交集……最终把这些集合合并起来就是文件A和文件B的总交集。

而小文件找交集的方法也很简单，如下规则：

我们可以将其中一个小文件加载到内存，并放到一个set容器中，再遍历另一个小文件当中的query，依次判断每个query是否在set容器中，如果在则是交集，不在则不是交集。
如果切分出来的一个小文件过大，需要将此文件再次进行切分，再走一遍这个过程即可。

3.计数法使布隆过滤器支持删除

如何扩展BloomFilter使得它支持删除元素的操作？

布隆过滤器不能直接支持删除工作，因为在删除一个元素时，可能会影响其他元素。一种支持删除的方法（计数法删除）：

将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储空间的代价来增加删除操作。

缺陷：

无法确认元素是否真正在布隆过滤器中
存在计数回绕

总结：

布隆过滤器不支持直接删除归根结底在于其主要就是用来节省空间和提高效率的，在计数法删除时需要遍历文件或磁盘中确认待删除元素确实存在，而文件IO和磁盘IO的速度相对内存来说是很慢的，并且为位图中的每个比特位额外设置一个计数器，就需要多用原位图几倍的存储空间，这个代价也是不小的。若支持删除就不那么节省空间了，也就违背了布隆过滤器的本质需求。