标准差

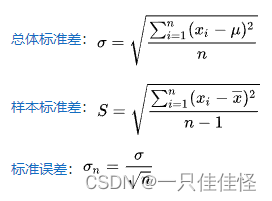
标准差（Standard Deviation）是离均差平方的算术平均数（即：方差）的算术平方根。
标准差是方差的算术平方根。标准差能反映一个数据集的离散程度。平均数相同的两组数据，标准差未必相同。

计算公式：

一、语法

1、S = std(A) 返回 A 沿大小不等于 1 的第一个数组维度的元素的标准差。

如果 A 是观测值的向量，则标准差为标量。
如果 A 是一个列为随机变量且行为观测值的矩阵，则 S 是一个包含与每列对应的标准差的行向量。
如果 A 是多维数组，则 std(A) 会沿大小不等于 1 的第一个数组维度计算，并将这些元素视为向量。此维度的大小将变为 1，而所有其他维度的大小保持不变。
默认情况下，标准差按 N-1 实现归一化，其中 N 是观测值数量。

2、S = std(A,w) 为上述任意语法指定一个权重方案。当 w = 0 时（默认值），S 按 N-1 进行归一化。当 w = 1 时，S 按观测值数量 N 进行归一化。w 也可以是包含非负元素的权重向量。在这种情况下，w 的长度必须等于 std 将作用于的维度的长度。
当 w 为 0 或 1 时，S = std(A,w,‘all’) 计算 A 的所有元素的标准差。此语法适用于 MATLAB® R2018b 及更高版本。

3、S = std(A,w,dim) 使用上述任意语法沿维度 dim 返回标准差。要维持默认归一化并指定操作的维度，请在第二个参数中设置 w = 0。

当 w 为 0 或 1 时，S = std(A,w,vecdim) 计算向量 vecdim 中指定维度的标准差。例如，如果 A 是矩阵，则 std(A,0,[1 2]) 计算 A 中所有元素的标准差，因为矩阵的每个元素包含在由维度 1 和 2 定义的数组切片中。

4、S = std(___,nanflag) 指定在上述任意语法的计算中包括还是忽略 NaN 值。例如，std(A,‘includenan’) 包括 A 中的所有 NaN 值，而 std(A,‘omitnan’) 则会忽略这些值。

二、举例

1、矩阵列的标准差

创建一个矩阵，并计算每一列的标准差。

A = [4 -5 1; 2 3 5; -9 1 7];
S = std(A)

S = 1×3
7.0000 4.1633 3.0551

2、三维数组的标准差

创建一个三维数组，并计算沿第一个维度的标准差。

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
S = std(A)

S =
S(:,:,1) =
2.8284 2.1213
S(:,:,2) =
9.8995 4.2426
S(:,:,3) =
2.8284 4.9497

3、指定标准差权重

创建一个矩阵，并根据权重向量 w 计算每一列的标准差。

A = [1 5; 3 7; -9 2];
w = [1 1 0.5];
S = std(A,w)

S = 1×2
4.4900 1.8330

4、矩阵行的标准差

创建一个矩阵，并计算每一行的标准差。

A = [6 4 23 -3; 9 -10 4 11; 2 8 -5 1];
S = std(A,0,2)

S = 3×1
11.0303
9.4692
5.3229

5、数组页面的标准差

创建一个三维数组并计算每页数据（行和列）的标准差。

A(:,:,1) = [2 4; -2 1];
A(:,:,2) = [9 13; -5 7];
A(:,:,3) = [4 4; 8 -3];
S = std(A,0,[1 2])

S =
S(:,:,1) =
2.5000
S(:,:,2) =
7.7460
S(:,:,3) =
4.5735

6、标准差，不包括 NaN

创建一个向量并计算其标准差，不包括 NaN 值。

A = [1.77 -0.005 3.98 -2.95 NaN 0.34 NaN 0.19];
S = std(A,'omitnan')

S = 2.2797