一：Radon变换

Radon变换：是一种用于将图像从空间域转换到投影域的数学工具，其基本思想是将图像中每个点的灰度值投影到一组直线上，然后将这些投影合并在一起形成投影域。Radon变换可以用于多种图像处理任务，包括图像重建、特征提取、图像分割等

（1）Radon变换原理

Radon变换原理：给定一个函数$f(x,y)$，Radon变换将其投影到一组线上，得到一组投影值$p(\theta ,s)$。其中$\theta$表示投影线的角度，$s$表示投影线与原点的距离。具体而言，对于每个角度$\theta$，Radon变换将在直线$l_{\theta ,s}$上对函数$f(x,y)$进行积分，其中$l_{\theta ,s}$是距离原点为$s$，与$x$轴成$\theta$角度的直线。投影值$p(\theta ,s)$即为积分结果

可以将Radon变换看作是从二维函数到一维函数的映射，其中每个投影值$p(\theta ,s)$表示了投影线$l_{\theta ,s}$上的一维信息。因此，Radon变换可以用于从一组投影值中重建原始函数$f(x,y)$。这种逆变换被称为逆Radon变换或反投影

（2）Radon变换实现

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• [R,xp]=radon(I,theta)：Radon变换是一种用于图像处理中的特征提取的方法，可以用于检测图像中的直线特征
  • I为输入的图像
  • theta为变换角度
  • R为变换后的结果
  • xp为变换后的坐标

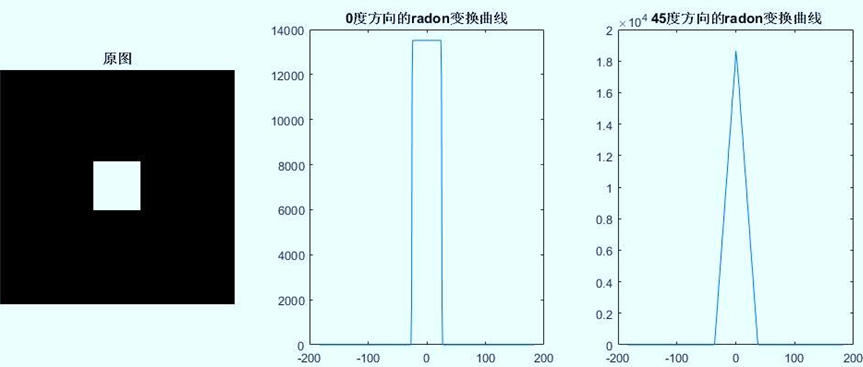
程序1：对图像进行指定方向上的Radon变换

• 首先，代码读取名为’block.bmp’的灰度图像，并将其分别进行0度和45度方向的Radon变换
• 然后，使用subplot函数将原图像和两个变换后的图像显示在同一张图中，方便比较
• 最后，代码展示了两个变换后的图像的Radon变换曲线，分别对应0度和45度方向。这些曲线可以用于检测图像中的直线特征

clear,clc,close all;
Image=rgb2gray(imread('block.bmp'));
[R1,X1]=radon(Image,0);
[R2,X2]=radon(Image,45);
subplot(131),imshow(Image),title('原图');
subplot(132),plot(X1,R1),title('0度方向的radon变换曲线');
subplot(133),plot(X2,R2),title('45度方向的radon变换曲线');

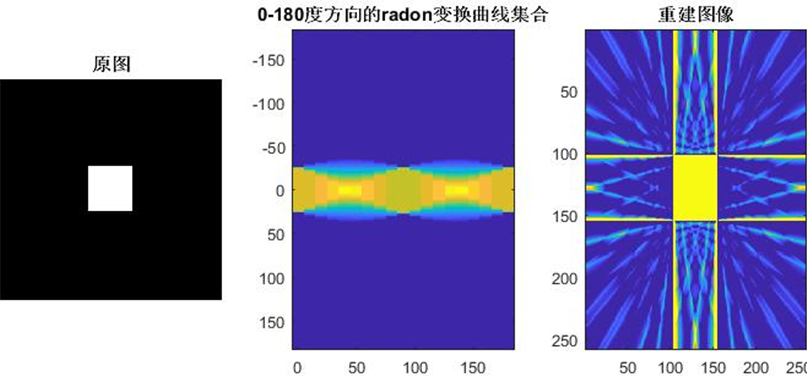
程序2：对图像进行Radon变换和反变换

• 首先，它读取了名为 “block.bmp” 的图像，并将其转换为灰度图像
• 然后，它使用 “radon” 函数计算了图像在 0 到 180 度方向上的 Radon 变换曲线集合，并找到了这些曲线集合中的最大值
• 接着，它使用 “iradon” 函数对这些曲线进行反变换，从而重建出原始图像
• 最后，它使用 “subplot” 函数将原始图像、Radon 变换曲线集合和重建图像显示在同一张图上

clear,clc,close all;
Image=rgb2gray(imread('block.bmp'));
theta=0:10:180;
[R,X]=radon(Image,theta);
C=max(R);
result=iradon(R,theta);
subplot(131),imshow(Image),title('原图');
subplot(132),imagesc(theta,X,R),title('0-180度方向的radon变换曲线集合');
subplot(133),image(result),title('重建图像');

Python实现：使用Python实现上述同样的功能

程序1：对图像进行指定方向上的Radon变换

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# Load the image
Image = cv2.imread('block.bmp', cv2.IMREAD_GRAYSCALE)

# Perform Radon transform
theta = np.arange(0, 180, 1)
R = cv2.radon(Image, theta)

# Display the results
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(10, 5))
ax1.imshow(Image, cmap='gray')
ax1.set_title('Original Image')
ax2.plot(R[:, 0])
ax2.set_title('Radon Transform (0 degrees)')
ax3.plot(R[:, 45])
ax3.set_title('Radon Transform (45 degrees)')
plt.show()

程序2：对图像进行Radon变换和反变换

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']

# Load the image
Image = cv2.imread('block.bmp', cv2.IMREAD_GRAYSCALE)

# Perform Radon transform
theta = np.arange(0, 181, 10)
R = cv2.radon(Image, theta)

# Get the maximum value of the Radon transform
C = np.max(R)

# Perform inverse Radon transform
result = cv2.remap(R, theta, None, cv2.INTER_LINEAR)

# Display the images using matplotlib
fig, axs = plt.subplots(1, 3, figsize=(10, 10))
axs[0].imshow(Image, cmap='gray')
axs[0].set_title('Original Image')
axs[1].imshow(R, cmap='gray', extent=(0, 180, 0, R.shape[0]), aspect='auto')
axs[1].set_title('Radon Transform')
axs[2].imshow(result, cmap='gray')
axs[2].set_title('Reconstructed Image')
plt.show()

（3）Radon变换性质

线性：Radon变换是线性的。即，对于任意常数$a,b$和函数$f,g$，有以下等式成立

R { a f + b g } = a R { f } + b R { g } \mathcal{R}\{a f+b g\}=a \mathcal{R}\{f\}+b \mathcal{R}\{g\} R{af+bg}=aR{f}+bR{g}

其中$\mathcal{R}\cdot$表示Radon变换。这个性质意味着可以通过对原始函数进行线性组合来计算其Radon变换

平移性：Radon变换是平移不变的。即，对于函数$f(x,y)$和距离向量$d=(d_x,d_y)$，有以下等式成立

R { f ( x − d x , y − d y ) } ( θ , s ) = R { f ( x , y ) } ( θ , s − d x cos ⁡ θ − d y sin ⁡ θ ) \mathcal{R}\left\{f\left(x-d_{x}, y-d_{y}\right)\right\}(\theta, s)=\mathcal{R}\{f(x, y)\}\left(\theta, s-d_{x} \cos \theta-d_{y} \sin \theta\right) R{f(x−dx​,y−dy​)}(θ,s)=R{f(x,y)}(θ,s−dx​cosθ−dy​sinθ)

这个性质意味着可以通过平移原始函数来计算其在不同位置上的Radon变换

相似性：Radon变换是相似变换不变的。即，对于函数$f(x,y)$和比例因子$a$，有以下等式成立

R { f ( a x , a y ) } ( θ , s ) = 1 ∣ a ∣ R { f ( x , y ) } ( θ , s ∣ a ∣ ) \mathcal{R}\{f(a x, a y)\}(\theta, s)=\frac{1}{|a|} \mathcal{R}\{f(x, y)\}\left(\theta, \frac{s}{|a|}\right) R{f(ax,ay)}(θ,s)=∣a∣1​R{f(x,y)}(θ,∣a∣s​)

微分：Radon变换具有微分性质。即，对于函数$f(x,y)$，有以下等式成立

∂ ∂ s R { f ( x , y ) } ( θ , s ) = − ∫ − ∞ ∞ ∂ ∂ y f ( x , y ) cos ⁡ θ − ∂ ∂ x f ( x , y ) sin ⁡ θ d x \frac{\partial}{\partial s} \mathcal{R}\{f(x, y)\}(\theta, s)=-\int_{-\infty}^{\infty} \frac{\partial}{\partial y} f(x, y) \cos \theta-\frac{\partial}{\partial x} f(x, y) \sin \theta d x ∂s∂​R{f(x,y)}(θ,s)=−∫−∞∞​∂y∂​f(x,y)cosθ−∂x∂​f(x,y)sinθdx

这个性质意味着可以通过对Radon变换进行微分来计算原始函数的导数

（4）Radon变换应用

Radon变换应用：

• CT图像重建：计算机断层成像（CT）是一种医学成像技术，通过对人体进行X射线扫描来获取其内部结构的三维图像。CT图像可以通过Radon变换进行重建，将CT扫描的投影数据转换为图像数据。这是由于CT扫描是在不同方向上获取的一系列投影图像，而Radon变换可以将这些投影数据转换为图像数据
• 边缘检测：边缘是图像中最重要的特征之一，因为它们可以提供关于图像中物体的轮廓和形状的信息。Radon变换可以用于检测边缘，因为边缘在投影域中表现出明显的特征。通过检测Radon变换后的图像中的峰值，可以确定原始图像中的边缘位置
• 特征提取：Radon变换还可以用于提取图像中的其他特征，例如纹理和形状。通过计算Radon变换的角度分布函数，可以获得图像中纹理和形状的信息
• 图像分割：图像分割是将图像分成若干个互不重叠的区域的过程。Radon变换可以用于图像分割，因为不同区域的投影数据在投影域中表现出不同的特征。通过分析Radon变换后的图像，可以确定原始图像中不同区域的位置

二：小波变换

小波变换：是一种数学工具，用于将信号分解成不同的频率组件。类似于频谱分析，但小波变换可以捕捉到瞬态信号中的时间和频率信息。简单来说，它可以将信号分成多个不同时间长度和频率范围的子信号，以便更好地理解和处理原始信号

（1）小波

A：定义

小波：小波变换中的“小波”指的是一种基本的函数，可以用于将信号分解成不同的频率组件。这些小波函数具有紧凑的支撑和可变的频率和时间分辨率，使得它们可以在时域和频域之间转换，并能够更好地捕捉信号中的局部特征。数学上，小波是一种能够满足一定条件的局部有限能量函数，通常被定义为具有均值为零的波形函数和尺度函数的线性组合。通过将信号与不同尺度和位置的小波函数进行内积运算，可以得到信号在不同频率上的分解系数，进而实现小波变换。设函数$\psi (t)$满足${\int }_R\psi (t)dt=0$，对其进行平移和伸缩产生函数族：${\psi }_{a,b}(t)=\frac{1}{\sqrt{a}}\psi \left(\frac{t-b}{a}\right),a,b\in R,a\ne 0$，$\psi (t)$称为基小波或母小波，$\alpha$为伸缩因子，$b$为平移因子，${\psi }_{a,b}(t)$为$\psi (t)$生成的连续小波。小波有如下特点

• 紧支撑性： 小波函数在小范围内波动，能量有限，超出一定范围时，波动幅度迅速衰减，具有速降性
• 变化性： 小波函数随尺度因子的变化而变化
• $K$阶消失矩： $\begin{array}{l}{\int }_R{t}^k\Psi (t)dt=0,k=0,1,\cdots ,K-1\end{array}$

B：实例

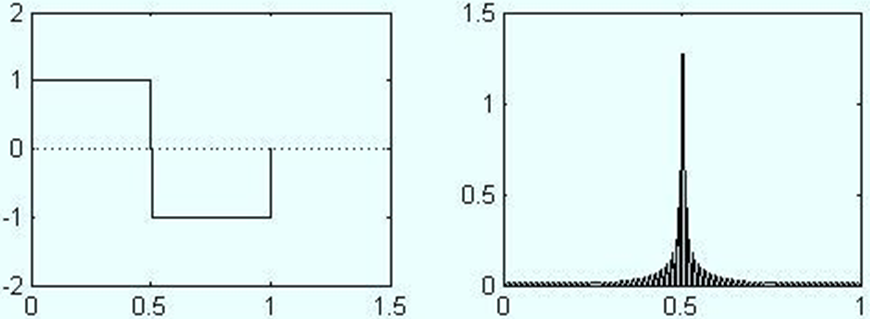
Haar小波：下图为Harr小波及其频谱

$$\{\begin{array}{l}{\Psi }_H(t)=\{\begin{array}{cc}1& 0\le t<1/2\\ -1& 1/2\le t<1\\ 0& \text{ 其他 }\end{array}\\ {\Psi }_H(\omega )=\frac{1-2e^{\frac{i\omega }{2}}+e^{-i\omega }}{\omega i}\end{array}$$

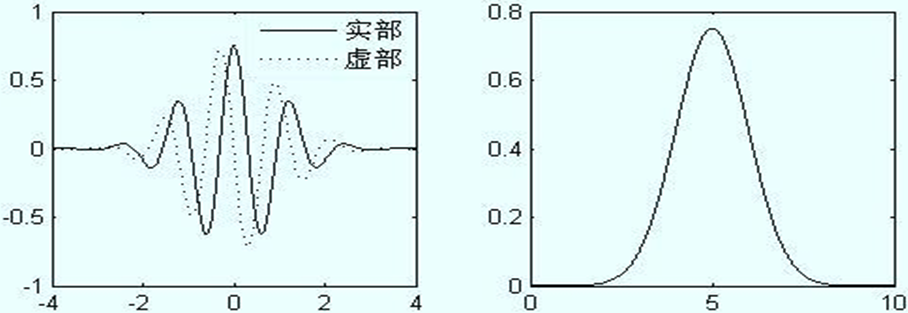
Morlet小波：下图为Morlet小波及其频谱

$$\{\begin{array}{l}\Psi (t)={\pi }^{-1/4}\left(e^{-i{\omega }_{0}t}-e^{-{\omega }_0^2/2}\right)e^{-t^2/2}\\ \Psi (\omega )={\pi }^{-1/4}\left[e^{-{\left(\omega -{\omega }_0\right)}^2/2}-e^{-{\omega }_0^2/2}{e}^{-{\omega }^2/2}\right]\end{array}$$

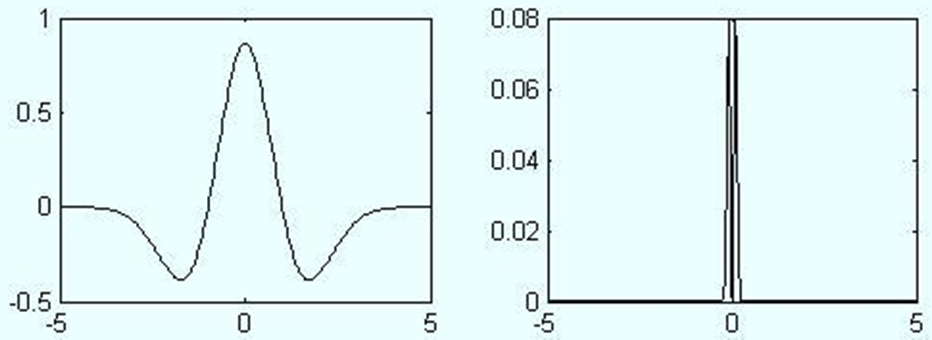
Mexico草帽小波：下图为Mexico草帽小波及其频谱

$$\Psi (t)=\left(\frac{2}{\sqrt{3}}{\pi }^{-1/4}\right)\left(1-t^2\right)e^{-t^2/2}$$

（2）一维小波变换

A：连续小波变换

连续小波变换（Continuous Wavelet Transform，CWT）：给定一个原始信号 $f(t)$，以及一个小波函数 $\psi (t)$，CWT 将 $f(t)$ 与 $\psi (t)$ 进行一系列缩放和平移操作得到一组小波系数 $C_{\psi }(a,b)$，其中 $a$ 和 $b$ 分别表示尺度（缩放因子）和位移（平移因子）。CWT可用如下公式表示

• ${\psi }_{(}t)$ 表示小波函数的复共轭
• ${\psi }^{\ast }(t)$ 表示复共轭操作，即将小波函数 $\psi (t)$ 中的实部变为负数

$$C_{\psi }(a,b)=\frac{1}{\sqrt{a}}{\int }_{-\infty }^{+\infty }f(t){\psi }^{\ast }\left(\frac{t-b}{a}\right)dt$$

CWT 的物理意义是将信号 $f(t)$ 拆分成一系列不同尺度和不同频率的小波，从而可以更好地分析信号的局部特征

B：时频特性

时频特性：是指小波变换能够提供的时间和频率信息。与傅里叶变换只提供频率信息不同，小波变换在时域和频域都提供了有用的信息

• 在时域上小波变换提供了信号的局部时间信息：不同尺度的小波函数可以捕获信号的不同频率成分，而不同位置的小波函数可以捕获信号在不同时间段的局部特征。因此，小波系数可以显示信号的短时特征，并且可以用于分析信号的时域局部特性
• 在频域上小波变换提供了信号的局部频率信息：不同尺度的小波函数可以捕获不同频率范围内的信号成分。在小波系数中，较高频率的小波系数通常与信号的高频成分相关联，而较低频率的小波系数通常与信号的低频成分相关联。因此，小波系数可以用于分析信号的频域局部特性

分析小波${\psi }_{a,b}(t)$时、频窗中心和时，频窗半径，可得

• 时窗中心：$t^{\ast }=a{t}_{\psi }^{\ast }+b$
• 时窗半径：$\Delta t=a\Delta t_{\psi }$
• 频窗中心：$w^{\ast }=\frac{1}{a}{w}_{\psi }^{\ast }$
• 频窗半径：$\Delta w=\frac{1}{a}\Delta w_{\psi }$

$t_{\psi }^{\ast },\Delta t_{\psi },w_{\psi }^{\ast },\Delta w_{\psi }$是基小波$\psi (t)$的时、频窗中心、半径

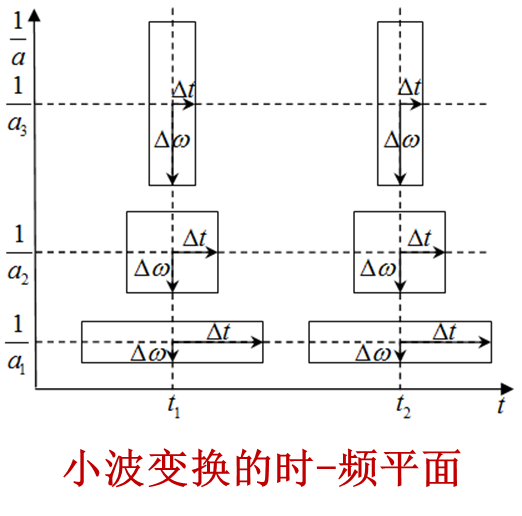
$$2\Delta t\cdot 2\Delta \omega =4a\Delta t_{\psi }\cdot \frac{1}{a}\Delta {\omega }_{\psi }=4\Delta t_{\psi }\cdot \Delta {\omega }_{\psi }$$

对于固定的$b$，当$a>1$时，随着$a$的增大，时窗增宽，频窗变窄，但窗口面积不变

小波变换分析信号具有自适应的时频窗口

• 检测高频分量，尺度参数$a>0$变小，时窗变窄，频窗增高, 主频${\omega }^{\ast }$变大
• 检测低频特性，尺度参数$a>0$增大，时窗变宽，频窗降低, 主频${\omega }^{\ast }$变小

C：离散小波变换

离散小波变换（Discrete Wavelet Transform，DWT）：给定一个长度为 $N$ 的离散信号 $x[n]$，以及一个小波函数 $\psi [n]$，DWT 将 $x[n]$ 与 $\psi [n]$ 进行一系列缩放和平移操作得到一组小波系数 $c_{j,k}$ 和一组近似系数 $d_j$。其中，$j$ 表示尺度（缩放因子），$k$ 表示位移（平移因子）。DWT可以用以下公式表示

• ${\psi }_{j,k}[n]$ 和 ${\varphi }_{j,k}[n]$ 分别表示小波函数和尺度函数的离散缩放和平移版本，可以通过在连续版本中选取适当的尺度和位移进行离散化得到

$$\begin{array}{l}{c}_{j,k}=⟨x[n],{\psi }_{j,k}[n]⟩={\sum }_{n=0}^{N-1}x[n]{\psi }_{j,k}[n]\\ d_j[k]=⟨x[n],{\varphi }_{j,k}[n]⟩={\sum }_{n=0}^{N-1}x[n]{\varphi }_{j,k}[n]\end{array}$$

DWT 的物理意义与 CWT 类似，是将信号 $x[n]$ 拆分成一组不同尺度和不同位置（或频率）的小波系数和近似系数，从而可以更好地分析信号的局部特征。与 CWT 不同的是，DWT 使用离散信号和离散小波函数进行计算，因此可以在计算机上高效地实现

D：正交小波

正交小波（Orthogonal Wavelet Transform，OWT）：给定一个长度为 $N$ 的离散信号 $x[n]$，以及一组正交小波函数 ${\psi }_{j,k}[n],{\varphi }_{j,k}[n]$，OWT 将 $x[n]$ 与小波基进行内积计算，得到一组小波系数 $c_{j,k}$ 和一组近似系数 $d_j$。其中，$j$ 表示尺度（缩放因子），$k$ 表示位移（平移因子）。OWT可用如下公式表示

$$\begin{array}{l}{c}_{j,k}=⟨x[n],{\psi }_{j,k}[n]⟩={\sum }_{n=0}^{N-1}x[n]{\psi }_{j,k}[n]\\ d_j[k]=⟨x[n],{\varphi }_{j,k}[n]⟩={\sum }_{n=0}^{N-1}x[n]{\varphi }_{j,k}[n]\end{array}$$

其中，${\psi }_{j,k}[n]$ 和 ${\varphi }_{j,k}[n]$ 是正交小波函数，满足以下正交条件

• ${\delta }_{i,j}$ $i=j$ 时为 1，否则为 0。这些正交条件保证了正交小波基的正交性和归一性

$$\begin{array}{l}⟨{\psi }_{j,k}[n],{\psi }_{j^{\prime },k^{\prime }}[n]⟩={\delta }_{j,j^{\prime }}{\delta }_{k,k^{\prime }}\\ ⟨{\varphi }_{j,k}[n],{\varphi }_{j^{\prime },k^{\prime }}[n]⟩={\delta }_{j,j^{\prime }}{\delta }_{k,k^{\prime }}\end{array}$$

正交小波基具有多项式性质，可以通过递推算法（如 Daubechies 算法）构造。这种小波基通常比 CWT 和其他小波变换的小波基更容易实现和计算，并且在压缩和信号处理应用中被广泛使用

（3）二维小波变换

A：定义

二维小波变换（Two-Dimensional Wavelet Transform，2DWT）：是一种将二维图像或信号分解为不同尺度和方向上的频率成分的小波变换。它可以将一个 $M\times N$ 的二维信号 $f(x,y)$ 分解为多个尺度和方向上的小波系数 $w_{j,k}(x,y)$ 和近似系数 $a_J(x,y)$，其中 $j$ 表示尺度，$k$ 表示位置，$J$ 是最粗糙的尺度。小波系数和近似系数可以用以下公式计算

$$\begin{array}{l}{w}_{j,k}(x,y)=⟨f(x,y),{\psi }_{j,k}(x,y)⟩={\iint }_{-\infty }^{\infty }f(x,y){\psi }_{j,k}^{\ast }(x,y)dxdy\\ a_J(x,y)=⟨f(x,y),{\varphi }_J(x,y)⟩={\iint }_{-\infty }^{\infty }f(x,y){\varphi }_J^{\ast }(x,y)dxdy\end{array}$$

其中，${\psi }_{j,k}(x,y)$ 和 ${\varphi }_J(x,y)$ 是二维小波基函数，满足正交性和归一化条件：

$$\begin{array}{l}⟨{\psi }_{j,k}(x,y),{\psi }_{j^{\prime },k^{\prime }}(x,y)⟩={\delta }_{j,j^{\prime }}{\delta }_{k,k^{\prime }}\\ ⟨{\varphi }_J(x,y),{\varphi }_J(x,y)⟩=1\end{array}$$

二维小波基函数可以通过将一维小波基函数在两个方向上的张量积得到。可以使用快速小波变换（Fast Wavelet Transform，FWT）等算法对二维小波变换进行计算

二维小逆反变换将小波系数和近似系数重新组合成原始信号 $f(x,y)$，其公式为：

$$f(x,y)=\sum _{j=0}^J\sum _k{w}_{j,k}(x,y)+a_J(x,y)$$

B：图像小波分解

图像小波分解：是将二维图像进行小波变换以得到其不同尺度和方向上的小波系数和近似系数的过程。这种分解提供了一种多分辨率分析图像和识别局部变化的方法。图像小波分解可以使用二维小波变换（如二维离散小波变换或二维冗余小波变换）来实现。通常情况下，二维离散小波变换速度较快且存储需求较小，而二维冗余小波变换则提供了更灵活的表示形式并可以实现更好的压缩性能。图像小波分解包括以下步骤

• 对图像进行二维小波变换，得到每个尺度和方向上的小波系数和近似系数
• 对小波系数进行阈值处理，去除噪声或其他不需要的高频部分。可以使用各种阈值方法，如硬阈值、软阈值或自适应阈值
• 使用小波系数和近似系数重构图像

C：程序

MATLAB实现：相关函数如下，具体解释可看MATLAB帮助手册

• p[CA,CH,CV,CD]=dwt2(X,’wname’) 或 [CA,CH,CV,CD]=dwt2(X, Lo_D, Hi_D)：一级二维离散小波变换
• X=idwt2(CA,CH,CV,CD,’wname’) 或X=idwt2(CA,CH,CV,CD, Lo_D, Hi_D)：一级二维离散小波逆变换
• [C,S] = wavedec2(X,N,'wname') 或[C,S] = wavedec2(X,N,Lo_D,Hi_D)：多级二维小波分解
• X = waverec2(C,S,'wname')或X = waverec2(C,S,Lo_R,Hi_R)：多级二维小波重构
• A = appcoef2(C,S,'wname',N)或A = appcoef2(C,S,Lo_R,Hi_R，N)：提取二维小波分解的低频系数
• D = detcoef2(O,C,S,N) 或[H,V,D] = detcoef2('all',C,S,N)：提取二维小波分解的高频系数

①：一级分解及重构

MATLAB：

Image=imread('cameraman.jpg');     
subplot(1,3,1),imshow(Image),title('原图');                  
grayI=rgb2gray(Image);           
[ca1,ch1,cv1,cd1]=dwt2(grayI,'db4');  
DWTI1=[wcodemat(ca1,256),wcodemat(ch1,256);wcodemat(cv1,256),wcodemat(cd1,256)];
subplot(1,3,2),imshow(DWTI1/256),title('一级分解');    
% imwrite(DWTI2/256,'dwt1.jpg');
result=idwt2(ca1,ch1,cv1,cd1,'db4');
subplot(1,3,3),imshow(result,[]),title('一级重构');
% imwrite(result/256,'redwt1.jpg');

Python：

import cv2
import matplotlib.pyplot as plt
import numpy as np
plt.rcParams['font.sans-serif'] = ['SimHei']

# 读入图像
Image = cv2.imread('cameraman.jpg')

# 显示原图
plt.subplot(1, 3, 1)
plt.imshow(cv2.cvtColor(Image, cv2.COLOR_BGR2RGB))
plt.title('原图')

# 灰度化
grayI = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)

# 一级小波分解
coeffs = pywt.dwt2(grayI, 'db4')
ca1, (ch1, cv1, cd1) = coeffs

# 拼接小波系数矩阵
DWTI1 = np.vstack((np.hstack((ca1, ch1)), np.hstack((cv1, cd1))))

# 显示一级分解结果
plt.subplot(1, 3, 2)
plt.imshow(DWTI1 / 256)
plt.title('一级分解')

# 一级小波重构
result = pywt.idwt2(coeffs, 'db4')

# 显示一级重构结果
plt.subplot(1, 3, 3)
plt.imshow(result, cmap='gray')
plt.title('一级重构')

# 显示图像
plt.show()

②：二级分解及重构

MATLAB：

close all,clear,clc;
Image=imread('cameraman.jpg');     
subplot(1,3,1),imshow(Image);                  
grayI=rgb2gray(Image);           
[ca1,ch1,cv1,cd1]=dwt2(grayI,'db4');  
DWTI2=[wcodemat(ca1,256),wcodemat(ch1,256);wcodemat(cv1,256),wcodemat(cd1,256)];
subplot(1,3,2),imshow(DWTI2/256);    
imwrite(DWTI2/256,'dwt1.jpg');
result=idwt2(ca1,ch1,cv1,cd1,'db4');
subplot(1,3,3),imshow(result,[]);

Image=imread('cameraman.jpg');     
grayI=rgb2gray(Image);           
[c,s]=wavedec2(grayI,2,'db4');
ca2=appcoef2(c,s,'db4',2);
[ch2,cv2,cd2] = detcoef2('all',c,s,2);
[ch1,cv1,cd1] = detcoef2('all',c,s,1);
ca1=[wcodemat(ca2,256),wcodemat(ch2,256);wcodemat(cv2,256),wcodemat(cd2,256)];
k=s(2,1)*2-s(3,1);
ch1=padarray(ch1,[k k],1,'pre');
cv1=padarray(cv1,[k k],1,'pre');
cd1=padarray(cd1,[k k],1,'pre');
DWTI2=[ca1,wcodemat(ch1,256);wcodemat(cv1,256),wcodemat(cd1,256)];
subplot(1,2,1),imshow(DWTI2/256),title('二级分解');    
% imwrite(DWTI2/256,'dwt2.jpg');
result= waverec2(c,s,'db4');
subplot(1,2,2),imshow(result,[]),title('二级重构');
% imwrite(result/256,'redwt2.jpg');

import cv2
import matplotlib.pyplot as plt
import numpy as np
import pywt

# 读入图像
Image = cv2.imread('cameraman.jpg')

# 显示原图
plt.subplot(1, 3, 1)
plt.imshow(cv2.cvtColor(Image, cv2.COLOR_BGR2RGB))
plt.title('原图')

# 灰度化
grayI = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)

# 一级小波分解
coeffs1 = pywt.dwt2(grayI, 'db4')
ca1, (ch1, cv1, cd1) = coeffs1

# 拼接小波系数矩阵
DWTI1 = np.vstack((np.hstack((ca1, ch1)), np.hstack((cv1, cd1))))

# 显示一级分解结果
plt.subplot(1, 3, 2)
plt.imshow(DWTI1 / 256)
plt.title('一级分解')

# 保存一级分解结果
cv2.imwrite('dwt1.jpg', DWTI1 / 256)

# 一级小波重构
result1 = pywt.idwt2(coeffs1, 'db4')

# 显示一级重构结果
plt.subplot(1, 3, 3)
plt.imshow(result1, cmap='gray')
plt.title('一级重构')

# 显示图像
plt.show()

# 读入图像
Image = cv2.imread('cameraman.jpg')

# 灰度化
grayI = cv2.cvtColor(Image, cv2.COLOR_BGR2GRAY)

# 二级小波分解
coeffs2 = pywt.wavedec2(grayI, 'db4', level=2)
ca2 = coeffs2[0]
ch2, cv2, cd2 = coeffs2[1:]

# 一级小波分解
coeffs1 = pywt.wavedec2(grayI, 'db4', level=1)
ch1, cv1, cd1 = coeffs1[1:]

# 根据系数大小调整子带尺寸
k = coeffs2[2][0] * 2 - coeffs2[3][0]
ch1 = np.pad(ch1, ((k, 0), (k, 0)), mode='constant', constant_values=1)
cv1 = np.pad(cv1, ((k, 0), (k, 0)), mode='constant', constant_values=1)
cd1 = np.pad(cd1, ((k, 0), (k, 0)), mode='constant', constant_values=1)

# 拼接小波系数矩阵
ca1 = np.vstack((np.hstack((ca2, ch2)), np.hstack((cv2, cd2))))
DWTI2 = np.vstack((np.hstack((ca1, ch1)), np.hstack((cv1, cd1))))

# 显示二级分解结果
plt.subplot(1, 2, 1)
plt.imshow(DWTI2 / 256)
plt.title('二级分解')

# 二级小波重构
result2 = pywt.waverec2(coeffs2, 'db4')

# 显示二级重构结果
plt.subplot(1, 2, 2)
plt.imshow(result2, cmap='gray')
plt.title

（4）小波变换在图像处理中的应用

小波变换在图像处理中的应用：

• 滤波和噪声去除：小波变换可以将信号分解为不同尺度的频率成分，因此可以通过选择不同的小波基函数来对图像进行频域滤波。此外，小波变换还可以将噪声与信号分离，因此可以使用小波域的软或硬阈值来去除噪声
• 边缘检测：由于小波变换可以提供不同尺度和方向的频率信息，因此可以通过检测小波系数的变化来实现边缘检测。例如，可以通过选择具有高方向选择性的小波基函数来增强边缘信息
• 压缩编码：小波变换可以将信号分解为多个子带，其中一些子带可能具有较低的能量。因此，在压缩编码中，可以选择丢弃这些低能量子带，从而实现压缩编码。此外，小波变换还可以将图像分解为不同分辨率的子带，从而可以根据需要选择不同的分辨率子带来进行编码
• 图像增强：小波变换可以通过增加或减少小波系数来实现图像增强。例如，可以通过增加高频小波系数的值来增强图像的细节，或者通过减少低频小波系数的值来降低图像的模糊度
• 图像融合：小波变换可以将多个图像分解为不同的频率子带，因此可以将来自不同图像的不同子带进行融合。例如，可以将两个具有不同频率特征的图像的高频子带进行融合，以实现更好的细节保留