排序算法相关总结，涉及的排序算法有：插入排序、冒泡排序、选择排序、希尔排序、堆排序、快速排序、归并排序（动图不是自己画的🌞）。

---

稳定性概念:
假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的,否则称为不稳定的。

---

1.插入排序

思路：当前元素左边为有序序列，右边为待排序序列，当前元素与有序数列的最后一个元素依次比较，如果比它大，则不动，若比它小，则有序序列最后一个元素后移一位，为当前元素空出一个坑位，循环比较，直到找到当前元素的位置。

图示：

代码：时间复杂度O(n^2)，空间复杂度O(1)

//插入排序

public class InsertSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10};
        insertSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    //插入排序
    public static void insertSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            //有序区间为 [0,i)
            int k = i;
            //记录i下标当前值 与有序序列比较
            int tmp = arr[i];
            //如果下标合法且比tmp大 则元素后移
            while (k > 0 && tmp < arr[k - 1]) {
                arr[k] = arr[k - 1];
                k--;
            }
            arr[k] = tmp;
        }
    }

2.冒泡排序

冒泡！！！好的解释完了

图示：

代码： 老老老朋友了，时间复杂度O(n^2)，空间复杂度O(1)

//冒泡排序

public class BubbleSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10};
        bubblesort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    //冒泡排序
    public static void bubblesort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            //判断该趟是否发生交换
            boolean flag = true;
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    //交换
                    int tmp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = tmp;
                    flag = false;
                }
            }
            //如果没有发生交换 则说明后面的已经有序 结束循环
            if (flag) {
                break;
            }
        }
    }

3.选择排序

思路：每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

图示：

代码： 时间复杂度O(n^2)，空间复杂度O(1)

//选择排序（将找到的较大元素放置末尾 和上图演示的反着的 但不影响理解）

public class SelectSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10};
        selectSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int maxIdx = 0;
            for (int j = 1; j < arr.length - i; j++) {
                if (arr[j] > arr[maxIdx]) {
                    maxIdx = j;
                }
            }
            //swap
            int idx = arr.length - 1 - i;
            int tmp = arr[maxIdx];
            arr[maxIdx] = arr[idx];
            arr[idx] = tmp;
        }
    }

4.希尔排序

我们知道插入排序元素越有序效率越高，当全部有序时，效率达到O(n)，希尔排序正是利用这个特点，进行了大量的分组插入排序，从而达到有序目的。
基本思想是：先选定一个整数，把待排序文件中所有记录分成个组，所有距离为的记录分在同一组内，并对每一组内的记录进行排序。然后取重复上述分组和排序的工作。当到达=1时，所有记录在统一组内排好序。

图示：

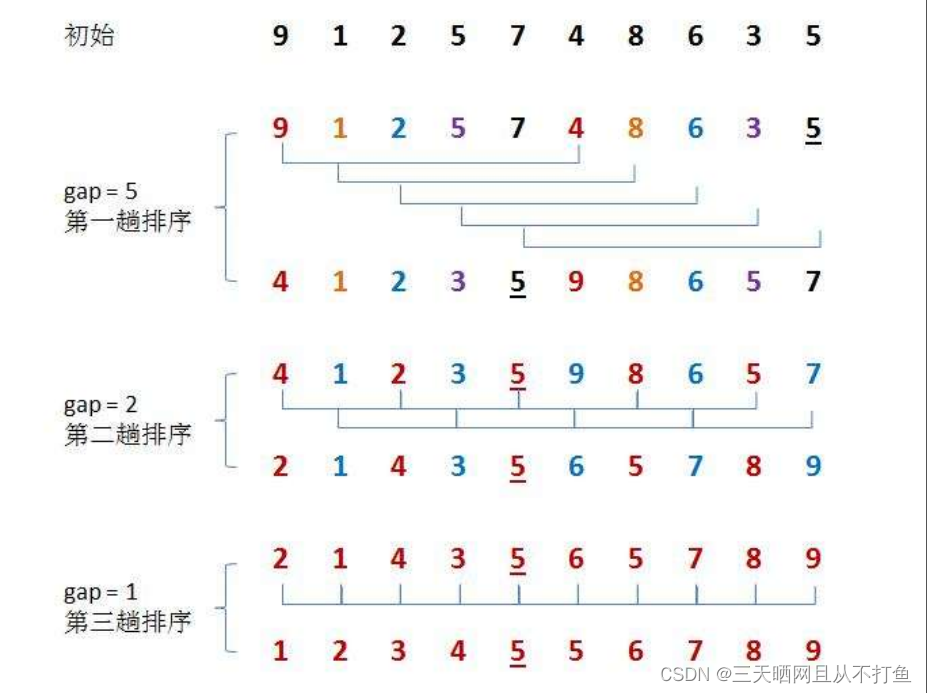
动图：

代码： 时间复杂度O(n^2)，空间复杂度O(1)

//希尔排序

public class ShellSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10, -5, 50, 33, 41, 7, 30, 45, 11};
        shellSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    public static void shellSort(int[] arr) {
        if (arr.length == 0 || arr.length == 1) {
            return;
        }
        int gap = arr.length / 2;
        while (true) {
            for (int i = gap; i < arr.length; i++) {
                int tmp = arr[i];
                int k = i;
                while (k - gap >= 0 && tmp < arr[k - gap]) {
                    arr[k] = arr[k - gap];
                    k -= gap;
                }
                arr[k] = tmp;
            }
            if (gap == 1) {
                break;
            }
            gap /= 2;
        }
    }

5.堆排序

堆排序(Heapsort)是指利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。它是通过堆来进行选择数据。

图示：

代码： 时间复杂度O(N*log(N))，空间复杂度O(1)

//堆排序

public class HeapSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10, -5, 50, 33, 41, 7, 30, 45, 11};
        heapSort(arr);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    public static void heapSort(int[] arr) {
        //建堆
        createHeap(arr);
        for (int i = 0; i < arr.length - 1; i++) {
            swap(arr, 0, arr.length - 1 - i);
            adjustDown(arr, 0, arr.length - 1 - i);
        }
    }

    public static void createHeap(int[] arr) {
        for (int i = (arr.length - 1 - 1) / 2; i >= 0; i--) {
            adjustDown(arr, i, arr.length);
        }
    }

    //在无序区间内进行向下调整
    public static void adjustDown(int[] arr, int idx, int len) {
        while (2 * idx + 1 < len) {
            int maxIdx = 2 * idx + 1;
            int rightIdx = maxIdx + 1;
            if (rightIdx < len && arr[maxIdx] < arr[rightIdx]) {
                maxIdx = rightIdx;
            }
            if (arr[maxIdx] < arr[idx]) {
                break;
            }
            swap(arr, maxIdx, idx);
            //更新
            idx = maxIdx;
        }
    }

    private static void swap(int[] arr, int i, int j) {
        //swap
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

6.快速排序

基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

代码：时间复杂度O(n*logn)，空间复杂度O(log n) ~ O(n)

    public static void quickSort(int[] arr, int from, int to) {
        //判断是否结束
        if (to - from < 1) {
            return;
        }
        //划分方法 下面有实现
        int div = partition(arr, from, to);
        quickSort(arr, from, div - 1);
        quickSort(arr, div + 1, to);
    }

将区间按照基准值划分为左右两半部分的常见方式有：

1.Hoare：

1.选出一个基准值pivot，一般是最左边或最右边的为基准值
2.找到右边第一个小于pivot的值
3.找到左边第一个大于pivot的值
4.交换两个值，然后重复步骤2、3
5.将基准值放到i == j 的位置，返回基准值下标

    public static int partition(int[] arr, int left, int right) {
        int i = left;
        int j = right;
        int pivot = arr[left];
        while (i < j) {
            //注意这里判断j与先判断i的区别
            //先判断j：当i == j时 arr[i] == arr[j] <= povit
            //先判断i：当i == j时 arr[i] == arr[j] >= povit
            while (i < j && arr[j] >= povit) {
                j--;
            }
            while (i < j && arr[i] <= povit) {
                i++;
            }
            swap(arr, i, j);
        }
        swap(arr, left, i);
        return i;
    }

图示：

2.挖坑法：

1.选出一个基准值pivot，一般是最左边或最右边的为基准值 让它做坑位
2.找到右边第一个小于pivot的值 将该值放入坑位 该值的原下标做为新坑位
3.找到左边第一个大于pivot的值 将该值放入坑位 该值的原下标做为新坑位
4.重复步骤2、3
5.将基准值放到i == j 的位置，返回基准值下标

    public static int partition(int[] arr, int left, int right) {
        int i = left;
        int j = right;
        int pivot = arr[left];
        while (i < j) {
            while (i < j && arr[j] >= pivot) {
                j--;
            }
            arr[i] = arr[j];
            while (i < j && arr[i] <= pivot) {
                i++;
            }
            arr[j] = arr[i];
        }
        arr[i] = pivot;
        return i;
    }

图示：

3.前后指针法：

1.选出一个基准值pivot，一般是最左边或最右边的为基准值
2.规定[0,pre)为小于pivot的范围，[pre,right]为大于pivot的范围
3.遍历找小于pivot的值，交换arr[pre]和该值，然后pre++
4.最后将pivot值放入数组，放哪里合适呢？当然是pre - 1处，这样确保它的右边大于等于pivot，左边小于等于pivot

    public static int partition(int[] arr, int left, int right) {
        int pre = left + 1;
        int pivot = arr[left];
        for (int cur = pre; cur <= right; cur++) {
            if (arr[cur] < pivot) {
                swap(arr, cur, pre);
                pre++;
            }
        }
        swap(arr, pre - 1, left);
        return pre - 1;
    }

7.归并排序

基本思想：归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

图示：

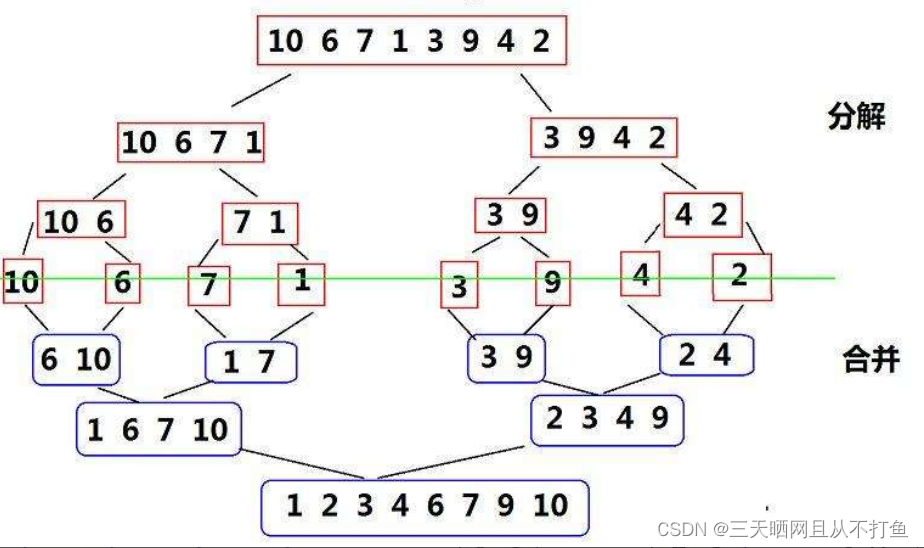
动图：

代码：时间复杂度O(n*logn)，空间复杂度O(n)

//归并排序

public class MergeSort {
    public static void main(String[] args) {
        //验证
        int[] arr = new int[]{5, 4, 3, 8, 4, 1, 6, 0, 9, 10, -5, 50, 33, 41, 7, 30, 45, 11};
        mergeSort(arr, 0, arr.length);
        for (int i : arr) {
            System.out.print(i + " ");
        }
    }

    //[)
    public static void mergeSort(int[] arr, int start, int end) {
        if (end - start <= 1) {
            return;
        }
        int mid = start + (end - start) / 2;

        mergeSort(arr, start, mid);
        mergeSort(arr, mid, end);

        merge(arr, start, mid, end);
    }

    public static void merge(int[] arr, int start, int mid, int end) {
        int[] e = new int[end - start];
        int eIdx = 0;
        int leftIdx = start;
        int rightIdx = mid;
        //归并
        while (leftIdx < mid || rightIdx < end) {
            if (leftIdx == mid) {
                e[eIdx++] = arr[rightIdx++];
            } else if (rightIdx == end) {
                e[eIdx++] = arr[leftIdx++];
            } else if (arr[leftIdx] <= arr[rightIdx]) {
                e[eIdx++] = arr[leftIdx++];
            } else {
                e[eIdx++] = arr[rightIdx++];
            }
        }
        //放回原数组
        for (int i = 0; i < e.length; i++) {
            arr[start + i] = e[i];
        }
    }
}

总结

排序算法	时间复杂度（平均）	时间复杂度（最坏）	时间复杂度（最好）	空间复杂度	稳定性
插入排序	O(n^2)	O(n^2)	O(n)	O(1)	稳定
冒泡排序	O(n^2)	O(n^2)	O(n)	O(1)	稳定
选择排序	O(n^2)	O(n^2)	O(n^2)	O(1)	不稳定
希尔排序	O(n^1.3)	O(n^2)	O(n)	O(1)	不稳定
堆排序	O(n*log n)	O(n*log n)	O(n*log n)	O(1)	不稳定
快速排序	O(n*log n)	O(n^2)	O(n*log n)	O(log n) ~ O(n)	不稳定
归并排序	O(n*log n)	O(n*log n)	O(n*log n)	O(n)	稳定