逻辑回归：是用来进行分类的。

逻辑回归的线性预测输出可以写成：y^=wTx+b

引入Sigmoid函数，让输出限定在[0,1]之间，y^=Sigmoid(wTx+b)=σ(wTx+b)

单个样本损失函数：L(y^,y)=−(ylog y^+(1−y)log (1−y^))

对逻辑回归进行梯度计算。对单个样本而言，逻辑回归Loss function表达式如下：

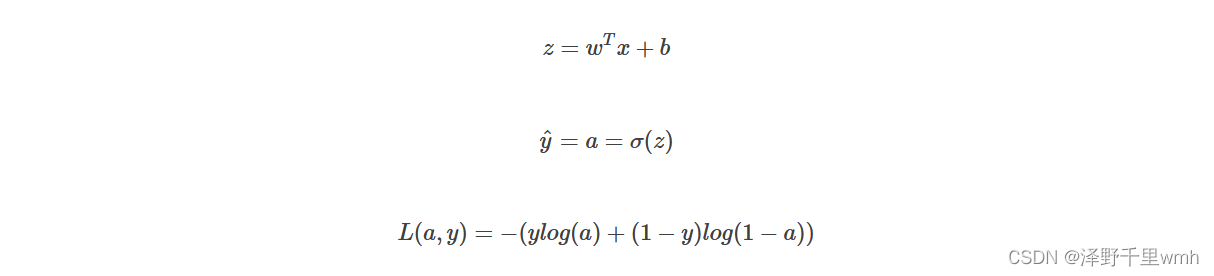
 首先，该逻辑回归的正向传播过程非常简单。根据上述公式，例如输入样本x有两个特征，相应的权重w维度也是2，即。则，最后的Loss function如下所示：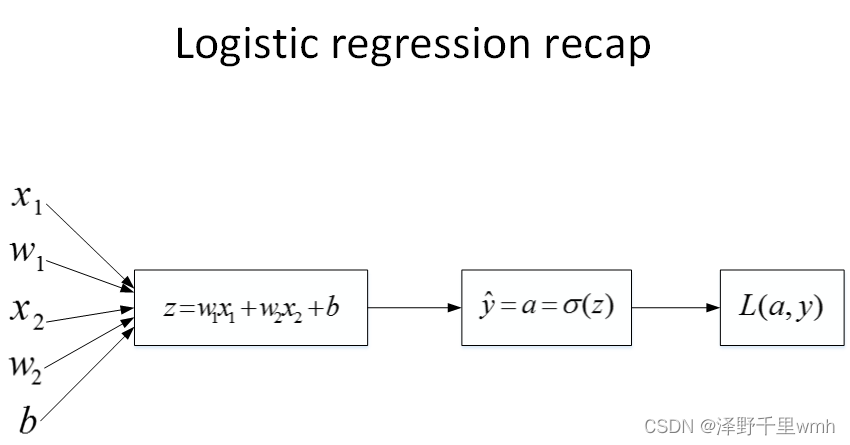

然后，计算该逻辑回归的反向传播过程，即由Loss function计算参数w和b的偏导数。推导过程如下：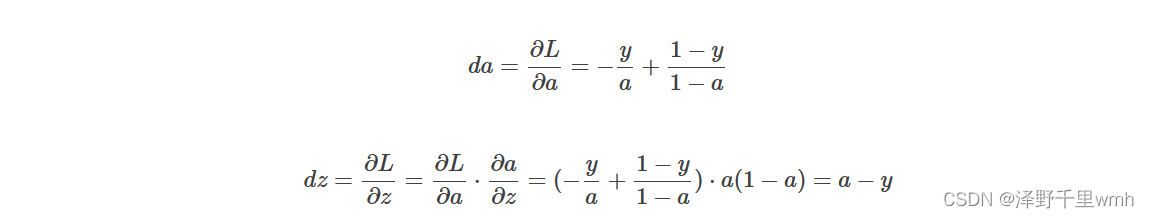 

知道了dz之后，就可以直接对，和b进行求导了。 

 

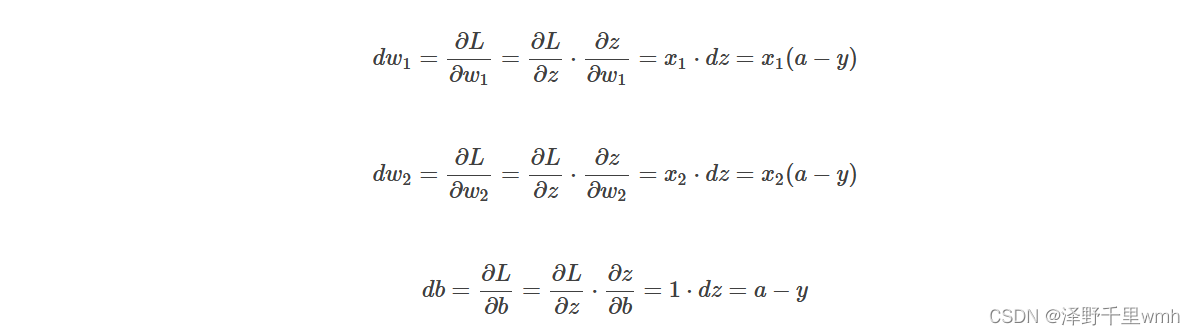
则梯度下降算法可表示为：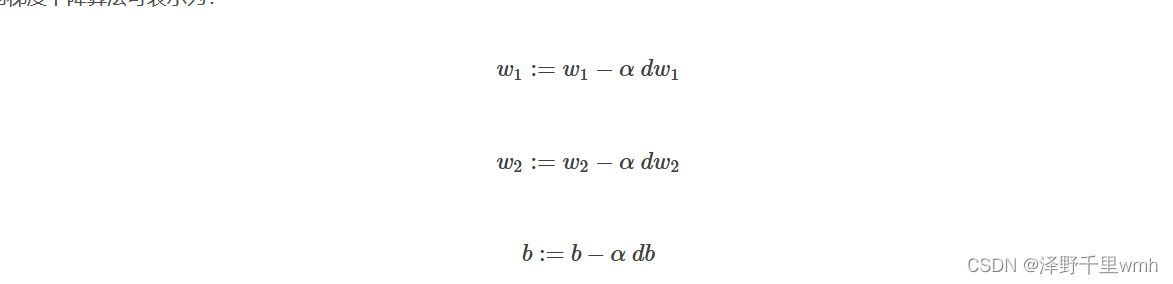 

 

 

 

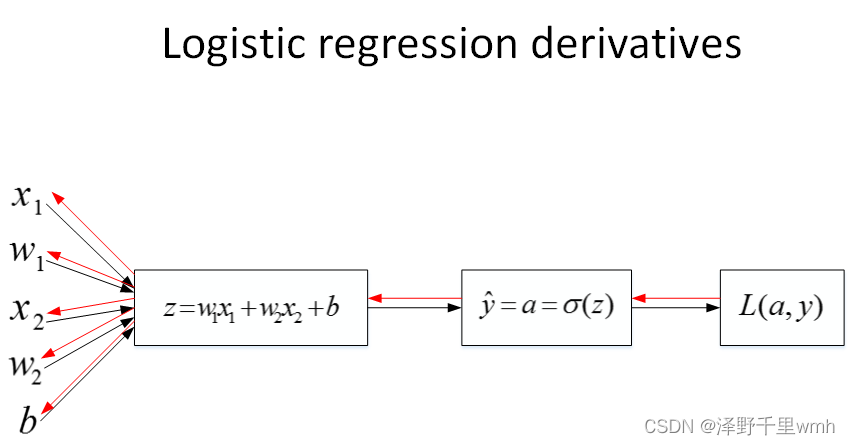
计算该逻辑回归的反向传播过程，即由Loss function计算参数w和b的偏导数

dj/da的偏导数越大，则变量a对结果j的影响就越大