LeetCode算法小抄--归并排序详解及应用
- 归并排序详解及应用
- [912. 排序数组](https://leetcode.cn/problems/sort-an-array/)
- [315. 计算右侧小于当前元素的个数](https://leetcode.cn/problems/count-of-smaller-numbers-after-self/)[hard]--华为笔试
- [493. 翻转对](https://leetcode.cn/problems/reverse-pairs/)[hard]
- [327. 区间和的个数](https://leetcode.cn/problems/count-of-range-sum/)[hard]
⚠申明: 未经许可,禁止以任何形式转载,若要引用,请标注链接地址。 全文共计9208字,阅读大概需要5分钟
🌈更多学习内容, 欢迎👏关注👀【文末】我的个人微信公众号:不懂开发的程序猿
个人网站:https://jerry-jy.co/
归并排序详解及应用
归并排序的代码框架
// 定义:排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = (lo + hi) / 2;
// 利用定义,排序 nums[lo..mid]
sort(nums, lo, mid);
// 利用定义,排序 nums[mid+1..hi]
sort(nums, mid + 1, hi);
/****** 后序位置 ******/
// 此时两部分子数组已经被排好序
// 合并两个有序数组,使 nums[lo..hi] 有序
merge(nums, lo, mid, hi);
/*********************/
}
// 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
// 合并为有序数组 nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);
总结归并排序:先把左半边数组排好序,再把右半边数组排好序,然后把两半数组合并。
类似于二叉树的后序遍历:先递归左子树,再递归右子树,然后写后序位置
归并排序的过程可以在逻辑上抽象成一棵二叉树,树上的每个节点的值可以认为是 nums[lo..hi],叶子节点的值就是数组中的单个元素
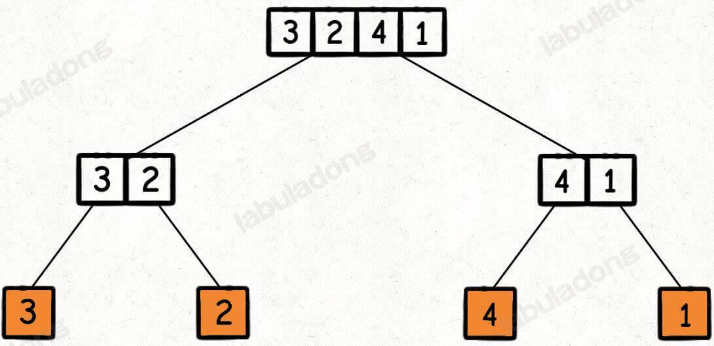
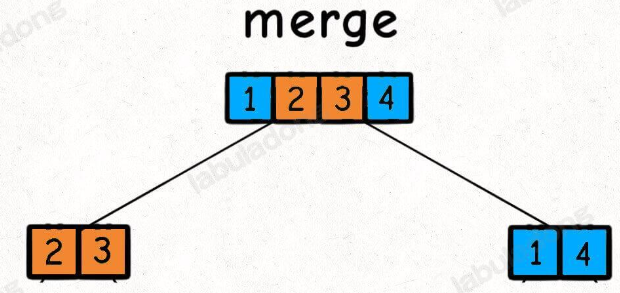
然后,在每个节点的后序位置(左右子节点已经被排好序)的时候执行 merge 函数,合并两个子节点上的子数组
class Merge {
// 用于辅助合并有序数组
private static int[] temp;
public static void sort(int[] nums) {
// 先给辅助数组开辟内存空间
temp = new int[nums.length];
// 排序整个数组(原地修改)
sort(nums, 0, nums.length - 1);
}
// 定义:将子数组 nums[lo..hi] 进行排序
private static void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
// 单个元素不用排序
return;
}
// 这样写是为了防止溢出,效果等同于 (hi + lo) / 2
int mid = lo + (hi - lo) / 2;
// 先对左半部分数组 nums[lo..mid] 排序
sort(nums, lo, mid);
// 再对右半部分数组 nums[mid+1..hi] 排序
sort(nums, mid + 1, hi);
// 将两部分有序数组合并成一个有序数组
merge(nums, lo, mid, hi);
}
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
private static void merge(int[] nums, int lo, int mid, int hi) {
// 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
// 左半边数组已全部被合并
nums[p] = temp[j++];
} else if (j == hi + 1) {
// 右半边数组已全部被合并
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
注意我们不是在 merge 函数执行的时候 new 辅助数组,而是提前把 temp 辅助数组 new 出来了,这样就避免了在递归中频繁分配和释放内存可能产生的性能问题
归并排序的时间复杂度, O(NlogN)
递归算法的复杂度计算,就是子问题个数 x 解决一个子问题的复杂度
执行的次数是二叉树节点的个数,每次执行的复杂度就是每个节点代表的子数组的长度,所以总的时间复杂度就是整棵树中「数组元素」的个数。
所以从整体上看,这个二叉树的高度是 logN,其中每一层的元素个数就是原数组的长度 N,所以总的时间复杂度就是 O(NlogN)。
912. 排序数组
给你一个整数数组 nums,请你将该数组升序排列。
// class Solution {
// public int[] sortArray(int[] nums) {
// // API选手(手动狗头)
// Arrays.sort(nums);
// return nums;
// }
// }
// 归并排序
class Solution {
public int[] sortArray(int[] nums) {
Merge.sort(nums);
return nums;
}
}
class Merge {
// 用于辅助合并有序数组
private static int[] temp;
public static void sort(int[] nums) {
// 先给辅助数组开辟内存空间
temp = new int[nums.length];
// 排序整个数组(原地修改)
sort(nums, 0, nums.length - 1);
}
// 定义:将子数组 nums[lo..hi] 进行排序
private static void sort(int[] nums, int lo, int hi) {
if (lo == hi) {
// 单个元素不用排序
return;
}
// 这样写是为了防止溢出,效果等同于 (hi + lo) / 2
int mid = lo + (hi - lo) / 2;
// 先对左半部分数组 nums[lo..mid] 排序
sort(nums, lo, mid);
// 再对右半部分数组 nums[mid+1..hi] 排序
sort(nums, mid + 1, hi);
// 将两部分有序数组合并成一个有序数组
merge(nums, lo, mid, hi);
}
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
private static void merge(int[] nums, int lo, int mid, int hi) {
// 先把 nums[lo..hi] 复制到辅助数组中
// 以便合并后的结果能够直接存入 nums
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
// 左半边数组已全部被合并
nums[p] = temp[j++];
} else if (j == hi + 1) {
// 右半边数组已全部被合并
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
315. 计算右侧小于当前元素的个数[hard]–华为笔试
给你一个整数数组 nums ,按要求返回一个新数组 counts 。数组 counts 有该性质: counts[i] 的值是 nums[i] 右侧小于 nums[i] 的元素的数量。
class Solution {
public List<Integer> countSmaller(int[] nums) {
// 暴力破解
// 超出时间限制
List<Integer> counts = new LinkedList<>();
for(int i = 0; i < nums.length; i++){
int count = 0;
for(int j = i + 1; j < nums.length; j++){
if(nums[j] < nums[i]) count++;
}
counts.add(count);
}
return counts;
}
}
考虑归并排序
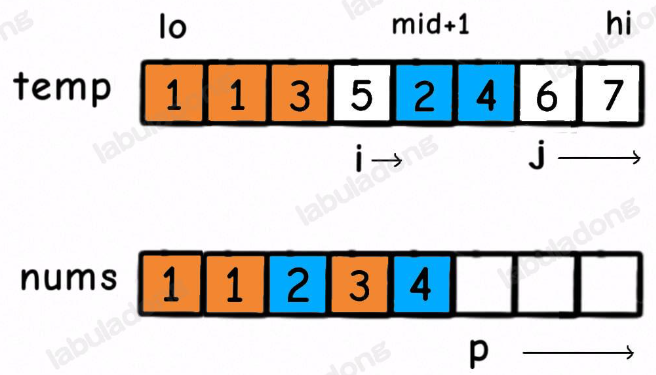
和归并排序什么关系呢,主要在 merge 函数,我们在使用 merge 函数合并两个有序数组的时候,其实是可以知道一个元素 nums[i] 后边有多少个元素比 nums[i] 小的。
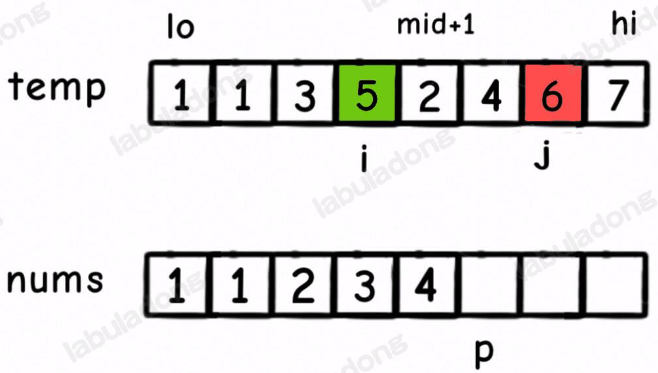
这时候我们应该把 temp[i] 放到 nums[p] 上,因为 temp[i] < temp[j]。
但就在这个场景下,我们还可以知道一个信息:5 后面比 5 小的元素个数就是 左闭右开区间 [mid + 1, j) 中的元素个数,即 2 和 4 这两个元素:
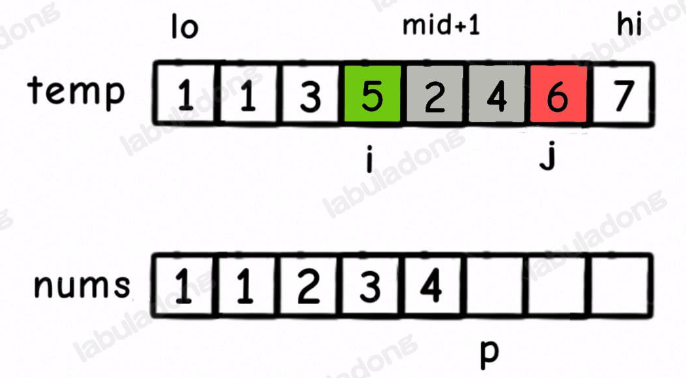
换句话说,在对 nums[lo..hi] 合并的过程中,每当执行 nums[p] = temp[i] 时,就可以确定 temp[i] 这个元素后面比它小的元素个数为 j - mid - 1。
class Solution {
private class Pair {
int val, id;
Pair(int val, int id) {
// 记录数组的元素值
this.val = val;
// 记录元素在数组中的原始索引
this.id = id;
}
}
// 归并排序所用的辅助数组
private Pair[] temp;
// 记录每个元素后面比自己小的元素个数
private int[] count;
public List<Integer> countSmaller(int[] nums) {
int n = nums.length;
count = new int[n];
temp = new Pair[n];
Pair[] arr = new Pair[n];
// 记录元素原始的索引位置,以便在 count 数组中更新结果
for (int i = 0; i < n; i++)
arr[i] = new Pair(nums[i], i);
// 执行归并排序,本题结果被记录在 count 数组中
sort(arr, 0, n - 1);
List<Integer> res = new LinkedList<>();
for (int c : count) res.add(c);
return res;
}
// 归并排序
private void sort(Pair[] arr, int lo, int hi) {
if (lo == hi) return;
int mid = lo + (hi - lo) / 2;
sort(arr, lo, mid);
sort(arr, mid + 1, hi);
merge(arr, lo, mid, hi);
}
// 合并两个有序数组
private void merge(Pair[] arr, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = arr[i];
}
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) { // 左边数组已经排序好了
arr[p] = temp[j++];
} else if (j == hi + 1) { // 右边数组已经排序好了
arr[p] = temp[i++];
// 更新 count 数组
count[arr[p].id] += j - mid - 1;
} else if (temp[i].val > temp[j].val) {
arr[p] = temp[j++];
} else {
arr[p] = temp[i++];
// 更新 count 数组
count[arr[p].id] += j - mid - 1;
}
}
}
}
因为在排序过程中,每个元素的索引位置会不断改变,所以我们用一个 Pair 类封装每个元素及其在原始数组 nums 中的索引,以便 count 数组记录每个元素之后小于它的元素个数。
493. 翻转对[hard]
给定一个数组 nums ,如果 i < j 且 nums[i] > 2*nums[j] 我们就将 (i, j) 称作一个重要翻转对。
你需要返回给定数组中的重要翻转对的数量。
这道题目和题目是一个意思,而且和上一道题非常类似,只不过上一题求的是 nums[i] > nums[j],这里求的是 nums[i] > 2*nums[j] 罢了
解题的思路当然还是要在 merge 函数中做点手脚,当 nums[lo..mid] 和 nums[mid+1..hi] 两个子数组完成排序后,对于 nums[lo..mid] 中的每个元素 nums[i],去 nums[mid+1..hi] 中寻找符合条件的 nums[j] 就行了
// 记录「翻转对」的个数
int count = 0;
// 将 nums[lo..mid] 和 nums[mid+1..hi] 这两个有序数组合并成一个有序数组
private void merge(int[] nums, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 在合并有序数组之前,加点私货
for (int i = lo; i <= mid; i++) {
// 对于左半边的每个 nums[i],都去右半边寻找符合条件的元素
for (int j = mid + 1; j <= hi; j++) {
// nums 中的元素可能较大,乘 2 可能溢出,所以转化成 long
if ((long)nums[i] > (long)nums[j] * 2) {
count++;
}
}
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
nums[p] = temp[j++];
} else if (j == hi + 1) {
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
不过呢,这段代码提交会超时,毕竟额外添加了一个嵌套 for 循环。怎么进行优化呢,注意子数组 nums[lo..mid] 是排好序的,也就是 nums[i] <= nums[i+1]。
所以,对于 nums[i], lo <= i <= mid,我们在找到的符合 nums[i] > 2*nums[j] 的 nums[j], mid+1 <= j <= hi,也必然也符合 nums[i+1] > 2*nums[j]。
换句话说,我们不用每次都傻乎乎地去遍历整个 nums[mid+1..hi],只要维护一个开区间边界 end,维护 nums[mid+1..end-1] 是符合条件的元素即可
class Solution {
public int reversePairs(int[] nums) {
// 执行归并排序
sort(nums);
return count;
}
private int[] temp;
public void sort(int[] nums) {
temp = new int[nums.length];
sort(nums, 0, nums.length - 1);
}
// 归并排序
private void sort(int[] arr, int lo, int hi) {
if (lo == hi) return;
int mid = lo + (hi - lo) / 2;
sort(arr, lo, mid);
sort(arr, mid + 1, hi);
merge(arr, lo, mid, hi);
}
// 记录「翻转对」的个数
private int count = 0;
private void merge(int[] nums, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 进行效率优化,维护左闭右开区间 [mid+1, end) 中的元素乘 2 小于 nums[i]
// 为什么 end 是开区间?因为这样的话可以保证初始区间 [mid+1, mid+1) 是一个空区间
int end = mid + 1;
for (int i = lo; i <= mid; i++) {
// nums 中的元素可能较大,乘 2 可能溢出,所以转化成 long
while (end <= hi && (long)nums[i] > (long)nums[end] * 2) {
end++;
}
count += end - (mid + 1);
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
nums[p] = temp[j++];
} else if (j == hi + 1) {
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
327. 区间和的个数[hard]
给你一个整数数组 nums 以及两个整数 lower 和 upper 。求数组中,值位于范围 [lower, upper] (包含 lower 和 upper)之内的 区间和的个数 。
区间和 S(i, j) 表示在 nums 中,位置从 i 到 j 的元素之和,包含 i 和 j (i ≤ j)。
简单说,题目让你计算元素和落在 [lower, upper] 中的所有子数组的个数。
首先,解决这道题需要快速计算子数组的和,创建一个前缀和数组 preSum 来辅助我们迅速计算区间和。
preSum 中的两个元素之差其实就是区间和。
class Solution {
private int lower, upper;
public int countRangeSum(int[] nums, int lower, int upper) {
this.lower = lower;
this.upper = upper;
// 构建前缀和数组,注意 int 可能溢出,用 long 存储
long[] preSum = new long[nums.length + 1];
for (int i = 0; i < nums.length; i++) {
preSum[i + 1] = (long)nums[i] + preSum[i];
}
// 对前缀和数组进行归并排序
sort(preSum);
return count;
}
private long[] temp;
public void sort(long[] nums) {
temp = new long[nums.length];
sort(nums, 0, nums.length - 1);
}
private void sort(long[] nums, int lo, int hi) {
if (lo == hi) {
return;
}
int mid = lo + (hi - lo) / 2;
sort(nums, lo, mid);
sort(nums, mid + 1, hi);
merge(nums, lo, mid, hi);
}
private int count = 0;
private void merge(long[] nums, int lo, int mid, int hi) {
for (int i = lo; i <= hi; i++) {
temp[i] = nums[i];
}
// 在合并有序数组之前加点私货(这段代码会超时)
// for (int i = lo; i <= mid; i++) {
// for (int j = mid + 1; j <= hi; k++) {
// // 寻找符合条件的 nums[j]
// long delta = nums[j] - nums[i];
// if (delta <= upper && delta >= lower) {
// count++;
// }
// }
// }
// 进行效率优化
// 维护左闭右开区间 [start, end) 中的元素和 nums[i] 的差在 [lower, upper] 中
int start = mid + 1, end = mid + 1;
for (int i = lo; i <= mid; i++) {
// 如果 nums[i] 对应的区间是 [start, end),
// 那么 nums[i+1] 对应的区间一定会整体右移,类似滑动窗口
while (start <= hi && nums[start] - nums[i] < lower) {
start++;
}
while (end <= hi && nums[end] - nums[i] <= upper) {
end++;
}
count += end - start;
}
// 数组双指针技巧,合并两个有序数组
int i = lo, j = mid + 1;
for (int p = lo; p <= hi; p++) {
if (i == mid + 1) {
nums[p] = temp[j++];
} else if (j == hi + 1) {
nums[p] = temp[i++];
} else if (temp[i] > temp[j]) {
nums[p] = temp[j++];
} else {
nums[p] = temp[i++];
}
}
}
}
我们依然在 merge 函数合并有序数组之前加了一些逻辑,这个效率优化有点类似维护一个滑动窗口,让窗口中的元素和 nums[i] 的差落在 [lower, upper] 中。
所有递归的算法,本质上都是在遍历一棵(递归)树,然后在节点(前中后序位置)上执行代码。你要写递归算法,本质上就是要告诉每个节点需要做什么。
–end–




![[网络安全提高篇] 一二〇.恶意软件动态分析经典沙箱Cape批量提取动态API特征](https://img-blog.csdnimg.cn/15bbcc509c7041ea8d2ec84cc1a642c4.png#pic_center)