今天主要介绍DAG (Directed acyclic graph),有向无环图。
无向图的问题相对有向图比较简单,比如岛屿问题,迷宫问题等。
在有向图中,我们通常只关注环是否存在,因为有向图中环的存在会让我们的程序陷入死循环。
举个例子,有向图中的方向通常指代一些事情的执行顺序,比如说[a, b], [b, c]
我们假设a,b,c是三门课程,要学左边的课程之后才能学右边的课程,所以这里我们如果要学c,就要先学a,再学b,最后才能学c。
那如果有环,【a,b】,【b,a】,显然这是矛盾的。
同样。对于一些列复杂的课程
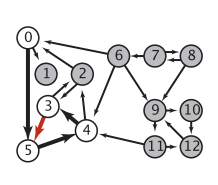
若我们想学5,则要先学3,要学3则要先学4,而要学4则要先学5…这无解
这会让我们DFS的搜索陷入循环。
所以一般我们进行搜索的时候,需要判断环是否存在。
另外我们还要提一下【拓扑排序】
刚刚的课程选择问题中,是一种优先级限制下的调度问题,在有向图中它的定义是
在满足限制条件的情况下如何安排并完成所有任务。
我们可以画出一张有向图,顶点对应任务(通过数组索引来表示课程),有向边对应优先级顺序。
而有向图中的优先级限制下的调度问题,等价于【拓扑排序】,它的定义是:
给定一副有向图,将所有的顶点排序,使得所有的有向边均从排在前面的顶点指向排在后面的顶点。 如下图
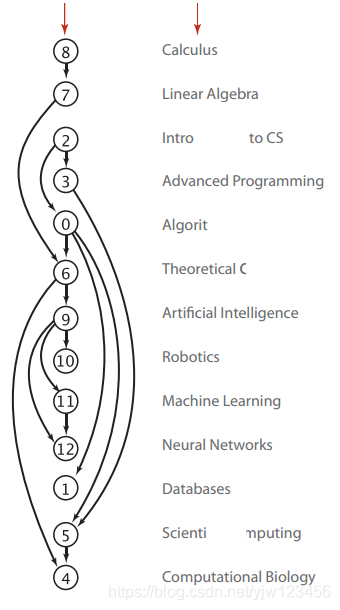
同学可以按照上面排序之后的有向图修完所有课程。
我们利用DFS寻找环:
维护一个递归调用期间已访问的顶点的栈Stack,若(在递归调用期间,通过判断onStack标记数组)两次访问了某个顶点,则说明有环;若DFS递归调用完毕,说明无环。
上面说的还是比较抽象。但是已经大致有一个印象了,就是,有向无环图因为它的顺序限制原因,已经搜索完的点,是不可能再次回到它这里的。
具体的,我们参考上面拓扑排序的图,当搜索到某个点,它没有相邻节点,它就入栈。
所以最终结果是,我们将 最后的课程4放在了栈底,最初的课程8放在栈的最顶部。
由于搜索是从随机的点开始的,我们将没有相邻节点的点入栈之后,再回溯到初始节点,将它入栈,但是后面的搜索也可能会碰到它。所以要给已经搜索的节点打上标签。
另外要注意一点,有些情况下会提示图中无环,但是有些题目不会提示,所以我们考虑一下再搜索过程中判断是否有环,具体的,对于某些节点X,我们搜索过,但是因为我们还没找到那个没有相邻节点的点end,或者我们还没有从end回溯到X,那么此时X节点的状态就是【搜索中】,如果我们搜索的过程中,两次搜索到X,那说明到X节点的图不是单向的,而是存在一个环。
所以,我们将节点分类为【搜索中】【已搜索】【未搜索】
假设有一对相邻节点(u,v),方向是u到 v 。
我们从u开始搜索,此时需要判断v的状态
【v是未搜索】:那我们可以搜索v,搜索完成之后,回溯到u 。
【v是搜索中】:那表示有一个环经过了v节点,这种情况下不存在拓扑排序。
【v是已搜索】:那v已经入栈了,而u不在栈中,那么u入栈就和v没关系,只看u自己的其他相邻节点来决定它的入栈时间即可。
下面用题目演示更直白
LeetCode 210 课程表II
https://leetcode.cn/problems/course-schedule-ii/
现在你总共有 numCourses 门课需要选,记为 0 到 numCourses - 1。
给你一个数组 prerequisites ,其中 prerequisites[i] = [ai, bi] ,
表示在选修课程 ai 前 必须 先选修 bi 。
例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示:[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序,你只要返回 任意一种 就可以了。如果不可能完成所有课程,返回 一个空数组 。
实例1
输入:numCourses = 2, prerequisites = [[1,0]]
输出:[0,1]
解释:总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
实例2
输入:numCourses = 4, prerequisites = [[1,0],[2,0],[3,1],[3,2]]
输出:[0,2,1,3]
解释:总共有 4 门课程。要学习课程 3,你应该先完成课程 1 和课程 2。并且课程 1 和课程 2 都应该排在课程 0 之后。
因此,一个正确的课程顺序是 [0,1,2,3] 。另一个正确的排序是 [0,2,1,3] 。
实例3
输入:numCourses = 1, prerequisites = []
输出:[0]
import collections
class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]) -> List[int]:
edges = collections.defaultdict(list) # 有向图的表达方式
for x in prerequisites:
edges[x[1]].append(x[0]) # 每个点 和 它能到的相邻节点
has_circle = False #是否包含环
res = [] # 栈底是没有相邻节点的点,栈顶是源点,返回res[::-1]
state = [0]*numCourses# 0 1 2 代表未搜索 搜索中,已搜索
def dfs(current):
nonlocal has_circle # nonlocal:函数之外定义,函数之内改变值
state[current]=1
for v in edges[current]:
if state[v] ==1:
has_circle=True
return
elif state[v] ==0:
dfs(v)
if has_circle:
return
else:
continue
state[current]=2 # 每次的dfs会添加一个节点到栈底,这个节点没有指向任何节点
res.append(current)
for i in range(numCourses):
if not has_circle and not state[i]:
dfs(i)
if has_circle:
return []
return res[::-1]
LeetCode 207 课程表
https://leetcode.cn/problems/course-schedule/
你这个学期必须选修 numCourses 门课程,记为 0 到 numCourses - 1 。
在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出,其中 prerequisites[i] = [ai, bi] ,表示如果要学习课程 ai 则 必须 先学习课程 bi 。
例如,先修课程对 [0, 1] 表示:想要学习课程 0 ,你需要先完成课程 1 。
请你判断是否可能完成所有课程的学习?如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
解答方法就是判断这个有向图中有没有环。比上一题更简单。
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]) -> bool:
# 不能完成的几个情况
# 图中有环,自相矛盾
import collections
edges = collections.defaultdict(list)
for x in prerequisites:
edges[x[1]].append(x[0])
state = [0]*numCourses # 0 1 2 未搜索 搜索中 已搜索
has_circle = False
# res_stack = []
def dfs(u):
nonlocal has_circle
state[u]=1
for v in edges[u]:
# print(v, state)
if state[v]==0:
dfs(v)
if has_circle:
return
elif state[v] ==1:
has_circle=True
return
else:
continue
state[u]=2
# res_stack.append()
for i in range(numCourses):
if not has_circle and not state[i]:
dfs(i)
if has_circle:
return False
return True