梯度下降算法(Gradient Descent)的原理和实现步骤 - 知乎 (zhihu.com)
梯度(gradient)到底是个什么东西?物理意义和数学意义分别是什么? - 知乎 (zhihu.com)
目的:最小化损失函数,一个优化的思想
梯度:切点的方向,沿着切线方向前进是最快的(函数值变化最大)
梯度下降:沿着梯度的反方向走
学习率(步长):人为设定,控制梯度下降的步长(初始常见值为0.001、 0.01,结果不好由大到小进行调整,一开始是快速找到收敛方向,后面细致优化防止震荡)
损失函数:当损失函数有多个参数时,要分别优化
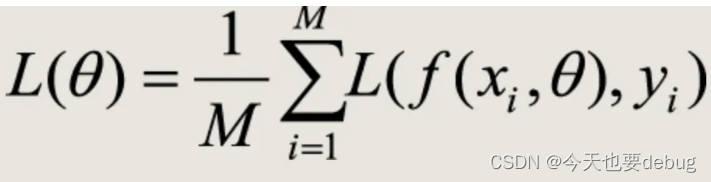
批量梯度下降(GD):
在每次对模型参数进行更新时,需要遍历所有的训练数据
计算过程:要计算所有样本的损失函数梯度,求平均值来更新参数

参数更新:

随机梯度下降(SGD):
会受离散点、噪音点的影响
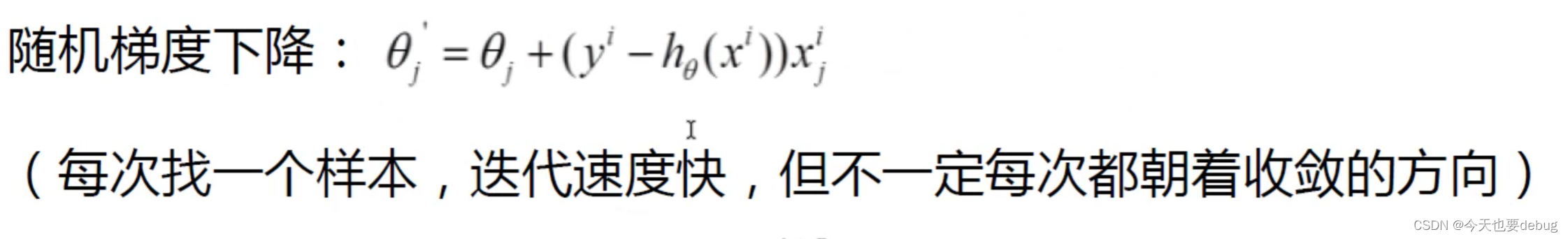
小批量梯度下降(mini-batch GD):
batch表示一次迭代的样本数量,一般取2的幂次时能充分利用矩阵运算操作,常设置为64 128 256,在显卡等允许的前提下越大越好。为了避免数据的特定顺序给算法收敛带来的影响,一般会在每次遍历训练数据之前,先对所有的数据进行随机排序,然后在每次迭代时按顺序挑选m个训练数据直至遍历完所有的数据。

过程:

梯度消失和爆炸:
梯度消失和梯度爆炸及解决方法 - 知乎 (zhihu.com)













![[附源码]Python计算机毕业设计Django财务管理系统](https://img-blog.csdnimg.cn/d6298cada9f44b29815667df310709e4.png)

