0. 简介

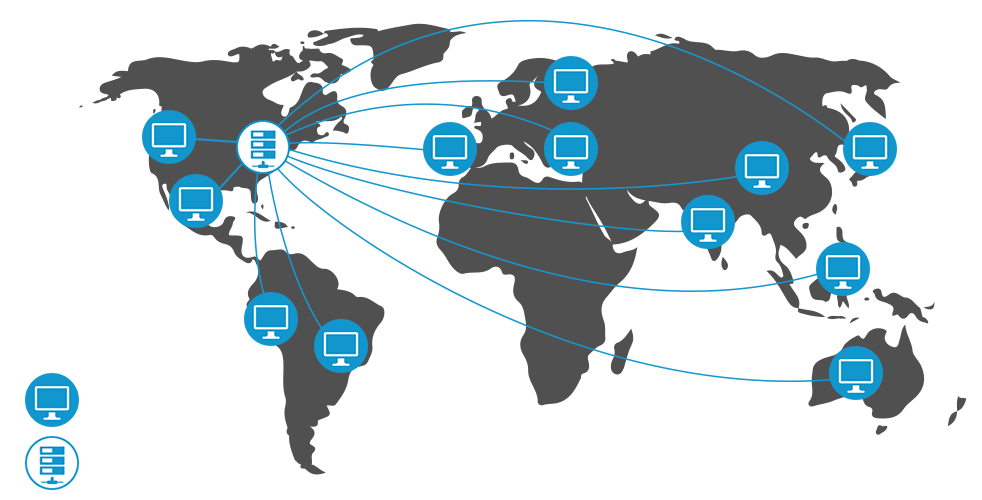
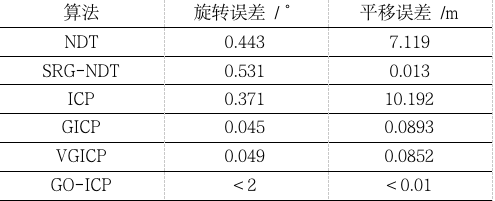
之前我们在以前的文章中介绍了很多有关于点云匹配相关的知识，最近两年处理GICP这一大一统的ICP匹配方法以外，还有一个工作对体素化和ICP这两者打起了心思，《Voxelized GICP for Fast and Accurate 3D Point Cloud Registration》提出了一种体素化的广义迭代最近点（VGICP）算法，用于快速、准确地进行三维点云配准。该方法扩展了广义迭代最近点（GICP）方法的体素化，避免了代价昂贵的最近邻搜索，同时保持了算法的精度。与从点位置计算体素分布的正态分布变换（NDT）不同，我们通过聚集体素中每个点的分布来估计体素分布。体素化方法使算法能够高效地并行处理优化问题，所提出的算法在CPU上可以运行30hz，在GPU上可以运行120hz。通过在模拟环境和真实环境中的评估，我们证实了该算法的精度可以与GICP相媲美，但比现有的方法快得多。结合类ICP和NDT的两者的优点。

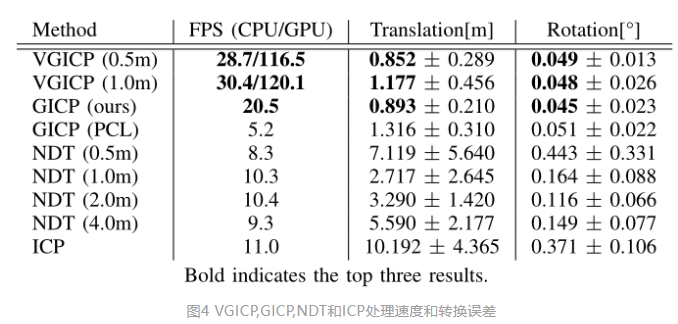
这里深蓝AI的文章中也证明了这一点。

值得一提的是与GICP一样，VGICP也是开源的，开源地址为：https://github.com/SMRT-AIST/fast_gicp.git

1. 文章贡献

三维点云配准是标定、定位、建图和环境重建的等任务中的关键任务。有两种主流的点云配准方法: 广义迭代最近邻方法GICP和正态分布变换NDT方法。GICP算法扩展了经典的ICP算法，通过计算分布到分布的形式提高了配准精度。NDT利用体素化方法避免高昂的最近邻搜索，提高处理速度。由于GICP和其他ICP算法的变种均依赖于最近邻搜索，这使得很难在计算资源受限的计算机中实时的处理大量点云数据。而NDT通常对体素的分辨率大小非常敏感。最佳的体素分辨率取决于环境和传感器属性，如果选择不当的分辨率，则NDT的精度将大幅降低。本文的通过聚合每个体素内所有点的分布，使得体素化的过程更为鲁棒。相比于NDT从点的空间位置估计体素的分布，本文的体素化方法即使体素中有很少的点，也能够产生有效的体素分布。这也使得算法对体素分辨率的改变更加鲁棒。VGICP论文内容写得还是比较详细充实的，从作者的归纳来看论文的贡献有三个方面：

1. 首先，提出了一种多点分布聚合方法来从较少的点稳健估计体素的分布。
2. 其次，提出了VGICP算法，它与GICP一样精确，但比现有方法快得多。
3. 第三，代码开源，并且代码实现了包含了所提出的VGICP以及GICP。
   开源代码中包含有以下几个部分，同时支持ROS

FastGICP: multi-threaded GICP algorithm (~40FPS)
FastGICPSingleThread: GICP algorithm optimized for single-threading (~15FPS)
FastVGICP: multi-threaded and voxelized GICP algorithm (~70FPS)
FastVGICPCuda: CUDA-optimized voxelized GICP algorithm (~120FPS)

2. 具体算法

由于VGICP是由ICP变化而来，这里我们一一来将GICP和VGICP公式之间的对应进行梳理，以方便各位来进行对比：

2.1 初始化

我们考虑变换 $\mathbf{T}$的估计，它将一组点 A = { a 0 , ⋅ ⋅ ⋅ , a N } \mathcal{A}=\lbrace a_0,··· , a_N\rbrace A={a0​,⋅⋅⋅,aN​}（源点云）与另一组点 B = { b 0 , ⋅ ⋅ ⋅ , b N } \mathcal{B}= \lbrace b_0,··· ,b_N\rbrace B={b0​,⋅⋅⋅,bN​}（ 目标点云）。 遵循经典的ICP算法，我们假设A和B之间的对应关系由最近邻搜索给出：$b_i=\mathbf{T}{a}_i$。 GICP 算法 [8] 将采样点的表面建模为高斯分布：$a_i\sim N({\hat{a}}_i,C_i^A),b_i\sim N({\hat{b}}_i,C_i^B)$。 然后，我们定义转换误差如下：
$$d_i^{(T)}=b_i-T{a}_i$$

为了能够推到出VGICP算法，我们首先对式1进行扩展，使得其可以计算点到其邻近点集 { b j ∣ ∥ a i − b j ∥ < r } \left\{b_{j} \mid\left\|a_{i}-b_{j}\right\|<r\right\} {bj​∣∥ai​−bj​∥<r}的距离, 如下

$${\hat{d}}_i^{(T)}=\sum _j(b_j-T{a}_i)$$

2.2 高斯分布

$d_i^{(T)}$的分布由高斯分布的再生特性给出：

$$\begin{array}{rl}{d}_i^{(T)}& \sim \mathcal{N}(\widehat{b_i},C_i^B)-T\mathcal{N}(\widehat{a_i},C_i^A)\\ & =\mathcal{N}(\widehat{b_i}-T\widehat{a_i},C_i^B+(T)C_i^A(T{)}^T)\\ & =\mathcal{N}(0,C_i^B+(T)C_i^A(T{)}^T)\end{array}$$

在VGICP中，这个方程可以解释为平滑目标点分布。类似于$d_i^{(T)}$

$$\begin{array}{rl}{\hat{d}}_i^{(T)}& \sim \mathcal{N}({\mu }^{d_i},C^{d_i})\end{array}$$
$$\begin{array}{r}{\mu }^{d_i}=\sum _j({\hat{b}}_j-\mathbf{T}{\hat{a}}_i)=0\end{array}$$
$$\begin{array}{r}{C}^{d_i}=\sum _j(C_j^B+\mathbf{T}{C}_i^A{\mathbf{T}}^T)\end{array}$$
​

′
的分布由下式给出

2.3 最大化似然概率

GICP 算法找到使方程的对数似然最大化的变换$\mathbf{T}$
$$\begin{array}{rl}T& =\underset{\mathbf{T}}{\mathrm{argmax}}\prod _{i}p(d_i^T)\\ & =\underset{\mathbf{T}}{\mathrm{argmax}}\sum _i\log (p(d_i^{(\mathbf{T})}))\end{array}$$

估计体素化方程的对数似然最大化的变换$\mathbf{T}$如下
$$\begin{array}{rl}T& =\underset{\mathbf{T}}{\mathrm{argmax}}\sum _i(\sum _j(b_j-\mathbf{T}{a}_i){)}^T(\sum _j(C_j^B-\mathbf{T}{C}_i^A{\mathbf{T}}^T){)}^{-1}(\sum _j(b_j-\mathbf{T}{a}_i))\end{array}$$

为了有效地计算上述等式，我们将其修改为

$$\begin{array}{rl}T& =\underset{\mathbf{T}}{\mathrm{argmax}}\sum _i{N}_i(\sum _j(\frac{b_j}{N_i}-\mathbf{T}{a}_i){)}^T(\sum _j(frac{C}_j^B{N}_i-\mathbf{T}{C}_i^A{\mathbf{T}}^T){)}^{-1}(\sum _j(\frac{b_j}{N_i}-\mathbf{T}{a}_i))\end{array}$$

其中$N_i$为邻点的数量。 上式 表明我们可以通过用 $a_i$周围的点 ($b_j$ 和 $C^j$) 的分布的平均值代替GICP等式中的$b_i$和 $C\_i^B$​ 来有效地计算目标函数。 并通过 $N_i$​对函数进行加权。 我们可以通过在每个体素中存储 ${b_i}^{\prime }=\frac{\sum b_j}{N_i}$和${C_i}^{\prime }=\frac{\sum C_j^B}{N_i}$来自然地将该方程应用于基于体素的计算。

…详情请参照古月居