本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
你有一块棋盘,棋盘上有一些格子已经坏掉了。你还有无穷块大小为1 * 2的多米诺骨牌,你想把这些骨牌不重叠地覆盖在完好的格子上,请找出你最多能在棋盘上放多少块骨牌?这些骨牌可以横着或者竖着放。
输入:n, m 代表棋盘的大小;broken是一个b * 2的二维数组,其中每个元素代表棋盘上每一个坏掉的格子的位置。
输出:一个整数,代表最多能在棋盘上放的骨牌数。
示例 1:
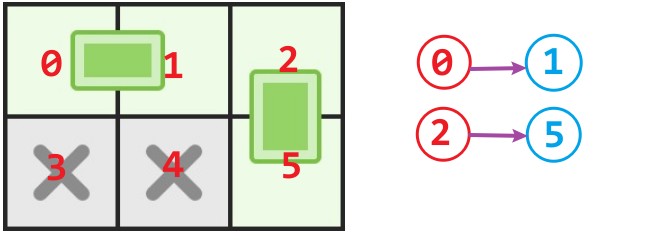
输入:n = 2, m = 3, broken = [[1, 0], [1, 1]]
输出:2
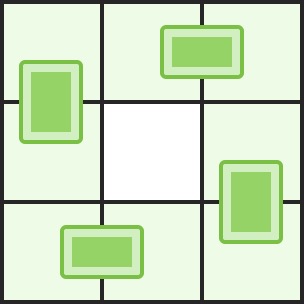
解释:我们最多可以放两块骨牌:[[0, 0], [0, 1]]以及[[0, 2], [1, 2]]。(见下图)
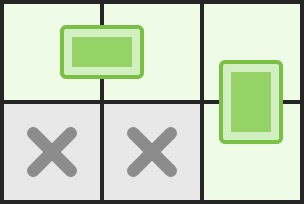
示例 2:
输入:n = 3, m = 3, broken = []
输出:4
解释:下图是其中一种可行的摆放方式
限制:
1 <= n <= 81 <= m <= 80 <= b <= n * m
解法 匈牙利算法
看了标签才做出来,事后诸葛亮还能看出一些使用二分图的迹象:
- 骨牌是1x2的大小,一个骨牌的两个位置一定是相邻的两个位置,这两个位置的下标之和的奇偶性相反。这就抽象成了一个二分图。
- 把奇数点看做男士,偶数点看做女士,建图后就比较直观。
- ==要放置最多的多米诺骨牌,也就是找到一种方式,使得二分图中奇数点和偶数点连起来的边数量最大 ==,这就是典型的二分图最大匹配。
因此,这题就是自行建图后使用匈牙利算法的模板题。
以示例一为例建图:
二分图最大匹配问题,一般可以用匈牙利算法解决。在介绍匈牙利算法之前,需要明确一些专有名词:
- 匹配集合:我们最终的目标是最大化边的数量,这些边将加入匹配集合。
- 匹配边、匹配点:在二分图中,如果本次将两个点连成的边加入匹配集合,就说我们当前将这条边作为了匹配边,边的两个端点均称作匹配点。
- 未匹配边、未匹配点:在二分图中,如果一个点有一条以上的边,并且其中某一条边已经被加入了匹配集合成为了匹配边,那么剩余的边均称作未匹配边,这些边的另一个端点称为未匹配点。
- 增广路:以未匹配边开始和结束,且未匹配边与匹配边交替出现的路径。
为了便于大家理解,通过下图(红框和篮框分别表示二分图中的两部分,黑圆表示不同的点。黄和绿线都表示点之间的边)来解释上面
4
4
4 个概念:
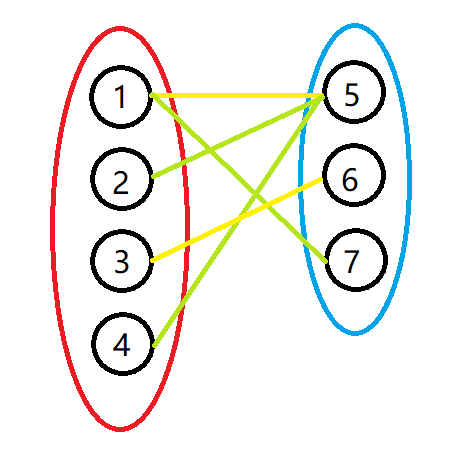
- 首先将 1 1 1 号点和 5 5 5 号点之间的边放入匹配集合,该边就变成了匹配边(黄色标识)。 1 1 1 和 5 5 5 号点就均变为了匹配点,此时,这两个点连接的其他边 ( 1 , 7 ) , ( 2 , 5 ) , ( 4 , 5 ) (1,7),(2,5),(4,5) (1,7),(2,5),(4,5) 就称作未匹配边,对应的点 2 , 4 , 7 2, 4, 7 2,4,7 就均称作未匹配点。
- 其次将 3 3 3 号点和 6 6 6 号点之间的边放入匹配集合,该边就变成了匹配边,这两个点变为了匹配点。由于这两个点没有连其他的边,所以不会出现新的未匹配边。
- 此时发现,路径 2 − 5 − 1 − 7 2-5-1-7 2−5−1−7 就是一条 未匹配边-匹配边-未匹配边 组合的增广路径。
明确了这些概念后,看匈牙利算法:
- 初始时,最大匹配集合为空。
- 我们先找到一组匹配边,加入匹配集合。
- 如果找到一条增广路径,就将其中的所有匹配边变为未匹配边,将所有的未匹配边变为匹配边。
- 循环步骤 3 3 3 ,直到图中不存在增广路径。算法结束。
匈牙利算法中,最重要的便是步骤
3
3
3 。深入理解——对于一条增广路径,根据其定义,必定含有
k
+
1
k + 1
k+1 条未匹配边以及
k
k
k 条匹配边。那么,步骤
3
3
3 的作用,其实就是将未匹配边和匹配边互换,这样,==该路径上就会更新为
k
k
k 条未匹配边以及
k
+
1
k + 1
k+1 条匹配边,匹配边的数量就比互换之前多了
1
1
1 ==。
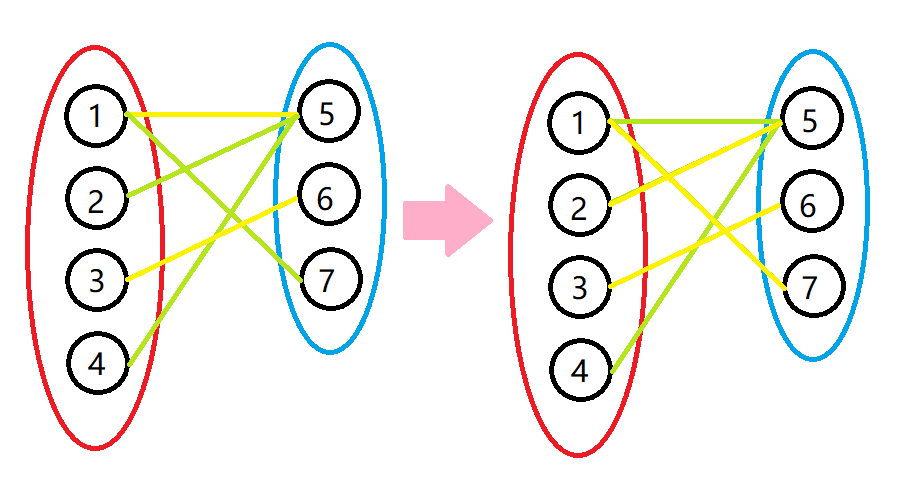
结合刚才的图片来看:我们将增广路径
2
−
5
−
1
−
7
2-5-1-7
2−5−1−7 上的未匹配边
(
2
,
5
)
,
(
1
,
7
)
(2,5),(1,7)
(2,5),(1,7) 变为匹配边,将匹配边
(
5
,
1
)
(5,1)
(5,1) 变为未匹配边,图中总匹配边数就从原来的两条
(
1
,
5
)
,
(
3
,
6
)
(1,5),(3,6)
(1,5),(3,6) 变成了三条
(
2
,
5
)
,
(
1
,
7
)
,
(
3
,
6
)
(2, 5), (1, 7), (3, 6)
(2,5),(1,7),(3,6) 。
一开始建二分图时,我们需要将题目给定的图标识成二分图(比如一部分标识为 0 0 0 ,另一部分标识为 1 1 1 )。但在本题中,棋盘上第 i i i 行第 j j j 列属于哪一部分可以直接根据 i + j i+j i+j 的奇偶性得到。
特别地,在二分图中,只需要从一个集合向另一个集合连有向边即可,不需要双向连边(虽然代码中随手写的双向连边)。另外,本题中棋盘上有些点不可以放多米诺骨牌,在连边过程中进行特判即可。
class Solution {
public:
int domino(int n, int m, vector<vector<int>>& broken) {
vector<int> g[100];
bool vis[100] = {false};
bool b[100] = {false};
int match[100];
int ans = 0;
function<bool(int)> dfs = [&](int u) -> bool {
for (int v : g[u]) {
if (!vis[v]) { // 没访问过
vis[v] = true; // 避免重复访问, 能让就让
if (match[v] == -1 || dfs(match[v])) {
match[v] = u; return true;
}
}
}
return false;
};
for (vector<int> &bv : broken) // 哪些位置破损
b[bv[0] * m + bv[1]] = true;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < m; ++j) {
int u = i * m + j;
if (b[u]) continue;
int v1 = i * m + j + 1, v2 = (i + 1) * m + j;
if (j + 1 < m && !b[v1]) { // 只存奇数点到偶数点的边也行
g[u].push_back(v1);
g[v1].push_back(u);
}
if (i + 1 < n && !b[v2]) {
g[u].push_back(v2);
g[v2].push_back(u);
}
}
}
memset(match, -1, sizeof(match));
for (int i = 0, t = n * m; i < t; ++i) {
int x = i / m, y = i % m;
memset(vis, false, size(vis));
if (((x + y) & 1) && !b[i] && !vis[i] && dfs(i)) // 从奇数点出发向偶数点连边
++ans;
}
return ans;
}
};