13463 - 折点计数(难题!重点题!)
时间限制 : 1 秒
内存限制 : 128 MB
给定 n 个整数表示一个商店连续 n 天的销售量。 如果某天之前销售量在增长,而后一天销售量减少,则称这一天为折点,反过来如果之前销售量减少而后一天销售量增长,也称这一天为折点。 其他的天都不是折点。 如下图中,第 3 天和第 6 天是折点。
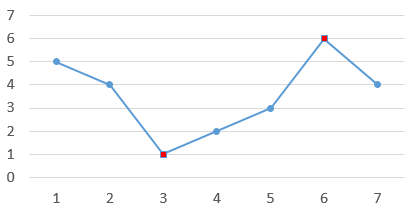
给定 n 个整数 a1,a2,…,an 表示销售量,请计算出这些天总共有多少个折点。 为了减少歧义,我们给定的数据保证:在这 n 天中相邻两天的销售量总是不同的,即 ai−1≠ai。 注意,如果两天不相邻,销售量可能相同。
输入
输入的第一行包含一个整数 n。 第二行包含 n 个整数,用空格分隔,分别表示 a1,a2,…,an。
所有评测用例满足:1≤n≤1000,每天的销售量是不超过 10000 的非负整数。
输出
输出一个整数,表示折点出现的数量。
样例
输入
7 5 4 1 2 3 6 4
输出
2
答案:
#include<iostream>
using namespace std;
int main() {
int n;
int Flag = -1;//Falg是用来判断当前折线是处于上升还是处于下滑,1表示上升,0表示下滑
int isFlat = -1;//isFlat用来判断折线是否是平坦,1平坦,0不平坦
int upCount = 0, downCount = 0;
cin >> n;
int a[10000];
for (int i = 0; i < n; i++) {
cin >> a[i];
}
for (int i = 0; i < n-1; i++) {
if (a[i + 1] - a[i] < 0 && Flag == 1 && isFlat == 0) {//处于上升状态,发生下滑,且当前状态不是平坦状态
upCount++;
Flag = 0;//突然下滑
isFlat = 0;
}
else if (a[i + 1] - a[i] > 0 && Flag == 0 && isFlat == 0) {//处于下滑状态,发生上升,且当前状态不是平坦状态
downCount++;
Flag = 1;//突然上升
isFlat = 0;
}
else if (a[i + 1] - a[i]>0) {
Flag = 1;//正在上升
isFlat = 0;
}
else if (a[i + 1] - a[i] < 0) {
Flag = 0;//正在下滑
isFlat = 0;
}
else {//a[i+1]-a[i]==0,当前是平坦状态
isFlat = 1;
}
}
int sum = upCount + downCount;
cout << sum << endl;
return 0;
}分析:这个题还是有点难度的。
1、首先要判断当前折线的状态,上升,下滑,还有平坦。
2、只有上升到下滑的跳变或者下滑到上升的跳变才是折点。平坦到上升,或者平坦到下滑这个不是折点!!这也是本题测试点最后一个。我最开始没考虑到这种情况。
是否通过:

13464 - 画图(重点题,二刷!)
输出
输出一个整数,表示有多少个单位的面积被涂上颜色。
样例
输入
2 1 1 4 4 2 3 6 5
输出
15
答案:
#include <iostream>
using namespace std;
#define MAX 101
int main(void)
{
int a[MAX][MAX] = { 0 };
int n;
int x1, y1, x2, y2;//两个点的坐标
cin >> n;
for (int k = 0; k < n; k++)
{
cin >> x1 >> y1 >> x2 >> y2;
for (int i = x1; i < x2; i++) {//思考为什么这样写?
for (int j = y1; j < y2; j++)//理解这个代码思想真的是太漂亮了
a[i][j] = 1;
}
}
int sum = 0;
for (int i = 0; i < MAX; i++) {
for (int j = 0; j < MAX; j++) {
if (a[i][j] == 1)
sum++;
}
}
cout << sum<< endl;
return 0;
}分析:这个题难度比较大,我最开始以为要把所有矩形依次比较,然后每两两矩形分别找出重叠的矩形,最后减去这鞋重叠的正方形个数即为所求的正方形个数。但是这样把问题就复杂了很多。整道题的解法很巧妙。当只有一个正方形时:比如坐标为(1,1)和(4,4)

这个矩形一共有9个小正方形被图色。9个小正方形被涂色,我们可以怎么表示呢?如下:

我们只需要把这些点标记为已经涂色即可。也就是横坐标i从x1起,直到x2-1,纵坐标从y1起,直到y2-1。
同理如果是两个矩形,分别对两个矩形做这样的处理,中间重叠的图形就直接用这些点表示即可。最后统计的时候只需要知道那些点坐标已经图上色就统计即可。
是否通过:
21304 - 求矩阵的转置
时间限制 : 1 秒
内存限制 : 128 MB
二维矩阵的转置,将给定的一个二维数组(3×3)转置,即行列互换。
输入
一个3x3的矩阵
输出
转置后的矩阵
样例
输入
1 2 3 4 5 6 7 8 9
输出
1 4 7 2 5 8 3 6 9
答案:
#include<iostream>
using namespace std;
int main() {
int a[3][3];
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cin >> a[i][j];
}
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < i; j++) {
int temp = a[i][j];
a[i][j] = a[j][i];
a[j][i] = temp;
}
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
cout << a[i][j] << ' ';
}
cout << endl;
}
return 0;
}分析:这个题本身不难,但是下标从0计算的话还是容易有点迷惑。转置的意思就是a[i][j]和a[j][i]交换即可。
是否通过:

21305 - 寻找鞍点(重点题)
时间限制 : 1 秒
内存限制 : 128 MB
求一个5*5的矩阵的鞍点。鞍点指的是矩阵中的一个元素,它是所在行的最大值,并且是所在列的最小值。例如:在下面的例子中(第3行第0列的元素就是鞍点,值为8 )。
11 3 5 6 9
12 4 7 8 10
10 5 6 9 11
8 6 4 7 2
15 10 11 20 25
输入
输入包含一个5行5列的矩阵
输出
如果存在鞍点,输出鞍点所在的行、列及其值(题目中每个输入都只有一个鞍点);如果不存在,输出not found
样例
输入
11 3 5 6 9 12 4 7 8 10 10 5 6 9 11 8 6 4 7 2 15 10 11 20 25
输出
3 0 8
答案:
#include<iostream>
using namespace std;
int main() {
int a[5][5];
//输入数据
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
cin >> a[i][j];
}
}
int max[5] = { 0 }, min[5] = { 0 };
//分别求出每行的最大值和每列的最小值
for (int i = 0; i < 5; i++) {
max[i] = a[i][0];
min[i] = a[0][i];
for (int j = 0; j < 5; j++) {
//求该元素所在行的最大值
max[i] = max[i] > a[i][j] ? max[i] : a[i][j];
//求该元素所在列的最小值
min[i] = min[i] < a[j][i] ? min[i] : a[j][i];
}
}
bool flag = false;//为true表示找到鞍点,为false表示矩阵中没有鞍点
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 5; j++) {
if (max[i] == a[i][j] && min[j] == a[i][j]) {
flag = true;
cout << i << ' ' << j << ' ' << a[i][j] << endl;
break;
}
}
}
if (flag == false) {
cout << "not found" << endl;
}
return 0;
}分析:这个题还是比较难的,当时刚学习C语言的时候就有这道题,感觉是完全不会,无从下手,但是随着不断学习和练习,现在发现这道题也不是那么难。主要思路就是找到每一行的最大值和每一列的最小值。然后判断每个元素是否即等于当前所在行的最大值又等于当前所在列的最小值。则这个点就是鞍点。
是否通过:

21306 - 杨辉三角形(重点题)
时间限制 : 1 秒
内存限制 : 128 MB
杨辉三角形,又称贾宪三角形、帕斯卡三角形,是二项式系数在三角形中的一种几何排列。杨辉三角形同时对应于二项式定理的系数。n次的二项式系数对应杨辉三角形的n + 1行。
输入
n(杨辉三角的行,1 <= n <= 20)
输出
行数为n的杨辉三角图形(数字与数字间使用空格隔开) 样例输入
样例
输入
3
输出
1 1 1 1 2 1
答案:
#include<iostream>
using namespace std;
int main() {
int n;
cin >> n;
int a[21][21] = { 0 };
//计算三角形每个元素的值
for (int i = 1; i <= n; i++) {
a[i][1] = 1;
a[i][i] = 1;
for (int j = 1; j <= i - 1; j++) {
a[i][j] = a[ i- 1][j - 1] + a[i - 1][j];
}
}
//打印
for (int i = 1; i <= n; i++) {
//先打印空格
for (int j = 1; j <= n - i; j++) {
cout << ' ';
}
//打印数据
for (int k = 1; k <= i; k++) {
cout << a[i][k] << ' ';
}
cout << endl;
}
return 0;
}分析:这是一个非常经典的问题,首先不要被打印的那个样式给唬住了,杨辉三角的正常形式是如下的样子:

即对每一行元素有如下:
a[i][1]=1;
a[i][i]=1;
对其他元素有满足:
a[i][j]=a[i-1][i-1][j];
计算出三角形的值,然后按指定格式打印。对打印这个三角形我想再熟悉不过了,嵌套循环,嵌套两个循环做两个不同的事。这是之前刷打印三角形就掌握的。不理解的刷刷前面打印三角形那个题。
是否通过: