基于鲸鱼算法的极限学习机(ELM)回归预测
文章目录
- 基于鲸鱼算法的极限学习机(ELM)回归预测
- 1.极限学习机原理概述
- 2.ELM学习算法
- 3.回归问题数据处理
- 4.基于鲸鱼算法优化的ELM
- 5.测试结果
- 6.参考文献
- 7.Matlab代码
摘要:本文利用鲸鱼算法对极限学习机进行优化,并用于回归预测
1.极限学习机原理概述
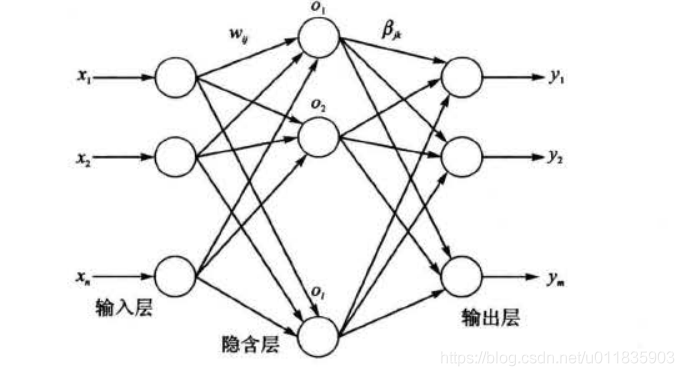
典型的单隐含层前馈神经网络结构如图1 所示,由输入层、隐含层和输出层组成,输 入层与隐含层、隐含层与输出层神经元间全连接。其中,输入层有 n 个神经元,对应 n 个输入变量, 隐含层有 l个神经元;输出层有 m 个神经元 ,对应 m 个输出变量 。 为不失一般性,设输 入层与隐含层间的连接权值 w 为:
w
=
[
w
11
w
12
.
.
.
w
1
,
n
w
21
w
22
.
.
.
w
2
n
.
.
.
w
l
1
w
l
2
.
.
.
w
l
n
]
(1)
w =\left[\begin{matrix}w_{11}&w_{12}&...&w_{1,n}\\ w_{21}&w_{22}&...&w_{2n}\\ ...\\ w_{l1}&w_{l2}&...&w_{ln} \end{matrix}\right]\tag{1}
w=
w11w21...wl1w12w22wl2.........w1,nw2nwln
(1)
其中,
w
n
w_n
wn表示输入层第
i
i
i个神经元与隐含层第
j
j
j个神经元间的连接权值。
设隐含层与输出层间的连接权值 , 为
β
\beta
β:
β
=
[
β
11
β
12
.
.
.
β
1
m
β
21
β
22
.
.
.
β
2
m
.
.
.
β
l
1
β
l
2
.
.
.
β
l
m
]
(2)
\beta =\left[\begin{matrix} \beta_{11}&\beta_{12}&...&\beta_{1m}\\ \beta_{21}&\beta_{22}&...&\beta_{2m}\\ ...\\ \beta_{l1}&\beta_{l2}&...&\beta_{lm} \end{matrix}\right] \tag{2}
β=
β11β21...βl1β12β22βl2.........β1mβ2mβlm
(2)
其中,自
β
j
k
\beta_{jk}
βjk表示隐含层第 j 个神经元与输出层第 k个神经元间的连接权值。
设隐含层神经元的阈值值 b 为:
b
=
[
b
1
b
2
.
.
.
b
l
]
(3)
b =\left[\begin{matrix}b_1\\ b_2\\ ...\\ b_l \end{matrix}\right]\tag{3}
b=
b1b2...bl
(3)
设具有 Q 个样本的训练集输入矩阵 X 和输出矩阵 Y 分别为
X
=
[
x
11
x
12
.
.
.
x
1
Q
x
21
x
22
.
.
.
x
2
Q
.
.
.
x
n
1
x
n
2
.
.
.
x
n
Q
]
(4)
X =\left[\begin{matrix}x_{11}&x_{12}&...&x_{1Q}\\ x_{21}&x_{22}&...&x_{2Q}\\ ...\\ x_{n1}&x_{n2}&...&x_{nQ} \end{matrix}\right]\tag{4}
X=
x11x21...xn1x12x22xn2.........x1Qx2QxnQ
(4)
KaTeX parse error: Undefined control sequence: \matrix at position 11: Y =\left[\̲m̲a̲t̲r̲i̲x̲{y_{11},y_{12},…
设隐含层神经元的激活函数为 g(x),则由图1 可得, 网络的输出 T 为:
T
=
[
t
1
,
.
.
,
t
Q
]
m
∗
Q
,
t
j
=
[
t
1
j
,
.
.
.
,
t
m
j
]
T
=
[
∑
i
=
1
t
β
i
1
g
(
w
i
x
j
+
b
i
)
∑
i
=
1
t
β
i
2
g
(
w
i
x
j
+
b
i
)
.
.
.
∑
i
=
1
t
β
i
m
g
(
w
i
x
j
+
b
i
)
]
m
∗
1
,
(
j
=
1
,
2
,
.
.
.
,
Q
)
(6)
T = [t_1,..,t_Q]_{m*Q},t_j = [t_{1j},...,t_{mj}]^T =\left[\begin{matrix}\sum_{i=1}^t\beta_{i1}g(w_ix_j + b_i)\\ \sum_{i=1}^t\beta_{i2}g(w_ix_j + b_i)\\ ...\\ \sum_{i=1}^t\beta_{im}g(w_ix_j + b_i) \end{matrix}\right]_{m*1},(j=1,2,...,Q)\tag{6}
T=[t1,..,tQ]m∗Q,tj=[t1j,...,tmj]T=
∑i=1tβi1g(wixj+bi)∑i=1tβi2g(wixj+bi)...∑i=1tβimg(wixj+bi)
m∗1,(j=1,2,...,Q)(6)
式(6)可表示为:
H
β
=
T
’
(7)
H\beta = T’ \tag{7}
Hβ=T’(7)
其中, T’为矩阵 T 的转置; H 称为神经网络的隐含层输出矩阵 , 具体形式如下 :
H
(
w
1
,
.
.
.
,
w
i
,
b
1
,
.
.
.
,
b
l
,
x
1
,
.
.
.
,
x
Q
)
=
[
g
(
w
1
∗
x
1
+
b
1
)
g
(
w
2
∗
x
1
+
b
2
)
.
.
.
g
(
w
l
∗
x
1
+
b
l
)
g
(
w
1
∗
x
2
+
b
1
)
g
(
w
2
∗
x
2
+
b
2
)
.
.
.
g
(
w
l
∗
x
2
+
b
l
)
.
.
.
g
(
w
1
∗
x
Q
+
b
1
)
g
(
w
2
∗
x
Q
+
b
2
)
.
.
.
g
(
w
l
∗
x
Q
+
b
l
)
]
Q
∗
l
H(w_1,...,w_i,b_1,...,b_l,x_1,...,x_Q) =\left[\begin{matrix} g(w_1*x_1 + b_1)&g(w_2*x_1 + b_2)&...&g(w_l*x_1 + b_l)\\ g(w_1*x_2 + b_1)&g(w_2*x_2 + b_2)&...&g(w_l*x_2 + b_l)\\ ...\\ g(w_1*x_Q + b_1)&g(w_2*x_Q + b_2)&...&g(w_l*x_Q + b_l) \end{matrix}\right]_{Q*l}
H(w1,...,wi,b1,...,bl,x1,...,xQ)=
g(w1∗x1+b1)g(w1∗x2+b1)...g(w1∗xQ+b1)g(w2∗x1+b2)g(w2∗x2+b2)g(w2∗xQ+b2).........g(wl∗x1+bl)g(wl∗x2+bl)g(wl∗xQ+bl)
Q∗l
2.ELM学习算法
由前文分析可知,ELM在训练之前可以随机产生 w 和 b , 只需确定隐含层神经元个数及隐含层和神经元的激活函数(无限可微) , 即可计算出 β \beta β 。具体地, ELM 的学习算法主要有以下几个步骤:
(1)确定隐含层神经元个数,随机设定输入层与隐含层间的连接权值 w 和隐含层神经元的偏置 b ;
(2) 选择一个无限可微的函数作为隐含层神经元的激活函数,进而计算隐含层输出矩 阵 H ;
(3)计算输出层权值: β = H + T ′ \beta = H^+T' β=H+T′
值得一提的是,相关研究结果表明,在 ELM 中不仅许多非线性激活函数都可以使用(如 S 型函数、正弦函数和复合函数等),还可以使用不可微函数,甚至可以使用不连续的函数作为激 活函数。
3.回归问题数据处理
采用随机法产生训练集和测试集,其中训练集包含 1 900 个样 本,测试集包含 100 个样本。为了减少变量差异较大对模型性能的影响,在建立模型之前先对数据进行归一化。
4.基于鲸鱼算法优化的ELM
鲸鱼算法的具体原理参考博客:https://blog.csdn.net/u011835903/article/details/107559167
由前文可知,ELM的初始权值和阈值都是随机产生。每次产生的初始权值和阈值具有满目性。本文利用鲸鱼算法对初始权值和阈值进行优化。适应度函数设计为训练集的误差的MSE:
f
i
t
n
e
s
s
=
a
r
g
m
i
n
(
M
S
E
p
r
i
d
e
c
t
)
fitness = argmin(MSE_{pridect})
fitness=argmin(MSEpridect)
适应度函数选取训练后的MSE误差。MSE误差越小表明预测的数据与原始数据重合度越高。最终优化的输出为最佳初始权值和阈值。然后利用最佳初始权值阈值训练后的网络对测试数据集进行测试。
5.测试结果
鲸鱼算法相关参数如下:
%训练数据相关尺寸
R = size(Pn_train,1);
S = size(Tn_train,1);
N = 20;%隐含层个数
%% 定义鲸鱼优化参数
pop=20; %种群数量
Max_iteration=50; % 设定最大迭代次数
dim = N*R + N*S;%维度,即权值与阈值的个数
lb = [-1.*ones(1,N*R),zeros(1,N*S)];%下边界
ub = [ones(1,N*R),ones(1,N*S)];%上边界
将经过鲸鱼优化后的ELM与基础ELM进行对比。
预测结果如下图
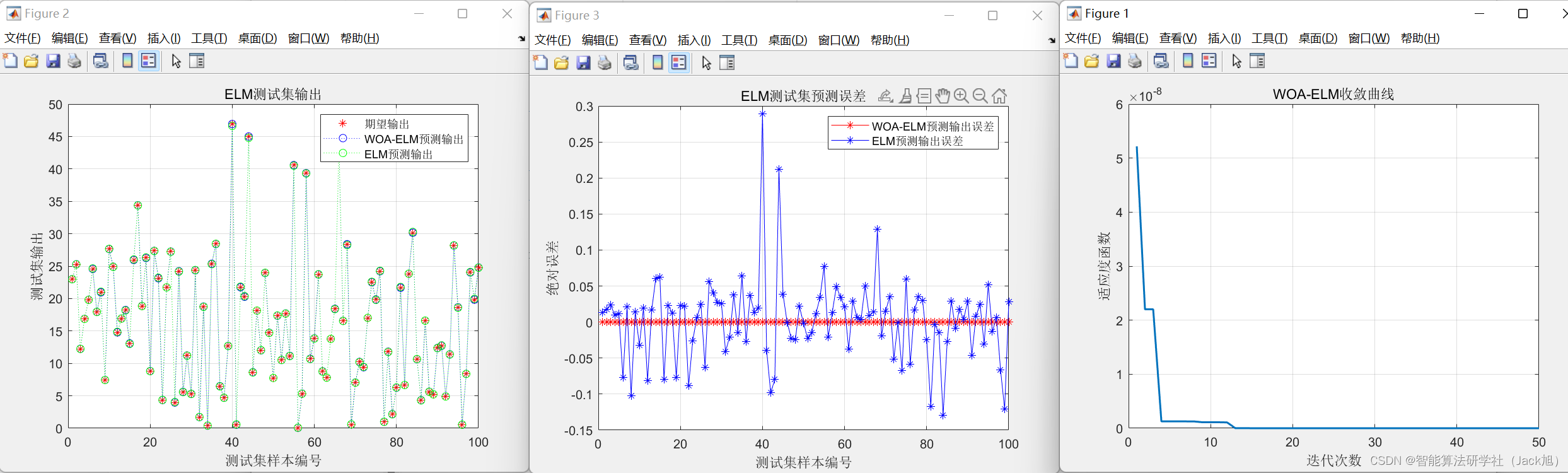
基础ELM MSE误差:0.0034066
WOA-ELM MSE误差:9.1593e-12
从MSE看,鲸鱼-ELM明显优于基础ELM
6.参考文献
书籍《MATLAB神经网络43个案例分析》