目录

一、二叉树的创建

二、二叉树的遍历

1.前序中序后序遍历

2.层序遍历

三、二叉树的节点个数以及高度等

四、二叉树的构建和销毁

五、DFS和BFS

---

一、二叉树的创建

为了方便后面的讨论，我们在这里先手撕一颗二叉树

typedef int BTDateType;
typedef struct BinaryTreeNode
{
	BTDateType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

//生成一个二叉树节点
BTNode* BuyNode(BTDateType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		return NULL;
	}
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;

	return newnode;
}

//生成一颗二叉树
BTNode* CreatBinaryTree()
{
	BTNode* n1 = BuyNode(1);
	BTNode* n2 = BuyNode(2);
	BTNode* n3 = BuyNode(3);
	BTNode* n4 = BuyNode(4);
	BTNode* n5 = BuyNode(5);
	BTNode* n6 = BuyNode(6);

	n1->left = n2;
	n1->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;

	return n1;
}

注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后文讲解

二叉树是：

1. 空树

2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

二、二叉树的遍历

1.前序中序后序遍历

学习二叉树结构，最简单的方式就是遍历。所谓 二叉树遍历 (Traversal) 是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次 。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。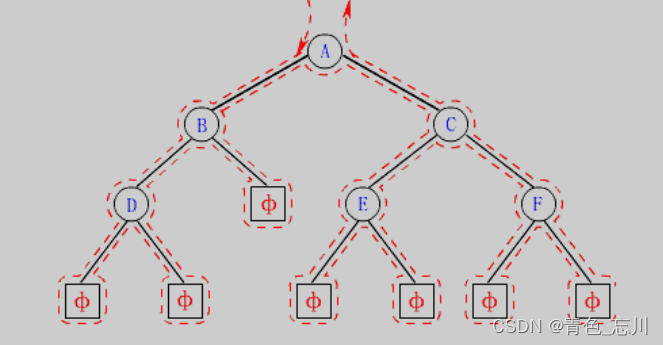

按照规则，二叉树的遍历有： 前序 / 中序 / 后序的递归结构遍历 ：

1. 前序遍历 (Preorder Traversal 亦称先序遍历 )—— 访问根结点的操作发生在遍历其左右子树之前。

2. 中序遍历 (Inorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之中（间）。

3. 后序遍历 (Postorder Traversal)—— 访问根结点的操作发生在遍历其左右子树之后。

由于被访问的结点必是某子树的根， 所以 N(Node ）、 L(Left subtree ）和 R(Right subtree ）又可解释为 根、根的左子树和根的右子树 。 NLR 、 LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。

如下图所示，是二叉树的先序中序后序的图解

二叉树的先序中序后序代码为如下所示

//二叉树的先序遍历
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->data);
	PreOrder(root->left);
	PreOrder(root->right);
}
//二叉树的中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf("%d ", root->data);
	InOrder(root->right);
}
//二叉树的后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");
	return 0;
}

2.层序遍历

二叉树的层序遍历值得是一层一层的将数据给遍历下来。

为了一层一层的遍历，我们必须得借助队列才能实现。我们的思想是这样的，一开始先让根节点入队列。然后当队列不为空的时候，将队头出队列，然后将二叉树的左孩子和右孩子入队列。然后打印队头的数据。这样一直循环下去，每出一个节点，都需要入两个孩子。当然如果孩子为空，就没有必要入队列了。直到将队列出光，正好也就打印完了。

这里我们需要注意的是，当我们的队列代码复制到二叉树中的时候，我们需要将队中数据的类型修改为二叉树结点指针类型。

 

//二叉树的层序遍历
void LevelOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ", front->data);
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
	}
	QueueDestroy(&q);
}

三、二叉树的节点个数以及高度等

1.二叉树的计算节点个数

//二叉树的节点个数
void TreeSize1(BTNode* root, int* psize)
{
	if (root == NULL)
	{
		return;
	}
	(*psize)++;
	TreeSize1(root->left, psize);
	TreeSize1(root->right, psize);
}
int TreeSize2(BTNode* root)
{
	return root == NULL ? 0 : 1 + TreeSize2(root->left) + TreeSize2(root->right);
}
int main()
{
	BTNode* root = CreatBinaryTree();
	PreOrder(root);
	printf("\n");
	InOrder(root);
	printf("\n");
	PostOrder(root);
	printf("\n");

	int size1 = 0;
	TreeSize1(root, &size1);
	printf("TreeSize1:%d\n", size1);
	int size2 = 0;
	TreeSize1(root, &size2);
	printf("TreeSize1:%d\n", size2);

	printf("TreeSize2:%d\n", TreeSize2(root));
	return 0;
}

如上代码所示，是二叉树的节点个数的计算，有两种方式可以实现，一种是使用一个指针，然后传参，将数都累加在指针所指向的变量上。

另外一种是采用分治的思想，分而治之，这颗树的结点个数等于 1+左子树+右子树

2.二叉树的高度

//二叉树的高度
int TreeHeight(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int LeftHeight = TreeHeight(root->left);
	int RightHeight = TreeHeight(root->right);
	int ChildHeight = LeftHeight > RightHeight ? LeftHeight : RightHeight;
	return 1 + ChildHeight;
}

如上代码所示，我们仍然采用双路递归，如果根节点为空，那么高度为0，否则计算左子树和右子树的中最大的那个高度，然后加1返回即可

3.二叉树第k层的节点个数

//二叉树第k层的节点个数
int TreeLevel(BTNode* root, int k)
{
	assert(k > 0);
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return TreeLevel(root->left, k - 1) + TreeLevel(root->right, k - 1);
}

如上代码所示，这道题的关键核心是，根节点的第k层的节点个数可以转化为左子树第k-1层的节点个数加上右子树第k-1层的节点个数。还有一点就是递归的结束条件，如果树为空，返回0，如果为第一层，则返回1即可

4.二叉树查找一个值为x的节点

//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDateType x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	BTNode* left = TreeFind(root->left, x);
	if (left != NULL)
	{
		return left;
	}
	BTNode* right = TreeFind(root->right, x);
	if (right != NULL)
	{
		return right;
	}
	return NULL;
}

我们先判断这颗树是否为空，如果为空，那么直接返回NULL，然后再判断当前节点是否为x，如果是，返回即可。最后我们再找一下左子树，然后找一下右子树，如果都没有找到，那就返回NULL

5.二叉树的叶子结点个数

//二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left || root->right)
	{
		return TreeLeafSize(root->left) + TreeLeafSize(root->right);
	}
	else
	{
		return 1;
	}
}

如上代码所示，我们先判断根节点，如果根节点为空，直接返回0，如果左孩子和右孩子只要有一个不为空，那么就计算左子树和右子树的结点个数。如果左右孩子都为空，那么返回1

四、二叉树的构建和销毁

1.二叉树的构建

这里我们使用这道题来完成这个接口：二叉树遍历_牛客题霸_牛客网

#include <stdio.h>
#include<stdlib.h>
typedef struct TreeNode
{
    struct TreeNode* left;
    struct TreeNode* right;
    char val;
}TreeNode;
TreeNode* CreatTree(char* a,int* pi)
{
    if(a[*pi]=='#')
    {
        (*pi)++;
        return NULL;
    }
    TreeNode* root=(TreeNode*)malloc(sizeof(TreeNode));
    root->val=a[(*pi)++];
    root->left=CreatTree(a,pi);
    root->right=CreatTree(a,pi);
    
    return root;
}
void InOrder(TreeNode* root)
{
    if(root==NULL)
    {
        return;
    }
    InOrder(root->left);
    printf("%c ",root->val);
    InOrder(root->right);
}
int main() {
    char a[101]={0};
    scanf("%s",a);
    int i=0;
    TreeNode* root=CreatTree(a,&i);
    InOrder(root);
    return 0;
}

这个接口也不难理解，我们根据先判断当前的字符是否为'#'，如果是则返回NULL，否则就创建好一个节点，然后开始递归创建左子树和右子树

2.判断一棵树是否为完全二叉树

我们可以利用层序的思路，完全二叉树的特点就是，层序遍历出现第一个NULL的时候，以后都是NULL了，所以我们这样做，当第一次出现NULL的时候，我们先跳出这个循环，然后从后面开始不断出队判断是否存在不为空的结点。一旦存在直接返回false。

//判断一颗二叉树是否为完全二叉树
bool TreeComplete(BTNode* root)
{
	if (root == NULL)
		return true;
	Queue q;
	QueueInit(&q);
	QueuePush(&q, root);
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			break;
		}
	}
	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

3.二叉树的销毁

//二叉树的销毁
void TreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}
	TreeDestory(root->left);
	TreeDestory(root->right);
	free(root);
	root = NULL;
}

对于二叉树的销毁，我们需要注意的是最好使用后序遍历销毁，如果采用前序中序的话，我们就必须得创建临时变量了，这样就非常繁琐。

五、DFS和BFS

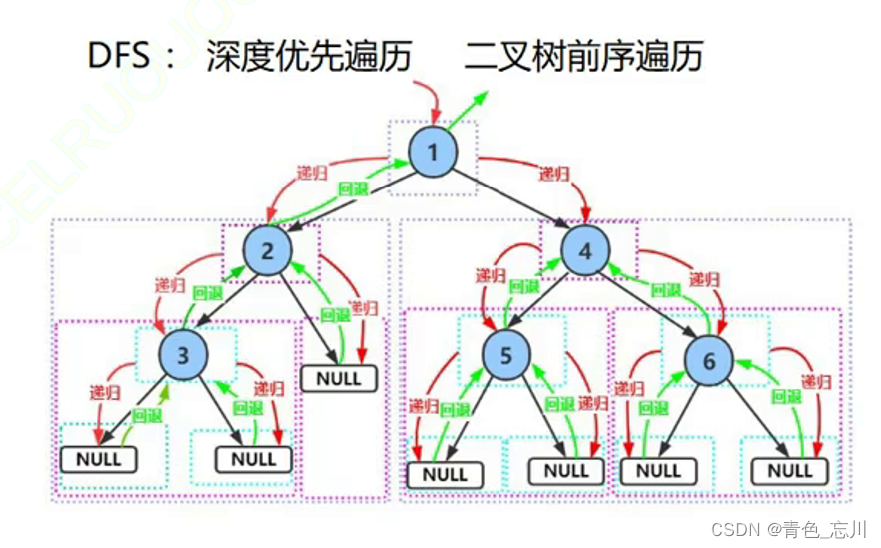
1.DFS:深度优先遍历

对于二叉树而言，他的深度优先遍历其实就是先序遍历，当然如果不是很严格的话中序和后序也算深度优先遍历。因为中序和后序的递归过程与先序是一样的，只不过是根节点的时机不一样

 但是要注意，不能说先序遍历就是深度优先遍历，因为深度优先遍历还包括图，二维数组等的遍历。只能说二叉树的前序遍历是深度优先遍历或二叉树的深度优先遍历是前序遍历

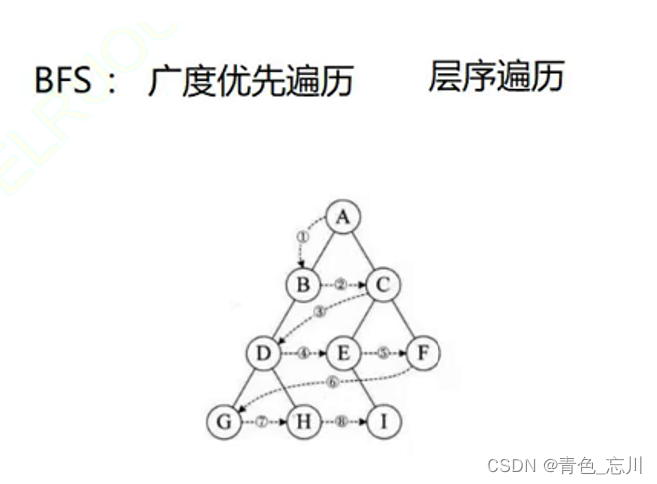
2.BFS:广度优先遍历

对于二叉树而言，他的广度优先遍历就是层序遍历

 

---

本节内容到此位置

如果对你有帮助的话，不要忘记点赞加收藏哦！！！