前言

尽管计算机是门严谨的学科，但正因为严谨，所以要有趣味才能看得下去。在笔者的前几篇算法类文章中，都采用了以小故事作为引入的方式来介绍算法，但在回看的时候发现学术味还是太浓了，完全没有想看下去的欲望orz~因此笔者决定改组文章结构，将整个算法都以故事的形式呈现，至少让读者能看下去，希望能帮助到大家！

正文

小明的探险之旅（2）

上文说到小明从家中收拾好装备后，就踏上了茫茫星海的探险征程。在航行了数天后，他到达了第一个星球——食戟之星。这颗星球以昂贵而美味的食物而著称，由于小明实在太饿，他直接钻进了一家自助餐店，想好好的回回血。

小明看着这些食物不禁直流口水：这么多好吃的，都好想吃！可是怎么吃才能吃的最好呢。。（注：小明吃好的标准是吃到的所有食物价格总和最高，也就是最能回本）

（小明思考了一会）

小明：感觉这个问题和我搬装备时候的问题很像，但是这次所有食物都是无限供应的。。先想一想之前用到的转移方程吧！
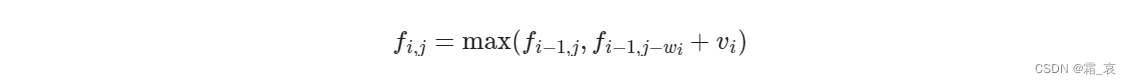
在这里插入图片描述

那么，之前的装备一种只有一件，而这次的食物有无数件，也就是说，不一定是j-w[i]，也可以是j-2w[i]，j-3w[i]……所以就是
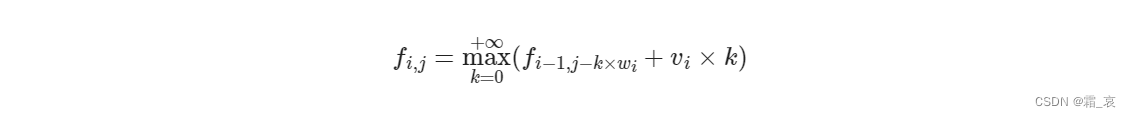
在这里插入图片描述
可是这样的话，时间复杂度就太大了……就算用了滚动数组优化，也会到达平方级的时间复杂度，还要进行复杂的边界判断……

（小明陷入了苦想，直觉告诉他，这种算法还可以进行优化，但以他的学识，想破脑袋也想不出来。最后，小明只能按照这种算法不停推算，等到推算完，他撑着饥肠辘辘的身体去取餐的时候，却发现已经到了打烊的时间了！小明没办法，只能到街上买了一个手抓饼，一边泪流满面的吃着，一边发誓自己一定要学好算法……）

最后的优化

实际上，小明的直觉很准确，可惜他的智商没有直觉那么强大~那么接下来，我们接手他的思路，看看接下来还有什么能优化的地方。
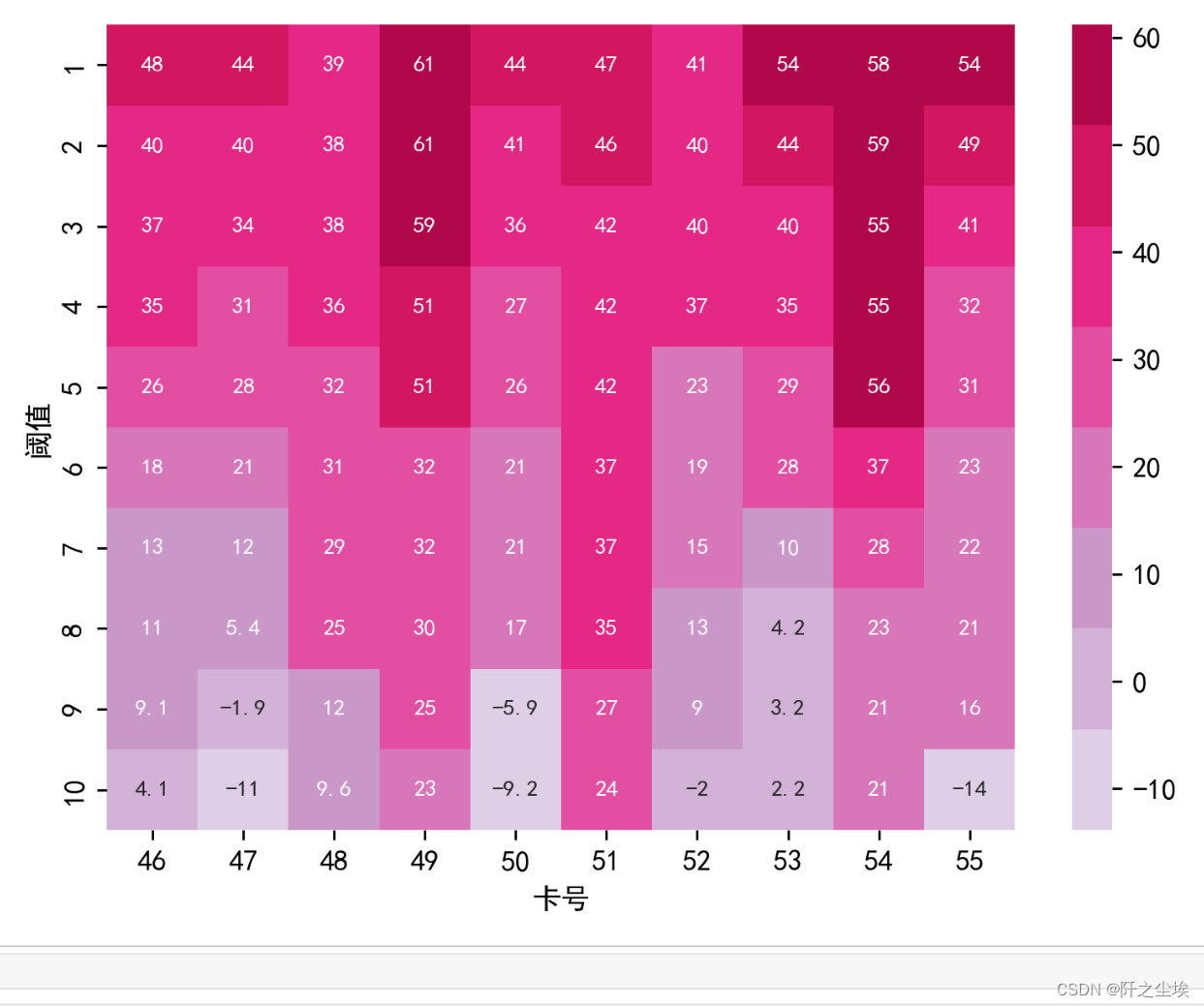
很显然，这次依然可以用滚动数组优化，但为了展示方便，我们先压缩到i和i-1两行：

黄色块是我们当前要确定的值，即f_i,j红色块是根据上面的公式，我们枚举的值，设w[i]=2，则：

接下来是重点，我们看确定f_i,j-2时的表格，黄色块是要确定的值，红色块是枚举的值：

发现了什么？f_i,j-2的值其实就是除了f_i-1,j之外的所有红色块的最大值，那么我们可以通过只比较f_i,j-2和f_i-1,j这两个块的值就可以得出f_i,j的值了，即：
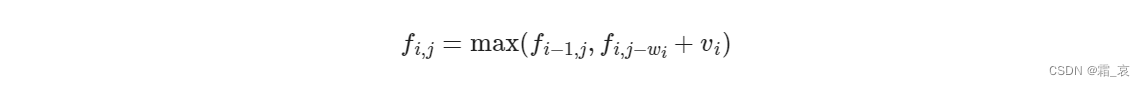
在这里插入图片描述
这就是完全背包问题的转移方程。接下来上代码：

代码

#include <iostream>
using namespace std;
const int maxn = 13010;
int n, W, w[maxn], v[maxn], f[maxn];

int main() {
  cin >> n >> W;
  for (int i = 1; i <= n; i++) cin >> w[i] >> v[i]; 
  for (int i = 1; i <= n; i++)//循环n次，因为要对n件物品进行选择
    for (int l = w[i]; l <= W; l++)//从前向后更新
      f[l] = max(f[l], f[l - w[i]] + v[i]);//转移方程
  cout << f[W];
  return 0;

最后小记以下笔者在写这篇博客时想到的一个关于边界处理的问题：当l<w[i]时，不可能再取第i件物品，所以不会改变数组中的数据；而一开始由于定义的是全局变量，所以数据都初始化为0，也与如果一直不取物品的话，价值为0的事实相符合，所以不特意处理边界是没问题的。
请添加图片描述
我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！码文不易，如果觉得好的话，可以关注一下，我会在将来带来更多更全面的算法讲解！