目录
1. 逻辑运算指令
(1)与 AND
(2)或 OR
(3)非 NOT
(4)异或 XOR
(5)测试 TEST
2. 移位指令
(1)非循环移位
(2)循环移位

1. 逻辑运算指令
(1)与 AND
格式:AND OPRD1,OPRD2
执行:OPRD1 ∧ OPRD2 → OPRD1
功能:实现两个操作数的按位相与。
要求:与加法指令对操作数的要求相同。
AND 指令的执行会影响全部 6 个状态标志位,且 CF = OF = 0。
由于不会产生进位/借位和溢出,所以 CF = OF = 0。又因为 AF 值不定,所以主要是对 ZF、SF、PF 位产生影响。
主要应用
① AND 指令主要用于使目的操作数某些位保持不变而另一些位清 0 。要执行这样的操作就是将要保持不变的位与 “1” 相与,将要清 0 的位与 “0” 相与。
② 使操作数不变,但影响 6 个状态标志位,并使 CF = OF = 0 。例如:AND AX,AX。后续指令会根据需要对状态标志进行判断处理。
MOV 指令不影响 FLAGS,AND 指令能影响 FLAGS。
计算机是不知道操作数是有符号数还是无符号数的,进而不知道操作数的正负。若要运算,一律当作补码来处理。(只有程序员知道操作数的正负)
(2)或 OR
格式:OR OPRD1,OPRD2
执行:OPRD1 ∨ OPRD2 → OPRD1
功能:实现两个操作数的按位相或。
OR 指令的执行会影响全部 6 个状态标志位,且 CF = OF = 0。
主要应用
① OR 指令主要用于使目的操作数某些位保持不变而另一些位置 1 。要执行这样的操作就是将要保持不变的位与 “0” 相或,将要置 1 的位与 “1” 相或。
与置零,或置一。
② 使操作数不变,但影响 6 个状态标志位,并使 CF = OF = 0 。例如:OR AX,AX。
例题
若 AL 中低 7 位为有效数据,最高位留作校验位,初始值为 0,将 AL 中的数据生成偶校验码。

(3)非 NOT
格式:NOT OPRD
执行:OPRD取反 → OPRD
功能:实现一个操作数的按位取反。
NOT 指令的执行不会影响状态标志位。
改变 FLAGS 没有价值,因为我们自己都知道 FLAGS 应该怎么变。
CF = OF = 0,AF 值不定,PF 保持不变,SF 取反。
奇数 + 奇数 = 8,偶数 + 偶数 = 8,故 PF 保持不变。
(4)异或 XOR
格式:XOR OPRD1,OPRD2
执行:OPRD1 ⊕ OPRD2 → OPRD1
功能:实现两个操作数的按位异或。
XOR 指令的执行会影响全部 6 个状态标志位,且 CF = OF = 0。
主要应用
① XOR 指令主要用于使目的操作数某些位保持不变,而另一些位变反。要执行这样的操作就是将要保持不变的位与 “0” 相异或,将要变反的位与 “1” 相异或。
根据异或的定义得到。
② 若两个操作数相同,则结果为 0 。
(5)测试 TEST
格式:TEST OPRD1,OPRD2
执行:OPRD1 ∧ OPRD2
功能:实现两个操作数的按位相与,但结果不送回目的操作数。
TEST 指令执行后两个操作数均不会发生改变。
TEST 指令的执行会影响全部 6 个状态标志位,且 CF = OF = 0。
例题
数据段中从 4000H 开始的单元中有 32 个 8 位的有符号数,要求统计出其中负数的个数并将统计结果保存到 DX 寄存器中。

2. 移位指令
- 目的操作数:通用寄存器、存储器。
- 源操作数:移位次数(1 或 CL)。
(1)非循环移位
① 算术左移 SAL 和逻辑左移 SHL
格式:

执行:

若 1 次移位之后操作数的最高位与 CF 不相同,则 OF = 1,否则 OF = 0。
OF = 1对于 SHL 不表示溢出,对于 SAL 则表示溢出。
Q:我们之前学习算术左移时讲,符号位不变,有效数值左移,这里怎么把符号位移出去了,难道不会导致结果错误吗?
A:算术左移的本质就是将操作数乘 2,而乘 2 的结果是可能产生溢出的。1 次移位之后操作数的最高位与 CF 不相同,则代表移位前有效数值最高位与符号位不相同。这说明有效数值的绝对值已经超过表示范围的一半了,如果再乘 2,那么必定会发生溢出,即结果错误。反之,若移位前有效数值最高位与符号位相同,那么这里移位后的效果仍和我们之前学的一样,因此得到的是一个正确的结果。
② 算术右移 SAR 和逻辑右移 SHR
格式:

执行:

小结
对于逻辑移位指令 SHL 和 SHR,它们将目的操作数视为无符号数。
对于算术移位指令 SAL 和 SAR,它们将目的操作数视为带符号数。当移位次为 n 时,在结果不产生溢出的条件下,其作用分别相当于带符号数乘以 2^n 和除以 2^n 。
例题
设 AX 中存放一个带符号数,若要实现 (AX) × 5 ÷ 2,可由以下几条指令完成,不考虑溢出时。

(2)循环移位
① 不带 CF 的循环移位指令
格式:

执行:

② 带 CF 的循环移位指令
格式:

执行:

注意:目的操作数的最高位/最低位移入 CF,CF 原来的值移入最低位/最高位。
例题1
下面程序段对从数据段存储单元 M 开始的三字数据执行左移一位。

移位指令的共同特点:移出位都会送入 CF 状态位。
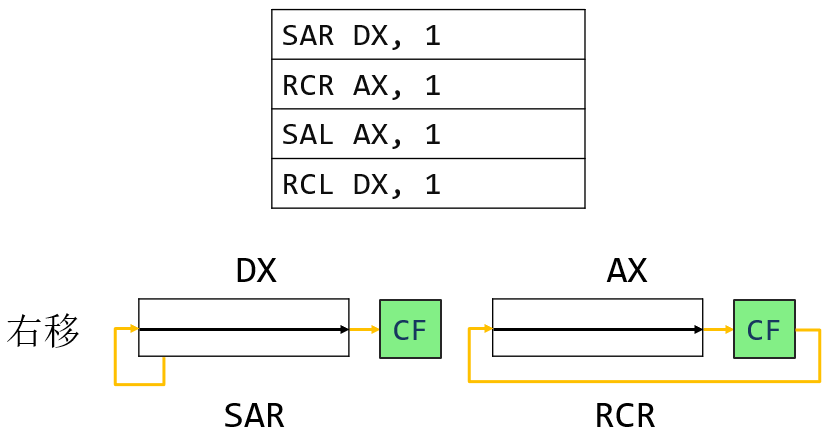
例题2
将 DX 和 AX 两个寄存器组成的 32 位有符号数,其中 AX 为低位部分。先进行 1 位右移操作,然后再进行 1 位左移操作。