ViViT: A Video Vision Transformer
- Abstract
- Overview of vision transformer 回顾ViT
- Embedding video clips 视频编码方式
- Uniform frame sampling 均匀采样
- Tubelet embedding 时空管采样
- 初始化
- 3D卷积代码介绍
- 视频编码输入到模型当中
- Transformer Models for Video
- Spatio-temporal attention 空间-时间注意力
- Factorised encoder
- Factorised self-attention
- Factorised dot-product attention
- 消融实验
Abstract
文章主要transformer在包含时序信息维度的视频格式上的问题展开:
- 视频格式数据生成的token序列数量过多,带来繁重的计算冗余。
- 训练Transfomer结构模型需要引入大规模的数据集,训练对数据条件十分苛刻。
为了高效处理视频数据中生成的大规模时空tokens
①文章提出并探讨了几种对空间和时间维度进行分解的方法,进而提出了相应的网络结构,从而增加模型对视频数据特征提取的效率和可扩展性。
②其次,规范了模型的训练(主要针对模型的训练策略)。目的在小数据集上也能使得Transformer类模型能有很好的效果
Overview of vision transformer 回顾ViT
基础的ViT模型主要有三个模块组成
- Linear Project of Flattened Patches即为Embedding层,对输入的三通道图像数据利用conv卷积层进行分块并完成对应的线性映射,如上式当中的E,而后通过torch.view()进行展平压缩维度。拼接上类别token后采用矩阵相加方式引入位置编码。
- Transformer Encoder模块,对Embedding层输出的token进行多头注意力计算和多层感知机(中间包含Layer Norm)。其中MSA是整个模型的核心部分。
- MLP Head层,堆叠的Transformer Block最终的输出经过Head结构提取出类别token所对应的结果信息,文中通过两个线形层叠加中间插入一个tanh激活函数来实现。
Embedding video clips 视频编码方式
一个视频V有4个维度,T * H * W * C。 变成一个序列token就是 Nt * Nh * Nw * d。加上位置编码, 变成transformer的输入 N * d。
区别于常规的二维图像数据,视频数据相当于需在三维空间内进行采样(拓展了一个时间维度)。而文章中所提出的两钟视频嵌入方法目的都是将视频数据 V ∈ R T × H × W × C \mathrm{~V~}\in\mathbb{R}^{\mathrm{T}\times\mathrm{H}\times\mathrm{W}\times\mathrm{C}} V ∈RT×H×W×C映射到token当中得到 z ~ ∈ R n t × n h × n w × d \tilde{\mathrm{z}}\in\mathbb{R}^{\mathrm{n_t}\times\mathrm{n_h}\times\mathrm{n}_{\mathrm{w}}\times\mathrm{d}} z~∈Rnt×nh×nw×d,而后添加位置编码并对token进行reshape得到最终Transformer的输入 z ∈ R N × d \mathrm{z}\in\mathbb{R}^{\mathrm{N}\times\mathrm{d}} z∈RN×d
Uniform frame sampling 均匀采样
就是先提取帧,然后每一帧按照ViT的方法提取token,然后把不同帧的token拼接起来作为输入
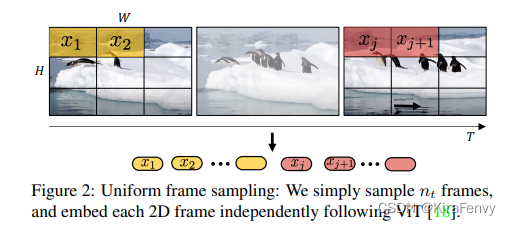
采用相同的采样帧率,从视频数据当中均匀采样
n
t
n_t
nt 帧,使用相同的embedding方法独立地处理每一个帧当中的patch,而后将得到的所有token拼接concat在一起。具体而言,从每个采样获得的帧当中划分
个不重叠的图像块patch,则共产生
n
w
×
n
t
n_w\times{n_t}
nw×nt个不重叠的图像块patch,则共产生
n
t
×
n
w
×
n
t
n_t\times{n_w}\times{n_t}
nt×nw×nt 个tokens输入Transformer当中。
然而这种切片方法对于长时间序列的数据来说生成的token长度极大,并且不同帧间首位相连的patch在位置编码上与真实情况不一致。
Tubelet embedding 时空管采样
前一种方法是提取2D图像特征,这种方法是提取立方体,假设每个tublet的shape是t, w, h,那就是说没t帧提取一次特征,取每一帧相同位置的w, hpatch组成输入
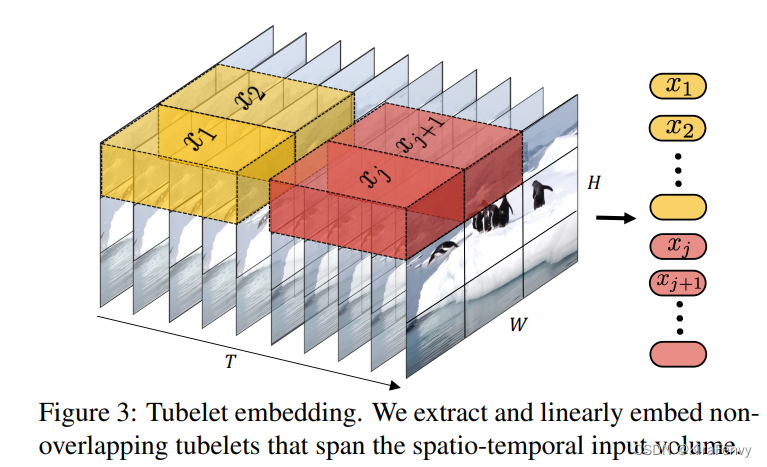
从输入volume(体积)当中提取时空上不重叠的“tubes”,这种方法是将vit嵌入到3D的拓展,embedding层就对应的选取三维卷积。则对于维度为
t
×
h
×
w
t×h×w
t×h×w的tube管来说,
n
t
=
[
T
t
]
,
n
h
=
[
H
h
]
,
n
w
=
[
W
w
]
\mathrm{n_{t}}=[\frac{T}{t}],n_{\mathrm{h}}=[\frac{H}{\mathrm{h}}],n_{\mathrm{w}}=[\frac{W}{\mathrm{w}}]
nt=[tT],nh=[hH],nw=[wW]这种采样方法直接在采样的过程当中就融合了时空信息。
提取不重叠,空间-时间的tubes(立方体)。这个tublelt的维度就是: t * h * w。token就包含了时间、宽、高。
所有的模型都是32帧输入的。
看了下vivit_base_k400的config, 模型名:ViViT- B/16*2。其实16 * 16还是ViT一样的方法。
config.dataset_configs.num_frames = 32 # 采取32帧
config.dataset_configs.stride = 2 #2帧为1个
config.dataset_configs.crop_size = 224 # 大小224
config.model.temporal_encoding_config.method = '3d_conv'
config.model.patches.size = [16, 16, 2] # H,W是 16* 16的
初始化
模型是以Vit为基础进行训练的,所以初始化需要进行特殊处理
Position emb: 复制t份出来,来适应多帧的处理
Embedding emb:
2d的输入没什么好说的
对于3d的输入,提供了两种不同的方式
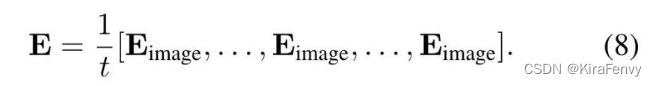
下面的公式可以实现在初始的情况下,等价于只用的1帧的情况,参数由模型自己去学习
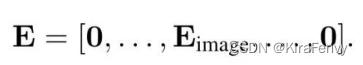
3D卷积代码介绍
首先2D的卷机是一个平面的卷机(H * W), 就是一个H * W的平面 和一个 H * W的卷机核,对应点相乘,输出一个值。
那么3D的卷机就是一个立方体(H * W * D), 就是一个立方体和一个立方体的卷机核相乘,输出一个值。
用pytorch的官方的Conv3D来看, 这个卷机核就是一个3D的立方体 3 * 5 * 2
输入是 (Batch, Channel, Depth, Height, Width) -> (20, 16, 10, 50, 100)
m = nn.Conv3d(16, 33, (3, 5, 2), stride=(2, 1, 1), padding=(4, 2, 0))
input = torch.randn(20, 16, 10, 50, 100)
output = m(input)
output.shape # torch.Size([20, 33, 8, 50, 99]
更改为paper中的输入:
输入是一个batch:16, 3 * 224 * 224的图片, 一共有32帧,
使用kenel,2 * 16 * 16, 理解为2帧变1帧, 图像上 16 * 16的不重叠区域
m = nn.Conv3d(3, 1, (2, 16, 16), stride=(2, 16, 16))
input = torch.randn(16, 3, 32, 224, 224)
output = m(input)
output.shape # torch.Size([16, 1, 16, 14, 14])
视频编码输入到模型当中
输入视频,均匀采样, 知道采样的帧数(n_sampled_frames), 去算间隔, 采样,输出。
def sample_frames_uniformly(x: jnp.ndarray,
n_sampled_frames: int) -> jnp.ndarray:
"""Sample frames from the input video."""
if x.ndim != 5:
raise ValueError('Input shape should be [bs, t, h, w, c].')
num_frames = x.shape[1]
if n_sampled_frames < num_frames:
t_start_idx = num_frames / (n_sampled_frames + 1)
t_step = t_start_idx
else:
t_start_idx = 0
t_step = 1
t_end_idx = num_frames
temporal_indices = jnp.arange(t_start_idx, t_end_idx, t_step)
temporal_indices = jnp.round(temporal_indices).astype(jnp.int32)
temporal_indices = jnp.minimum(temporal_indices, num_frames - 1)
return x[:, temporal_indices] # [n, t_s, in_h, in_w, c]
编码后,从batch, time,h, w, c -> batch, thw, c
def temporal_encode(x,
temporal_encoding_config,
patches,
hidden_size,
return_1d=True,
name='embedding'):
"""Encode video for feeding into ViT."""
n, _, in_h, in_w, c = x.shape
if temporal_encoding_config.method == 'temporal_sampling':
n_sampled_frames = temporal_encoding_config.n_sampled_frames
x = video_utils.sample_frames_uniformly(x, n_sampled_frames)
t_s = x.shape[1]
x = jnp.reshape(x, [n, t_s * in_h, in_w, c])
x = embed_2d_patch(x, patches, hidden_size)
temporal_dims = t_s
if return_1d:
n, th, w, c = x.shape
x = jnp.reshape(x, [n, th * w, c])
else:
n, th, w, c = x.shape
x = jnp.reshape(x, [n, t_s, -1, w, c])
elif temporal_encoding_config.method == '3d_conv':
kernel_init_method = temporal_encoding_config.get('kernel_init_method',
None)
x = embed_3d_patch(x, patches, hidden_size, kernel_init_method, name)
temporal_dims = x.shape[1]
if return_1d:
n, t, h, w, c = x.shape
x = jnp.reshape(x, [n, t * h * w, c])
else:
raise AssertionError('Unknown temporal encoding method.')
assert x.size > 0, ('Found zero tokens after temporal encoding. '
'Perhaps one of the patch sizes is such that '
'floor(dim_size / patch_size) = 0?')
return x, temporal_dims
Transformer Models for Video
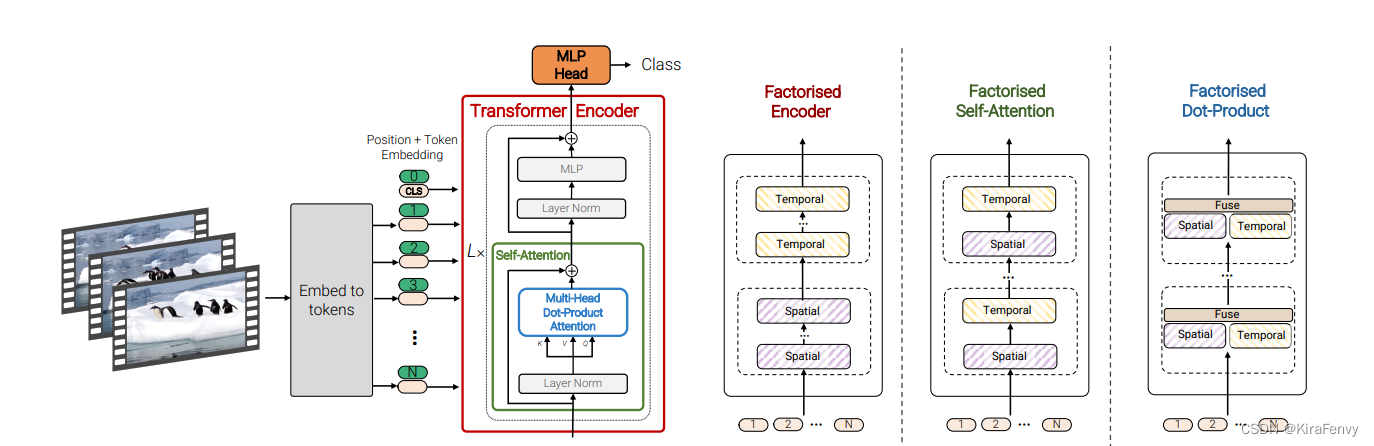
Spatio-temporal attention 空间-时间注意力
伴随着采样的输入帧数增加,token的数量也会线性增加。运算量会平方倍的增加,所以需要更加有效的结构。
这种模型简单地将所有的tokens(包括时空)简单地通过Transformer encoder层,导致问题就是引入指数增长的计算量,每个Transformer层对所有时空token均进行成对交互,这种方式极其低效,具体模型构成方式与另一篇文章:Video Transformer Net 所提出的结构类似,如图4所示

Factorised encoder
使用两个 transformer
- 第一个是 spatial transformer,输入是某一帧的多个token,输出一个token
- 第二个是temporal transformer,输入是前一步多帧的token(每帧对应一个token),输出结果就通过mlp进行分类
模型是2个单独的transformer encoder组成的:
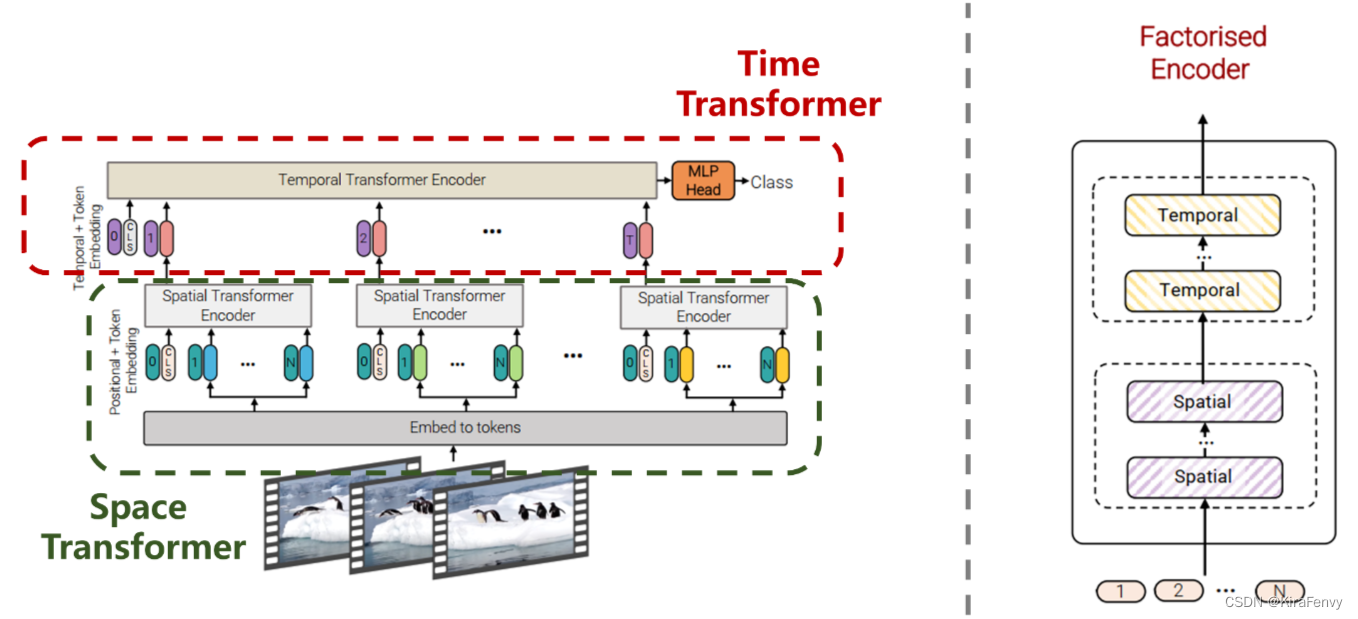
- 空间编码器,通过对同一时间索引的token建模。输出cls_token。
- 这个帧维度的表征,连接在一起,输入时间编码器中。这个输出就是最后的结果。
Factorised encoder方法:构建两个单独的transformer encoder,分别针对空间和时间处理。首先利用空间编码器(Space Transformer),通过对同一时间索引的token建模。输出cls_token。而后将**输出的类别token和帧维度的表征token拼接输入到时间编码器(Time Transformer)**中得到最终的结果,模型结构如图5所示(相当于两个Transformer模型的叠加),实现代码如下:
class ViViT(nn.Module):
def __init__(self, image_size, patch_size, num_classes, num_frames, dim = 192, depth = 4, heads = 3, pool = 'cls', in_channels = 3, dim_head = 64, dropout = 0.,
emb_dropout = 0., scale_dim = 4, ):
super().__init__()
assert pool in {'cls', 'mean'}, 'pool type must be either cls (cls token) or mean (mean pooling)
assert image_size % patch_size == 0, 'Image dimensions must be divisible by the patch size.'
num_patches = (image_size // patch_size) ** 2
patch_dim = in_channels * patch_size ** 2
self.to_patch_embedding = nn.Sequential(
Rearrange('b t c (h p1) (w p2) -> b t (h w) (p1 p2 c)', p1 = patch_size, p2 = patch_size),
nn.Linear(patch_dim, dim),
)
self.pos_embedding = nn.Parameter(torch.randn(1, num_frames, num_patches + 1, dim))
self.space_token = nn.Parameter(torch.randn(1, 1, dim))
self.space_transformer = Transformer(dim, depth, heads, dim_head, dim*scale_dim, dropout)
self.temporal_token = nn.Parameter(torch.randn(1, 1, dim))
self.temporal_transformer = Transformer(dim, depth, heads, dim_head, dim*scale_dim, dropout)
self.dropout = nn.Dropout(emb_dropout)
self.pool = pool
self.mlp_head = nn.Sequential(
nn.LayerNorm(dim),
nn.Linear(dim, num_classes)
)
def forward(self, x):
x = self.to_patch_embedding(x)
b, t, n, _ = x.shape
cls_space_tokens = repeat(self.space_token, '() n d -> b t n d', b = b, t=t)
x = torch.cat((cls_space_tokens, x), dim=2)
x += self.pos_embedding[:, :, :(n + 1)]
x = self.dropout(x)
x = rearrange(x, 'b t n d -> (b t) n d')
x = self.space_transformer(x)
x = rearrange(x[:, 0], '(b t) ... -> b t ...', b=b)
cls_temporal_tokens = repeat(self.temporal_token, '() n d -> b n d', b=b)
x = torch.cat((cls_temporal_tokens, x), dim=1)
x = self.temporal_transformer(x)
x = x.mean(dim = 1) if self.pool == 'mean' else x[:, 0]
return self.mlp_head(x)
Factorised self-attention
通过 self-attention 层将时空数据分开处理
- 空间层只在同一帧内不同token间进行attention操作
- 时间层对不同帧同一位置的token进行attention操作
- 先计算空间自注意力(token中有相同的时间索引),再计算时间的自注意力(token中有相同的空间索引),其实先后顺序无所谓,只要串行就行
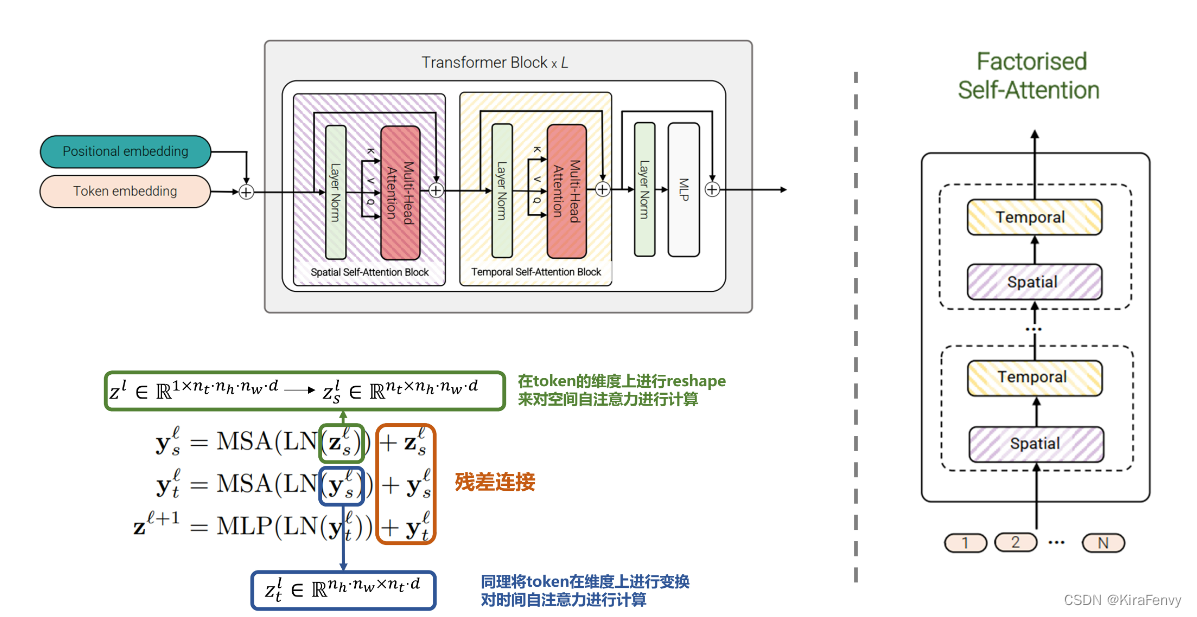
相较于Model 1,这个模型包含相同数量的Transformer层。而此模型思路不是在第 l l l 层计算所有成对的token z l z ^l zl 的多头自注意力,而是将自注意力计算在空间和时间上分解,首先只计算空间上的自注意力(对于相同时间索引的token),而后再进行时间上的计算(对于相同的空间索引)。在降低计算复杂度的同时在每个Transformer层均完成了时空层面的自注意力交互。其结构如图6所示。
自注意力计算:
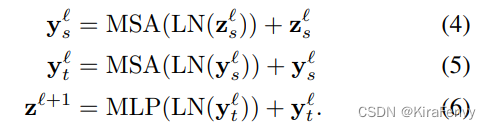
先时间后空间,或者先空间后时间没有区别

def _reshape_to_time_space(x, temporal_dims):
if x.ndim == 3:
b, thw, d = x.shape
assert thw % temporal_dims == 0
hw = thw // temporal_dims
x = jnp.reshape(x, [b, temporal_dims, hw, d])
assert x.ndim == 4
return x、
reshape_to_2d_factorized, 就是将batch, h * w, channel -> batch, w, h, channel
def reshape_to_2d_factorized(x: jnp.ndarray, axis: int,
two_d_shape: Tuple[int, int, int, int]):
"""Converts 1d inputs back to 2d after axial attention."""
assert x.ndim == 3, ('The input dimention should be '
'[batch_size, height*width, channel]')
batch_size, height, width, channel = two_d_shape
if axis == 1:
assert x.shape[0] == batch_size * width
return x.reshape((batch_size, width, height, channel)).transpose(
(0, 2, 1, 3))
elif axis == 2:
assert x.shape[0] == batch_size * height
return x.reshape(two_d_shape
def reshape_to_2d_factorized(x: jnp.ndarray, axis: int,
two_d_shape: Tuple[int, int, int, int]):
"""Converts 1d inputs back to 2d after axial attention."""
assert x.ndim == 3, ('The input dimention should be '
'[batch_size, height*width, channel]')
batch_size, height, width, channel = two_d_shape
if axis == 1:
assert x.shape[0] == batch_size * width
return x.reshape((batch_size, width, height, channel)).transpose(
(0, 2, 1, 3))
elif axis == 2:
assert x.shape[0] == batch_size * height
return x.reshape(two_d_shape)
在不同的维度上做注意力,来实现时间和空间。
其实也是一样的,LN + atttion + 残差连
def _run_attention_on_axis(inputs, axis, two_d_shape):
"""Reshapes the input and run attention on the given axis."""
inputs = model_utils.reshape_to_1d_factorized(inputs, axis=axis)
x = nn.LayerNorm(
dtype=self.dtype, name='LayerNorm_{}'.format(_AXIS_TO_NAME[axis]))(
inputs)
x = self_attention(
name='MultiHeadDotProductAttention_{}'.format(_AXIS_TO_NAME[axis]))(
x, deterministic=deterministic)
x = nn.Dropout(rate=self.dropout_rate)(x, deterministic)
x = x + inputs
return model_utils.reshape_to_2d_factorized(
x, axis=axis, two_d_shape=two_d_shape)
整个这个因式分解的注意力模块,就是在不同的轴上,做自注意力。
可以使用先时间后空间,attention_axes = (1, 2)。或者先空间后时间,attention_axes= (2, 1)。
所以整个就是: 时间attn + 空间attn + LN + MLP
Factorised dot-product attention
时间、空间heads是并行的,而不是串行的。
spatial还是同一帧内不同token,temporal是不同帧同一位置的token
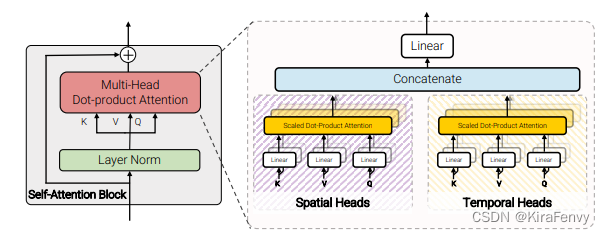
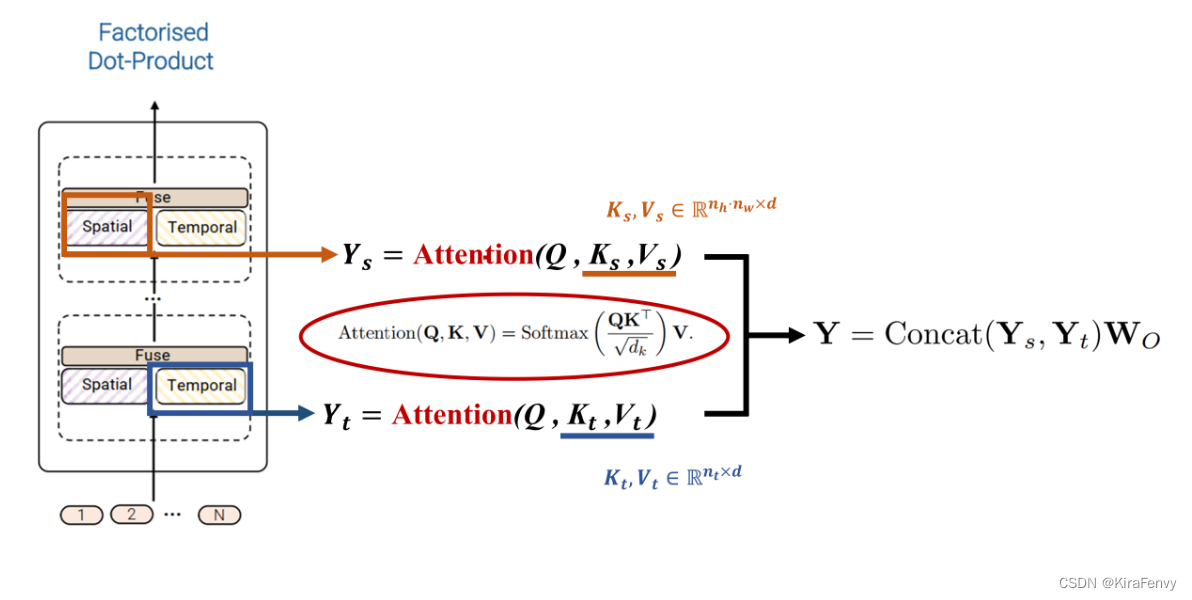
第四种模型的思想则是通过利用dot-product点积注意力操作来取代上述的因式分解factorisation操作,通过注意力计算的方式来代替简单的张量reshape。思想是对于空间注意力和时间注意力分别构建对应的键、值。具体思路如图所示。
class FDATransformerEncoder(nn.Module):
"""Factorized Dot-product Attention Transformer Encoder"""
def __init__(self, dim, depth, heads, dim_head, mlp_dim, nt, nh, nw, dropout=0.):
super().__init__()
self.layers = nn.ModuleList([])
self.nt = nt
self.nh = nh
self.nw = nw
for _ in range(depth):
self.layers.append(
PreNorm(dim, FDAttention(dim, nt, nh, nw, heads=heads, dim_head=dim_head, dropout=dropout)))
def forward(self, x):
for attn in self.layers:
x = attn(x) + x
return x
class FDAttention(nn.Module):
"""Factorized Dot-product Attention"""
def __init__(self, dim, nt, nh, nw, heads=8, dim_head=64, dropout=0.):
super().__init__()
inner_dim = dim_head * heads
project_out = not (heads == 1 and dim_head == dim)
self.nt = nt
self.nh = nh
self.nw = nw
self.heads = heads
self.scale = dim_head ** -0.5
self.attend = nn.Softmax(dim=-1)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
self.to_out = nn.Sequential(
nn.Linear(inner_dim, dim),
nn.Dropout(dropout)
) if project_out else nn.Identity()
def forward(self, x):
b, n, d, h = *x.shape, self.heads
qkv = self.to_qkv(x).chunk(3, dim=-1)
q, k, v = map(lambda t: rearrange(t, 'b n (h d) -> b h n d', h=h), qkv)
qs, qt = q.chunk(2, dim=1)
ks, kt = k.chunk(2, dim=1)
vs, vt = v.chunk(2, dim=1)
# Attention over spatial dimension
qs = qs.view(b, h // 2, self.nt, self.nh * self.nw, -1)
ks, vs = ks.view(b, h // 2, self.nt, self.nh * self.nw, -1), vs.view(b, h // 2, self.nt, self.nh * self.nw, -1)
spatial_dots = einsum('b h t i d, b h t j d -> b h t i j', qs, ks) * self.scale
sp_attn = self.attend(spatial_dots)
spatial_out = einsum('b h t i j, b h t j d -> b h t i d', sp_attn, vs)
# Attention over temporal dimension
qt = qt.view(b, h // 2, self.nh * self.nw, self.nt, -1)
kt, vt = kt.view(b, h // 2, self.nh * self.nw, self.nt, -1), vt.view(b, h // 2, self.nh * self.nw, self.nt, -1)
temporal_dots = einsum('b h s i d, b h s j d -> b h s i j', qt, kt) * self.scale
temporal_attn = self.attend(temporal_dots)
temporal_out = einsum('b h s i j, b h s j d -> b h s i d', temporal_attn, vt)
消融实验
比较不同的token获取方式
比较了不同变种的transformer
比较了多种数据增强方式
比较了不同输入数据尺寸
比较了几类变种
比较了不同的输入帧数