先进行一些定义，假设目前有一个无向连通图

割点：某点及其边去掉后，图不再连通

桥：某条边去掉后，图不再联通

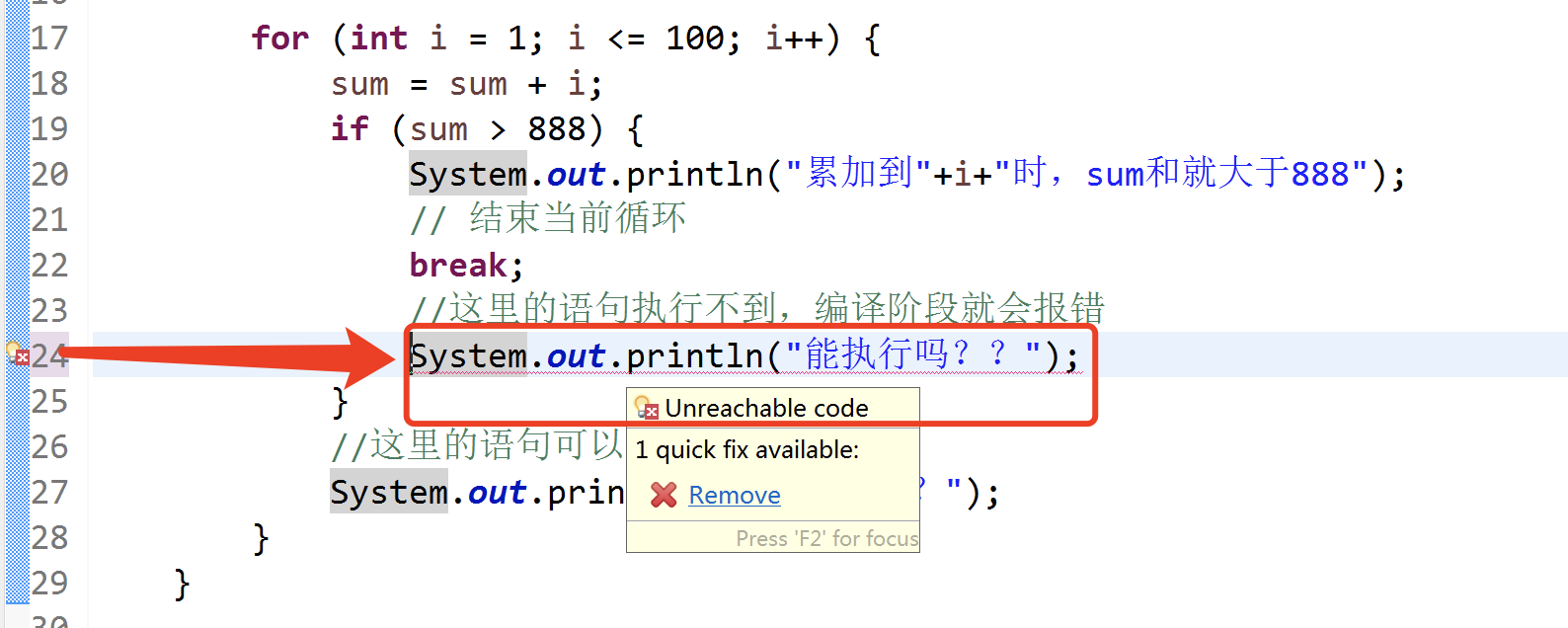
tarjan算法求割点

不考虑子结点到父结点的情况

dfn(x) x实际杯访问的时间点

low(x) x通过图可回溯到的最早时间点

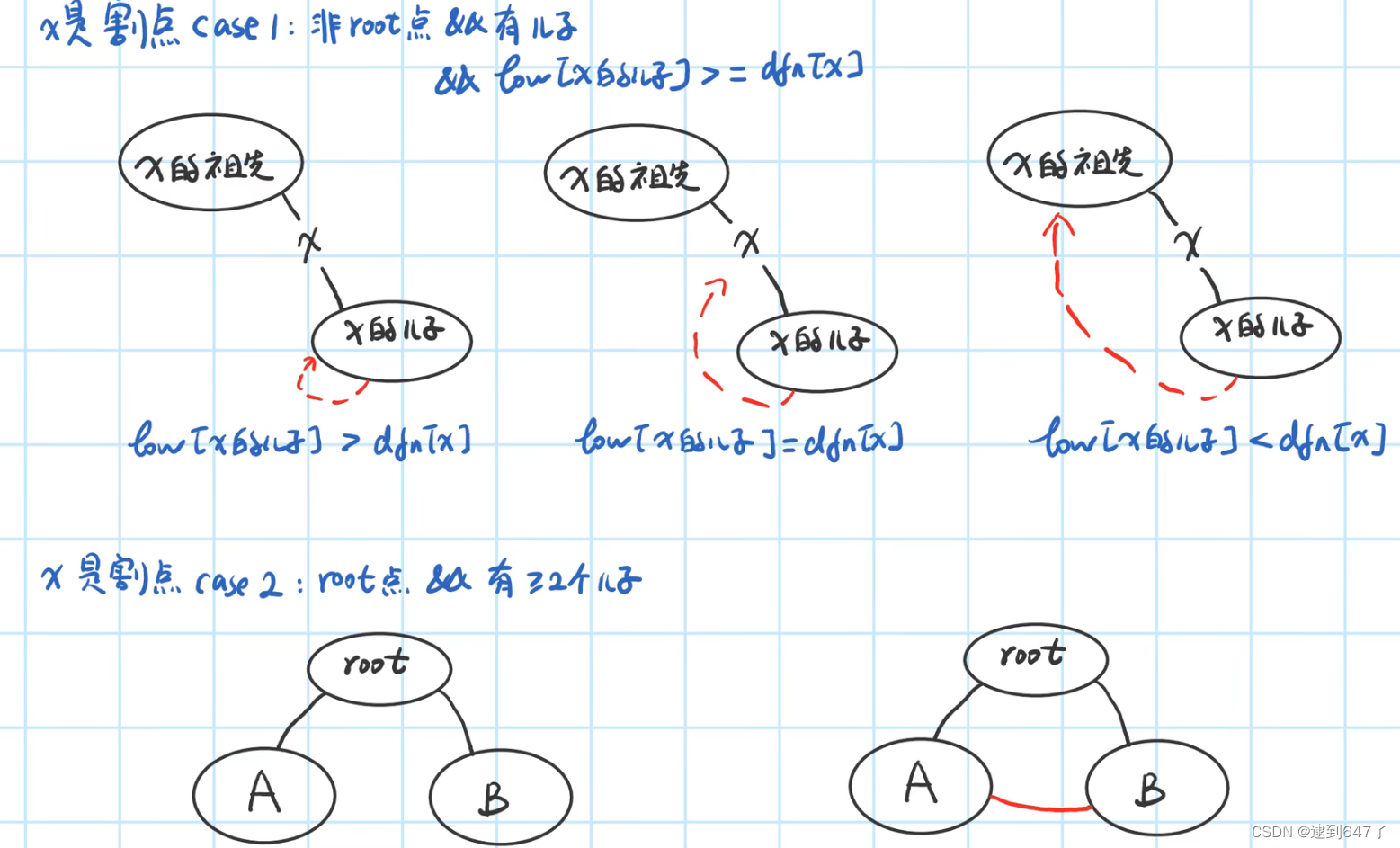
 在CASE1 中，左中情况为割点，右情况不是割点

在CASE2 中， 两种情况为割点

tarjan算法求桥

 

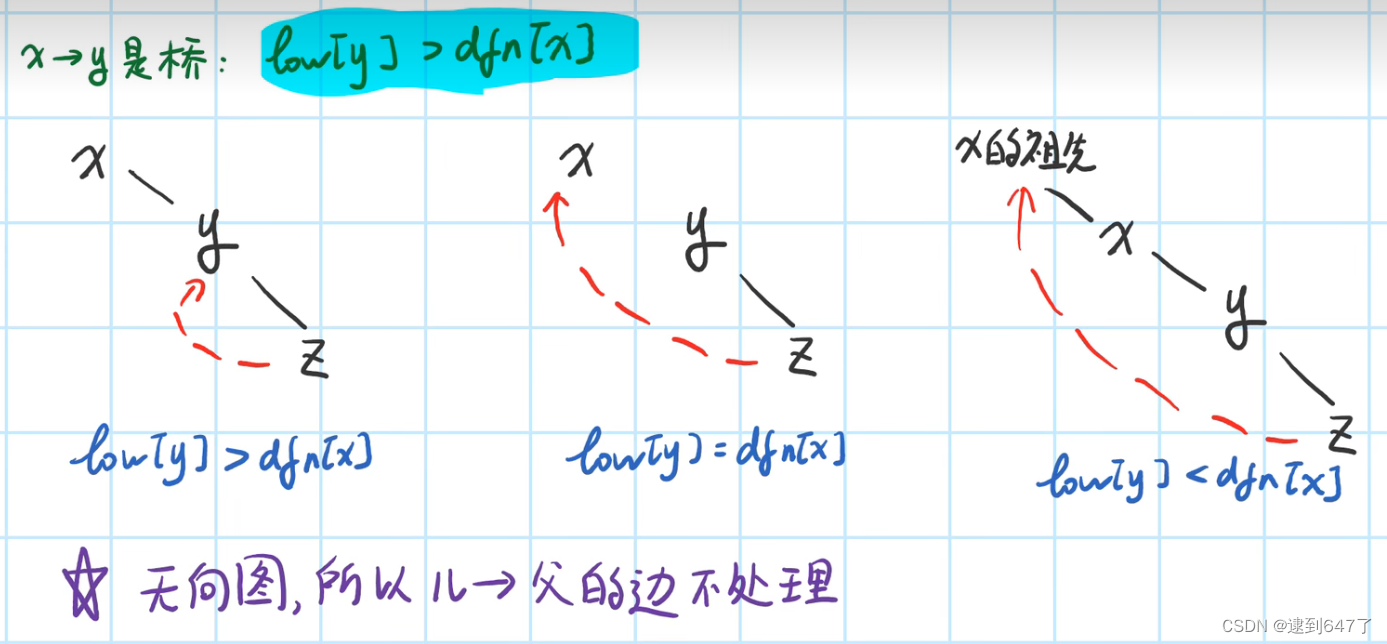
直接上实战：

1192. 查找集群内的关键连接 - 力扣（LeetCode）https://leetcode.cn/problems/critical-connections-in-a-network/

class Solution {
public:
    vector<int> dfn;
    vector<int> low;
    vector<int> fa;
    vector<vector<int>> res;

    void tarjan(int x , vector<vector<int>> &g , int times){
        dfn[x] = times;
        low[x] = times;
        ++times;
        int child = 0;
        for(auto y : g[x]){
            if(!dfn[y]){
                child++;
                fa[y] = x;
                tarjan(y , g , times);
                if(low[y]>dfn[x])res.push_back({x,y});
                low[x] = min(low[x] , low[y]);
            }
            else{
                if(y!=fa[x])low[x] = min(low[x] , dfn[y]);
            }
        }
    }

    vector<vector<int>> criticalConnections(int n, vector<vector<int>>& connections) {
        vector<vector<int>> g(n);
        for(auto cur : connections){
            g[cur[0]].push_back(cur[1]);
            g[cur[1]].push_back(cur[0]);
        }

        dfn.resize(n , 0);
        low.resize(n , 0);
        fa.resize(n , -1);
        int times = 1;
        for(int i = 0 ; i<n ; i++){
            if(dfn[i]==0){
                tarjan(i , g , times);
            }
        }
        return res;
    }
};

每个点都对应一组数据[dfn , low]

 这里注意，在y点为访问过的判断里面，low[x] 应该等于 min(low[x] , dfn[y])，搬运别人的解释：如果是一个八字形的话，y能到通过x到达x的父结点或者祖先结点，如果y需要通过x到达low[x]，x是割点，不满足条件。

参考算法视频（讲得挺好的~）：

[算法]轻松掌握tarjan割点&桥算法_5_code实现_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1GE411G7Kq/?spm_id_from=333.999.0.0&vd_source=bcaf3fd41fa79919325be693534a978d