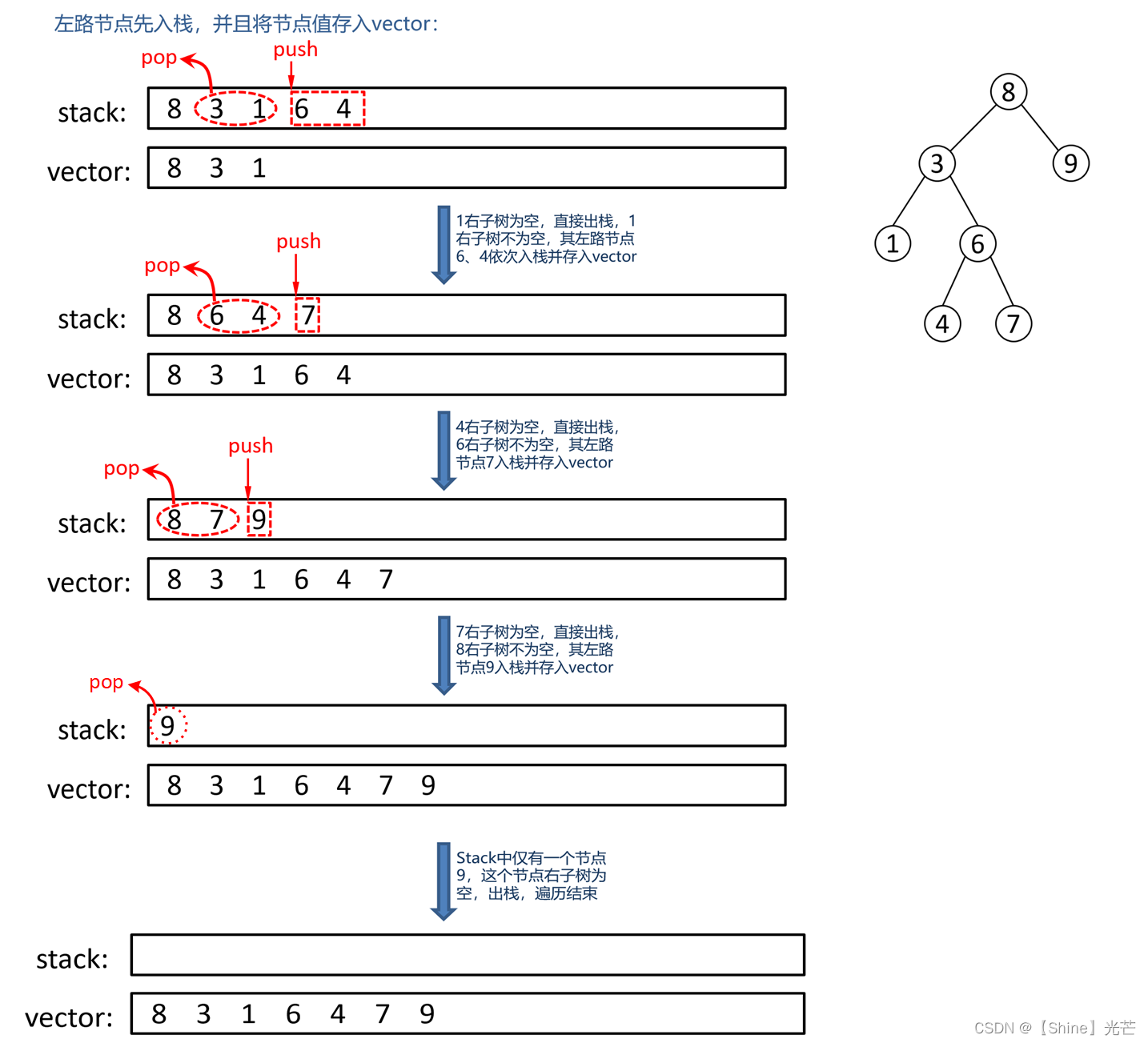
1.哈夫曼树的背景

        哈夫曼（霍夫曼、赫夫曼）David Albert Huffman(August9,1925-October7,1999)。计算机科学的先驱，以他的哈夫曼编码闻名，在他的一生中，对于有限状态自动机，开关电路，异步过程和信号设计有杰出的贡献。

        他发明的Huffman编码能够使我们通常的数据传输数量减少到最小。这个编码的发明和这个算法一样十分引人入胜。1950年，Huffman在MlT的信息理论与编码研究生班学习。Robert Fano教授让学生们自己决定是参加期末考试还是做一个大作业。而Huffmani选择了后者，原因很简单，因为解决一个大作业可能比期未考试更容易通过。这个大作业促使了Huffman算法的诞生。

        离开MIT后，Huffman来到Jniversity of California的计算机系任教，并为此系的学术付了许多杰出的工作。而他的算法也广泛应用于传真机，图象压缩和计算机安全领域。但是Huffman却从未为此算法申请过专利或其它相关能够为他带来经济利益的东西，他将他全部的精力放在教学上，以他自己的话来说，"我所要带来的就是我的学生。“

 

 看一眼就知道，这是大师无疑啦

2.哈夫曼树的基本概念

先引入例题：

编程：将学生的百分制成绩转换为五分制成绩

<60 : E

60~69 : D

70~79 : C

80~89 : B

90~100 : A

以往我们可以使用if-else语句嵌套或者switch分支语句实现

if(score < 60)
    grade = 'E';
else if(score < 70)
    grade = 'D';
else if(score < 80)
    grade = 'C';
else if(score < 90)
    grade = 'B';
else
    grade = 'A';

 

应用哈夫曼树的概念

假设学生的成绩数据共10000个：

则5%的数据需1次比较，15%的数据需2次比较，40%的数据需3次比较，40%的数据需4次比较，因此10000个数据比较的次数为：10000(1×5%+2×15%+3×40%+4×10%)=31500次

但是用哈夫曼树来比较：

 

 哈夫曼树所以又叫最优二叉树

路径：从树中一个结点到另一个结点之间的分支构成这两个结点间的路径。

结点的路径长度：两结点间路径上的分支数。

 

 树的路径长度：从树根到每一个结点的路径长度之和。记作：TL

上面题目的路径之和：0+1+1+2+2+3+3+4+4 = 20

结点数目相同的二叉树中，完全二叉树是路径长度最短的二叉树。

权(weight)：将树中结点赋给一个有着某种含义的数值，则这个数值称为该结点的权。

结点的带权路径长度：从根结点到该结点之间的路径长度与该结点的权的乘积。

树的带权路径长度：树中所有叶子结点的带权路径长度之和。

记作：

Weighted Path Length

例：有4个结点a,b,G,d,权值分别为7,5,2,4，

构造以此4个结点为叶子结点的二叉树：

 

 WL = 2 * 7 + 2 * 5 + 2 * 2 + 2 * 4 = 36

 

 WL = 2 * 1 + 4 * 2 + 7 * 3 + 5 * 3 = 46

哈夫曼树：最优树

带权路径长度(WPL)最短的树

“带权路径长度最短”是在“度相同”的树中比较而得的结果，因此有最优二叉树、最优三叉树之称等等。

因为构造这种树的算法是由哈夫曼教授于1952年提出的，所以被称为哈夫曼树，相应的算法称为哈夫曼算法。

3.哈夫曼树的构造算法

哈夫曼树中权越大的叶子离根越近

贪心算法：构造哈夫曼树时首先选择权值小的叶子结点

哈夫曼算法（构造哈夫曼树的方法）

1. 根据石>给定的权值{w,%,w}构成2棵二叉树的森林

   F={T1,T2,...,Tn},其中T只有一个带权为wi的根结点。

构造森林全是根

1. 在F中选取两棵根结点的权值最小的树作为左右子树，构造一棵新的 二叉树，且设置新的二叉树的根结点的权值为其左右子树上根结点的权值 之和。

选用两小造新树

1. 在F中删除这两棵树，同时将新得到的二叉树加入森林中。

删除两小添新人

1. 重复步骤2和3，直到森林中只有一棵树为止，这棵树即为哈夫曼树

哈夫曼算法口诀：

1、构造森林全是根；

2、选用两小造新树；

3、删除两小添新人；

4、重复2、3剩单根。

 

 Attention：

1. 哈夫曼树的结点的度数为0或2，没有度为1的结点。

2. 包含n个叶子结点的哈夫曼树中共有2n - 1个结点。

例题：

 

 

 总结：

1. 在哈夫曼算法中，初始时有n棵二叉树，要经过n - 1次合并最终形成哈夫曼树。

2. 经过n - 1次合并产生n - 1个新结点，且这n - 1个新节点都是具有两个孩子的分支结点。

3. 可见：哈夫曼树中共有2n - 1个结点，且其所有分支结点的度均不为1。

4.哈夫曼树构造算法的实现

1.采用顺序存储结构（一维结构数组）

结点类型定义

typedef struct
{
    int weight;
    int parent, lch, rch;
}HTNode,*HuffmanTree;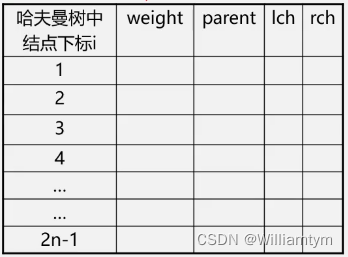

 

 哈夫曼树中共有2n-1个结点，不用0下标，数组大小为2n。

哈夫曼树构造算法

1. 初始化HT[1.....2n-1]：lch = rch = parent = 0;

void CreateHuffmanTree(HuffmanTree HT, int n)
{
    //构造哈夫曼树——哈夫曼算法
    if(n <= 1) return;
    m = 2 * n - 1;//数组共2*n-1个元素
    HT = new HTNode[m + 1];//0号单元没有使用，HT[m]表示根节点
    for(int i = 1;i <= m; ++i)//将2n-1个元素的lch、rch、parent置为0
    {
        HT[i].lch = 0;
        HT[i].rch = 0;
        HT[i].parent = 0;
    }
    for(int i = 1;i <= 0; ++i)
    {
        cin >> HT[i].weight;//输入前n个元素的weight值
    }
    //初始化结束，下面开始建立哈夫曼树
}

1. 输入初始n个叶子结点：置HT[1n]的weight值；

2. 进行一下n-1次合并，依次产生n-1个结点HT[i]，i = n+1......2n-1;

   a)在HT[1....i-1]中选两个未被选过（从parent==0的结点中选）的weight最小的两个结点HT[s1]和HT[s2]，s1、s2为两个最小结点下标；

   b)修改HT[s1]和HT[s2]的parent值：HT[s1].parent = i；HT[s2].parent = i;

   c)修改新产生的HT[i]：HT[i].weight = HT[s1].weight + HT[s2].weight;HT[i].lch = s1; HT[i].rch = s2;

续

//续算法
for(int i = n+1;i <= m; i++)//合并产生n-1个结点——构造Huffman树
{
    Select(HT, i-1, s1, s2);//在HT[k](1 ≤ k ≤ i1)中选择其双亲域为0
    //且权值最小的结点，并返回它们在HT中的序号s1和s2
    HT[s1].parent = i;
    HT[s2].parent = i;//表示从F中删除s1，s2
    HT[i].lch = s1;
    HT[i].rch = s2;//s1和s2分别作为i的左右孩子
    HT[i].weight = HT[s1].weight + HT[s2].weight;//i的权值为左右孩子权值之和
}

5.哈夫曼编码

在远程通讯中，要将带传字符转换成由二进制的字符串

设要传送的字符为：ABACCDA

若编码为：A——00 B——01 C——10 D——11

ABACCDA——00010010101100

若将编码设计为长度不等的二进制编码，即让待传字符串中出现次数较多的字符采用尽可能短的编码，则转换的二进制字符串便可能减少。

 

 不能有重码，不然会造成代码歧义。

关键：要设计长度不等的编码，则必须使任一字符的编码都不是另一个字符的编码的前缀

方法：

1. 统计字符集中每个字符在电文中出现的平均概率（概率越大，要求编码越短）；

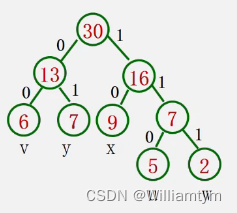
2. 利用哈夫曼树的特点：权值越大的叶子离根越近；将每个字符的概率值作为权值，构造哈夫曼树。则概率越大的结点，路径越短。

3. 在哈夫曼树的每个分支上标上0或1：

   结点的左分支标0，右分支标1

   把从根到每个叶子的路径上的符号连接起来，作为该叶子代表的字符的编码

例题：

 

 两个问题：

1. 为什么哈夫曼编码能够保证是前缀编码？ 因为没有一片树叶是另一片树叶的祖先，所以每个叶结点的编码就不可能是其它叶结点编码的前缀

2. 为什么哈夫曼编码能够保证字符编码总长最短？

   因为哈夫曼树的带权路径长度最短，故字符编码的总长最短。

6.哈夫曼编码的算法实现

void CreateHuffmanCode(HuffmanTree HT, HuffmanCode &HC, int n)
{
    //从叶子结点到根逆向求每个字符的哈夫曼编码，存储在编码表HC中
    HC = new char*[n+1];//分配n个字符编码的头指针矢量
    cd = new char [n];//分配临时存放编码的动态数组空间
    ch[n-1] = '\0';//编码结束符
    for(int i = 1;i <= n; ++i)
    {
        start = n - 1;
        c = i;
        f = HT[i].parent;
        while(f!=0)
        {
            //从叶结点开始向上回溯，直到根节点
            --start;//回溯一次start向前指向的一个位置
            if(HT(f).lchild == c)
                cd[start] = '0';//结点c是f的左孩子，则生成代码0
            else
                cd[start] = '1';//结点c是f的右孩子，则生成代码1
            c = f;
            f = HT[f].parent;//继续向上回溯
        }
        HC[i] = new char[n - start];//为第i个字符编码从临时空间cd复制到HC的当前行中
        strcpy(HC[i], &cd[start]);//将求得的编码从临时空间cd复制到HC的当前行中
    }
    delete cd;//释放临时空间
}//CreateHuffanCode

7.文件的编码和解码

1. 编码： 输入各字符及其权值 构造哈夫曼树一HT[i] 进行哈夫曼编码HC[i] 查HC[i]，得到各字符的哈夫曼编码

2. 解码： 构造哈夫曼树 依次读入二进制码 读入0，则走向左孩子；读入1，则走向右孩子 一旦到达某叶子时，即可译出字符 然后再从根出发继续译码，指导结束

 

 

 构建哈夫曼树HT

求出原码报文OC

 

8.C++代码实现

#define _CRT_SECURE_NO_WARNINGS
#include <map>
#include <cmath>
#include <vector>
#include <iostream>
#include <string>
#include <algorithm>
using namespace std;
 
typedef struct binaryTree {
	int node = -1;
	struct binaryTree* lchild = NULL, * rchild = NULL;
}Tree, * TreePointer;
 
void inputElement();
bool compare(int a, int b);
TreePointer myPopArrEleToTree();
int myPopArr();
TreePointer myPopMap(int iindex);
void createSubTree();
void joinNumToSubTree();
void joinSubTreeToNum();
void joinSubTreeToSubTree();
void xin(TreePointer& T);
 
vector<int> arr;  //用于存储当前所有元素，永远是按绝对值从小到大排序，正常元素为正数，如果是子树为负数  如队列{2,-3 5 -6 7.8} 
map<int, TreePointer> treeMap;  //用于存放子树
 
int main(void) {
	inputElement();
	while (arr.size()>2) {  //运行到最后只剩两个元素，执行后会生成最后一个树，这个树就是我们要的答案
		if (arr.size() >= 2 && arr[0] > 0 && arr[1] > 0)
			createSubTree();
 
		//如果两个元素是，一个子树，一个数字
		if (arr.size() >= 2 && arr[0] < 0 && arr[1]>0)
			joinSubTreeToNum();
 
		if (arr.size() >= 2 && arr[0] > 0 && arr[1] < 0) 
			joinNumToSubTree();
 
		if (arr.size() >= 2 && arr[0] < 0 && arr[1] < 0) 
			joinSubTreeToSubTree();
	}
	cout << "result: ";
	for (auto t : treeMap) 
		xin(t.second);
	return 0;
}
 
//输入元素，输入-1退出
void inputElement() {
	int in;
	while (1) {
		cin >> in;
		if (in == -1) break;
		arr.push_back(in);
	}
	sort(arr.begin(), arr.end(), compare);
}
 
//比较器
bool compare(int a, int b) {
	return abs(a) < abs(b);
}
 
//获取最小的值并且获取后删除，给树赋值后返回
TreePointer myPopArrEleToTree() {
	TreePointer T = new Tree;
	T->node = arr[0];
	arr.erase(arr.begin());
	return T;
}
 
//过去arr的第一个元素，并且删除第一个元素
int myPopArr() {
	int i = arr[0];
	arr.erase(arr.begin());
	return i;
}
 
//获取treeMap中指定的子树，在treeMap中删除这个子树，并返回这个子树
TreePointer myPopMap(int index) {
	TreePointer T = treeMap[index];
	treeMap.erase(index);
	return T;
}
 
//添加元素
void addToArr(int i) {
	arr.push_back(i);
	sort(arr.begin(), arr.end(), compare);
}
 
//挨着的如果是两个数字则创建一个子树,并放到treeMap中
void createSubTree() {
	TreePointer T = new Tree;
	T->lchild = myPopArrEleToTree();
	T->rchild = myPopArrEleToTree();
	treeMap[-(T->lchild->node + T->rchild->node)] = T;
	addToArr(-(T->lchild->node + T->rchild->node));
}
 
//挨着的如果是一个子树与数字创建一个子树,并放到treeMap中
void joinSubTreeToNum() {
	TreePointer T = new Tree;
	int weight = myPopArr();
	T->lchild = myPopMap(weight);
	T->rchild = myPopArrEleToTree();
	treeMap[-(-weight + T->rchild->node)] = T;
	addToArr(-(-weight + T->rchild->node));
}
 
//挨着的如果是一个数字与子树创建一个子树,并放到treeMap中
void joinNumToSubTree() {
	TreePointer T = new Tree;
	T->rchild = myPopArrEleToTree();
	int weight = myPopArr();
	T->lchild = myPopMap(weight);
	treeMap[-(-weight + T->rchild->node)] = T;
	addToArr(-(-weight + T->rchild->node));
}
 
//挨着的如果是一个子树与子树创建一个子树,并放到treeMap中
void joinSubTreeToSubTree() {
	TreePointer T = new Tree;
	int weight1 = myPopArr(), weight2 = myPopArr();
	T->lchild = myPopMap(weight1);
	T->rchild = myPopMap(weight2);
	treeMap[-(-weight1 + (-weight2))] = T;
	addToArr(-(-weight1 + (-weight2)));
}
 
string str = "";
void xin(TreePointer& T) {
	if (T) {
		if (T->node != -1)
			cout << str << " ";
		str += "0";
		xin(T->lchild);
		str = str.substr(0, str.size() - 1);
		str += "1";
		xin(T->rchild);
		str = str.substr(0, str.size() - 1);
	}
}