目录
一. 前序遍历的非递归实现
二. 中序遍历的非递归实现
三. 后序遍历的非递归实现
一. 前序遍历的非递归实现
我们知道,前序遍历的访问顺序为:根节点 -> 左子树 -> 右子树。如图1.1所示的二叉树,我们要通过非递归实现前序遍历,其思路与递归实现并没有太大差别,可将非递归前序遍历这个大问题拆分为两个小问题:
- 访问左路节点
- 访问左路节点的每个右子树(子问题)
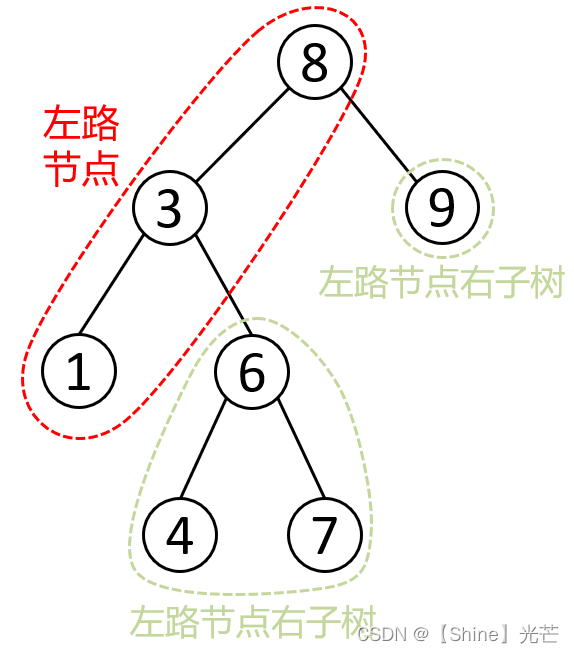
为此,我们需要一个栈做辅助,同时将遍历访问的节点的数据存入一个vector数组中。对于每一颗子树,将其左路节点节点地址入栈并将节点中的数据存入vector中。当左路节点全部入栈之后,取栈顶节点地址,通过top()->right访问右子树,解决下一个子问题。在循环遍历的过程中,我们使用cur记录当前访问的节点的地址,如果cur不为nullptr或栈不为空,那么继续循环,否则遍历结束,终止循环。图1.2以1.1所示的二叉树为例,展示了二叉树前序遍历的非递归实现逻辑。
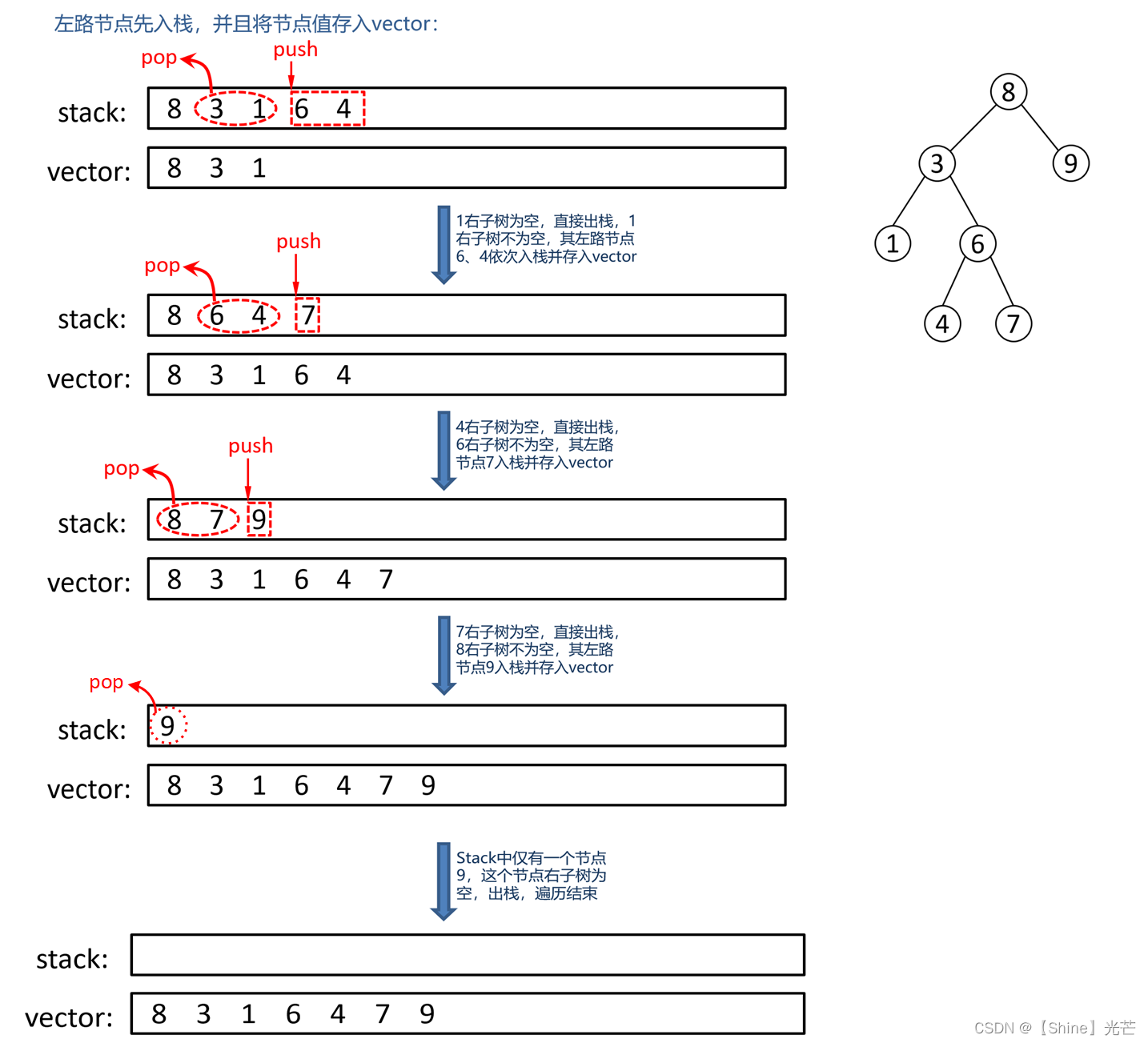
代码段1:(二叉树前序遍历的非递归实现)
template<class T>
struct TreeNode //二叉树节点
{
struct TreeNode* _left;
struct TreeNode* _right;
T _val;
TreeNode(const T& val)
: _left(nullptr)
, _right(nullptr)
, _val(val)
{ }
};
//二叉树前序遍历非递归实现函数
template<class T>
std::vector<T> PrevOrderNonRecursion(TreeNode<T>* root)
{
std::vector<T> v; //存储遍历访问的数据
std::stack<TreeNode<T>*> st; //存储遍历到的节点的地址
TreeNode<T>* cur = root;
while (cur || !st.empty())
{
//1.遍历访问左侧路径的节点
while (cur)
{
st.push(cur);
v.push_back(cur->_val);
cur = cur->_left;
}
//2.获取栈顶节点,解决右子树子问题
TreeNode<T>* top = st.top();
st.pop();
cur = top->_right;
}
return v;
}二. 中序遍历的非递归实现
中序遍历的实现思路与前序遍历类似,主要区别在于:
- 前序遍历是在遍历左树的时候访问节点,并经节点中的数据尾插到vector中。
- 后续遍历是在从栈中删除的点时,将栈顶节点中的数据尾插到vector中。
这样就可以保证每次访问节点之前,保证当前被访问的节点的左子树为空或者左子树中的所有节点都已经被访问。
代码段2:(非递归实现中序遍历)
//二叉树中序遍历非递归实现函数
template<class T>
std::vector<T> InOrderNonRecursion(TreeNode<T>* root)
{
std::vector<T> v;
std::stack<TreeNode<T>*> st;
TreeNode<T>* cur = root;
while (cur || !st.empty())
{
//遍历左侧路径上的节点,依次入栈
while (cur)
{
st.push(cur);
cur = cur->_left;
}
//取出栈顶节点,然后访问,该节点的左子树要么为空,要么已被访问过了
TreeNode<T>* top = st.top();
st.pop();
v.push_back(top->_val);
//解决右子树子问题
cur = top->_right;
}
return v;
}三. 后序遍历的非递归实现
后序遍历的非递归实现也是依靠stack栈这一数据结构来实现的,与前序和中序遍历不同的是,后序遍历由于最后访问根节点,不能在栈顶拿出节点之后,直接访问节点数据存入vector,而是应当保证根节点的左子树和右子树中所有节点都被访问过后,在去访问这个根节点。
为了判断是否对某个栈顶节点进行访问,引入一个新变量prev,记录前一个被访问到的节点,若满足以下两种情况之一,则对该栈顶节点进行访问:
- 该节点的右子节点为nullptr。
- 该节点的右子节点与之前访问的节点prev相同。
如果不满足条件,那么先去访问栈顶节点的右子树,之后再访问这个栈顶节点。
代码段3:(后序遍历的非递归实现)
template<class T>
std::vector<T> PostOrderNonRecursion(TreeNode<T>* root)
{
std::vector<T> v;
std::stack<TreeNode<T>*> st;
TreeNode<T>* cur = root; //当前节点
TreeNode<T>* prev = nullptr; //前一个访问的节点
while (cur || !st.empty())
{
//遍历左侧路径
while (cur)
{
st.push(cur);
cur = cur->_left;
}
TreeNode<T>* top = st.top();
//如果栈顶节点的右子节点为空,或刚刚遍历的节点prev是右子节点,那么访问,否则不放问,去走右子树
if (top->_right == nullptr || top->_right == prev)
{
//访问节点
v.push_back(top->_val);
st.pop();
prev = top;
}
else
{
cur = top->_right;
}
}
return v;
}