前言:
今天我们正式开始讲述算法中的排序。排序算法是我们十分重要的算法,为什么呢?
排序是在各种情况下都非常重要的,无论是在人类社会还是在计算机科学中。以下是一些排序的重要性:
-
数据分析:在数据分析中,对数据进行排序可以帮助我们更好地理解数据。例如,对销售数据按照时间顺序进行排序可以帮助我们了解产品销售的趋势。
-
搜索算法:在搜索算法中,排序可以帮助我们快速地找到需要的信息。例如,在搜索引擎中,对搜索结果按照相关性进行排序可以使用户更容易找到他们需要的信息。
-
数据库查询:在数据库查询中,对查询结果进行排序可以让我们更容易地查找特定的数据。例如,在一个包含大量客户信息的数据库中,对客户按照字母顺序进行排序可以让我们更轻松地查找特定客户的信息。
-
算法实现:在算法实现中,排序是一项基本的操作。例如,在许多排序算法中,我们需要对数据进行排序才能正确实现算法。
-
社交网络:在社交网络中,排序可以帮助我们更好地了解我们的朋友和关注者。例如,在Twitter中,对推文按照时间顺序进行排序可以让我们看到最新的内容。
总之,排序是在许多领域中都非常重要的操作,它可以帮助我们更好地理解和利用数据,提高我们的工作效率,以及实现各种算法和应用程序。
了解完排序算法的重要性,我们就来看看排序算法有哪些
- 冒泡排序(Bubble Sort)
- 选择排序(Selection Sort)
- 插入排序(Insertion Sort)
- 希尔排序(Shell Sort)
- 归并排序(Merge Sort)
- 快速排序(Quick Sort)
- 堆排序(Heap Sort)
- 计数排序(Counting Sort)
- 桶排序(Bucket Sort)
- 基数排序(Radix Sort)
- 拓扑排序(Topological Sort)
- 鸽巢排序(Pigeonhole Sort)
- 混合排序(Hybrid Sort)
- 推排序(Push Sort)
- 二叉树排序(Binary Tree Sort)
- 荷兰国旗排序(Dutch National Flag Sort)
- 优先队列排序(Priority Queue Sort)
- 外部排序(External Sort)
- 并行排序(Parallel Sort)
- 海量数据排序(Sort Big Data)
了解完排序算法的种类,我们就正式开始介绍今天要讲述的排序算法叭~
冒泡排序(Bubble Sort)
冒泡排序,就是它排序的过程就像冒泡泡一样,气泡从深处冒出水面,气泡会越来越大。
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就交换位置,直到没有任何一对数字需要比较为止。
其实它的实现过程也十分简单
- 比较相邻的两个元素,如果前一个元素比后一个元素大,则交换这两个元素的位置;
- 对每一对相邻的元素做同样的工作,从开始第一对到结尾的最后一对,这样一次遍历后,序列中最后一个元素一定是序列中的最大元素;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤 1~3,直到排序完成。
给大家看一下它的动图:
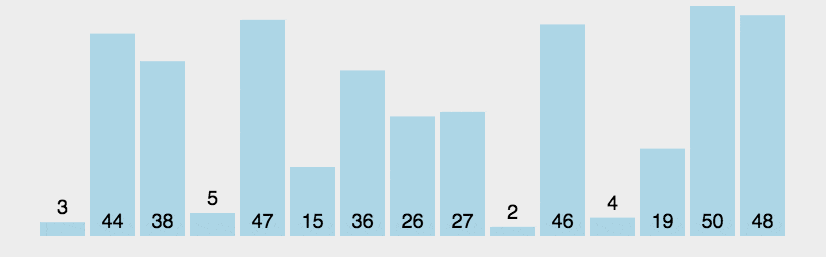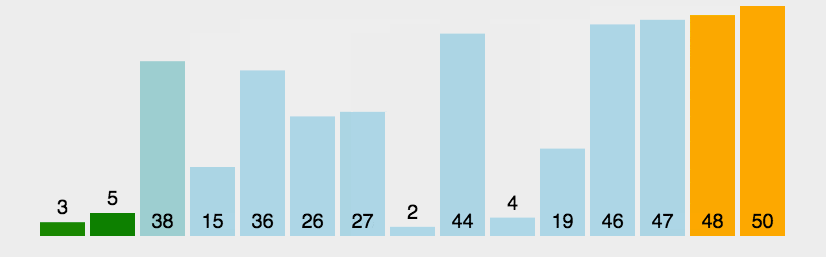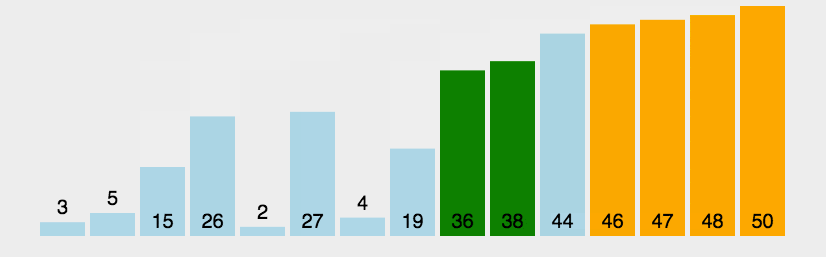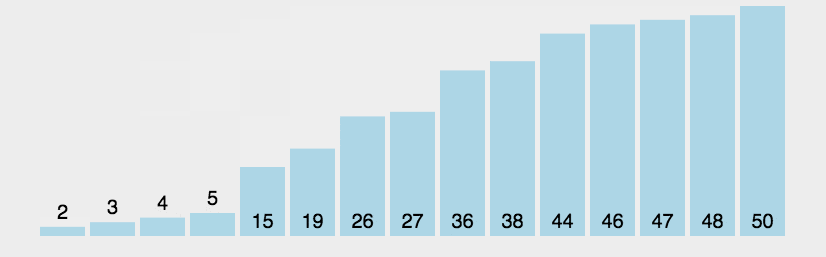
看完动图,会不会觉得形象了不少呢?
那么根据上述的实现过程,就开始写代码叭
//交换函数
void Swap(int* x1, int* x2)
{
int tmp = *x1;
*x1 = *x2;
*x2 = tmp;
}
//冒泡排序的实现
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
for (int j = 1; j < n - i; j++)
{
if (a[j - 1] > a[j])
{
Swap(&(a[j - 1]), &(a[j]));
}
}
}
}选择排序(Selection Sort)
选择排序,顾名思义,选择一个符合要求的数据放到指定的位置。它的基本思想是每次从未排序的数列中选出最小(或最大)的一个数,将其放在数列的起始位置,直到所有的数被排序完成为止。
它的实现过程也是十分的简单
- 从数列中找到最小(或最大)的数,将其放在数列的起始位置。
- 从剩余的未排序数列中找到最小(或最大)的数,将其放在已排序数列的末尾。
- 重复步骤2,直到所有的数被排序完成。
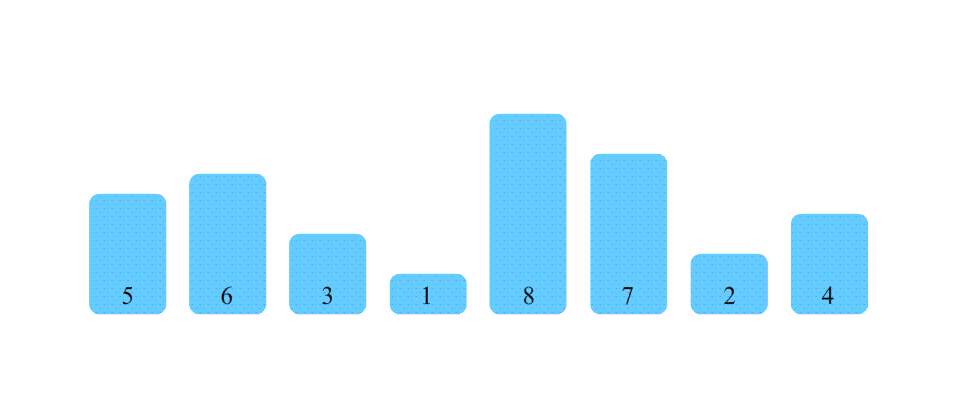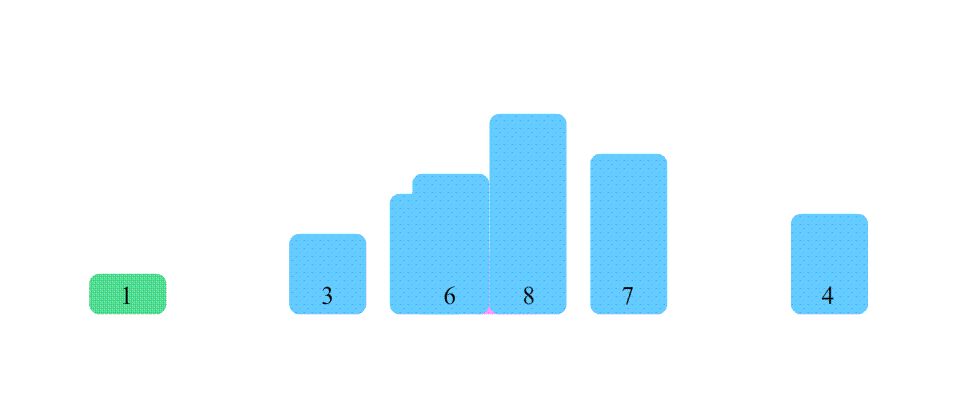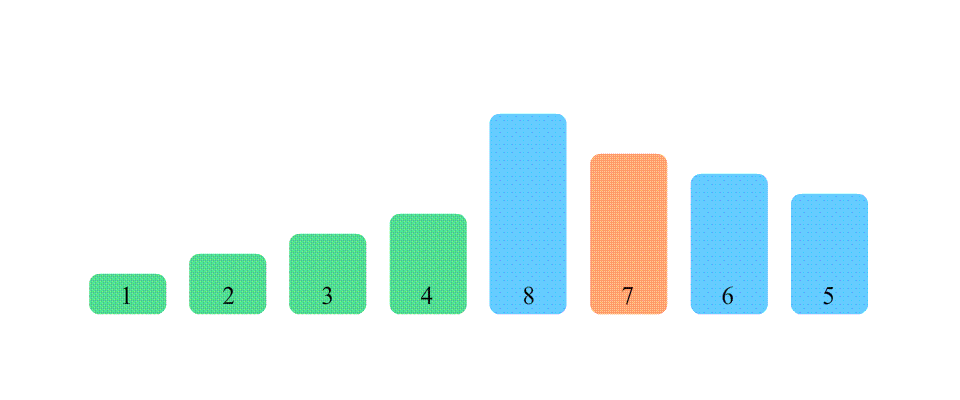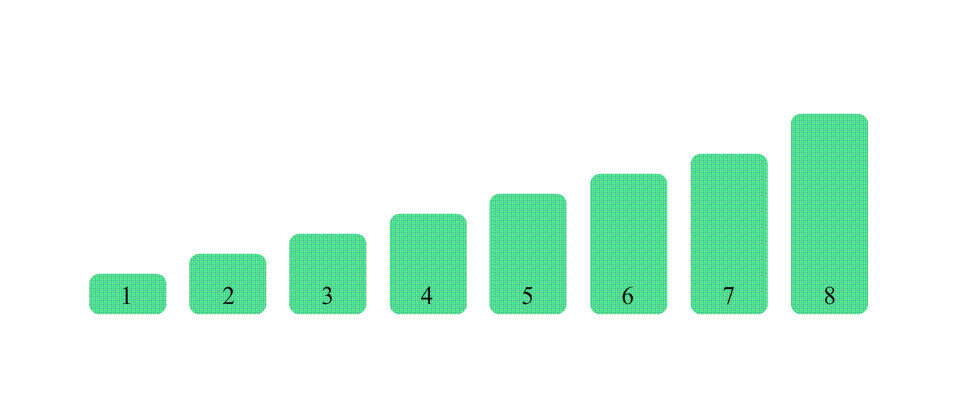
看完动图,马上就来完成代码
void SelectSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
int max = a[i];
for (int j = i+1; j < n; j++)
{
if (a[j] > max)
{
max = a[j];
}
}
}
}选择排序的核心思想是在未排序的数列中找到最小(或最大)的数,这个过程可以通过遍历数列来实现。具体来说,我们可以使用两个指针,一个指向已排序数列的末尾,一个指向未排序数列的起始位置,每次遍历未排序数列,找到最小(或最大)的数,将其与已排序数列的末尾交换位置。
插入排序(Insertion Sort)
说到插入排序,一定能想到斗地主的时候,拿着牌之后插到指定的位置,这个就是插入排序。将未排序的数列插入到已排序的数列中,使得插入后的数列仍然有序。
具体实现如下:
- 将数列分为已排序和未排序两部分,初始时已排序部分只包含第一个元素,未排序部分包含除第一个元素以外的所有元素。
- 从未排序部分中取出一个元素,将其插入到已排序部分中的适当位置,使得插入后的数列仍然有序。
- 重复步骤2,直到所有的数被排序完成。
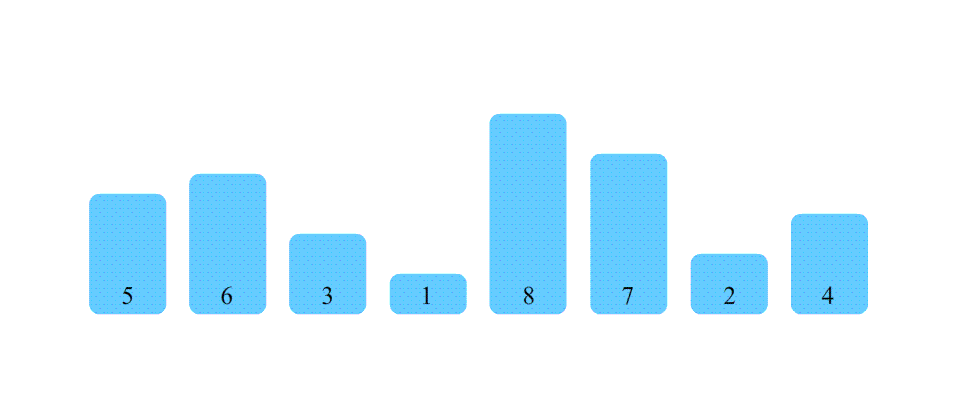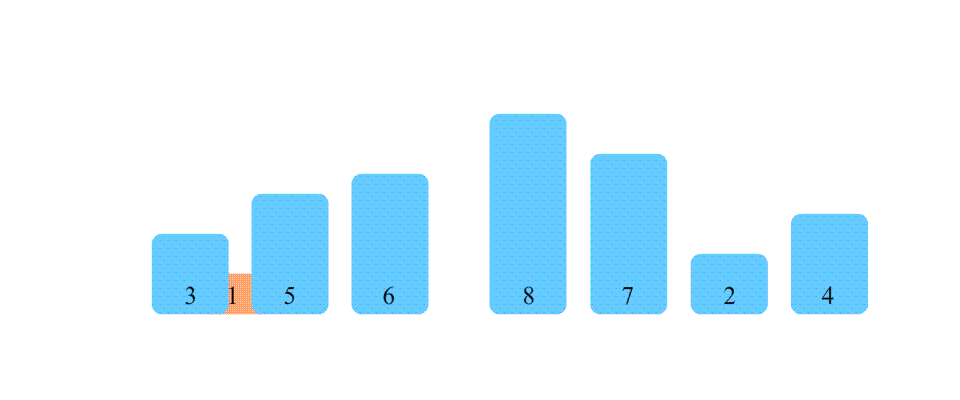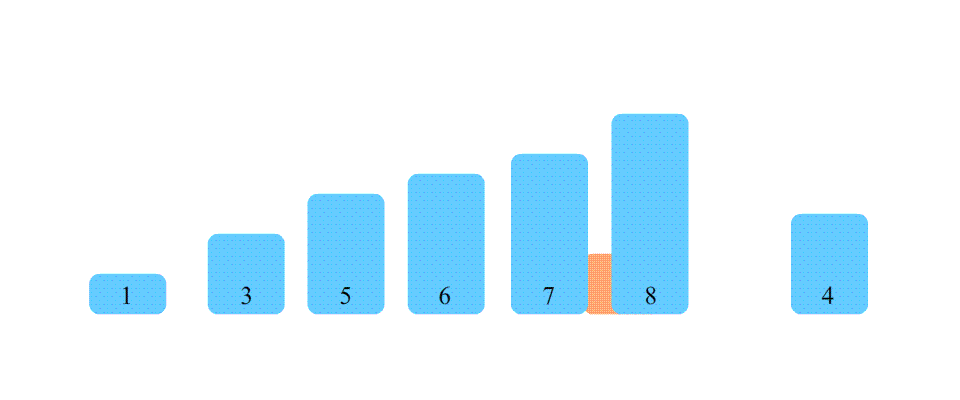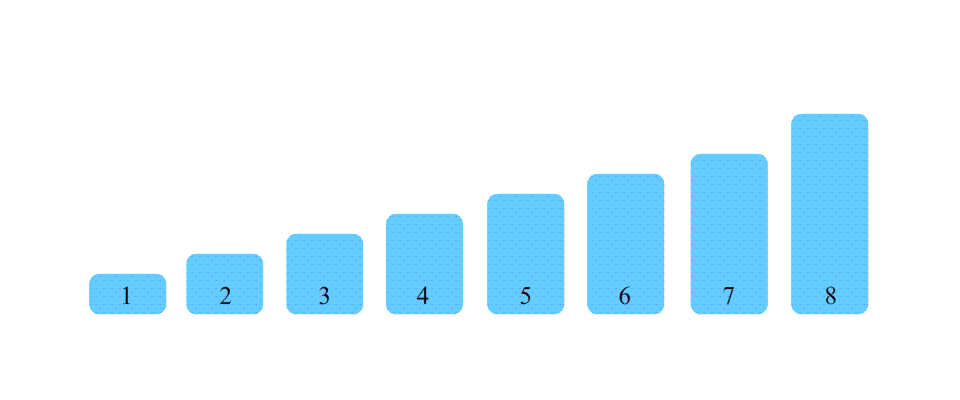
代码实现:
void InsertSort(int* a, int n)
{
for (int i = 1; i < n; i++)
{
int tmp = a[i];
for (int end = i - 1;end >=0 ; end--)
{
if (a[end] <= tmp)
{
a[end + 1] = tmp;
break;
}
if (a[end] > tmp)
{
a[end + 1] = a[end];
if (end == 0)
{
a[end] = tmp;
}
continue;
}
}
}
}插入排序的核心思想是将未排序的数列插入到已排序的数列中,这个过程可以通过遍历数列来实现。具体来说,我们可以使用一个指针指向未排序部分的第一个元素,然后将其插入到已排序部分中的适当位置。为了找到插入位置,我们可以从已排序部分的末尾开始遍历,依次比较已排序部分的元素和未排序部分的元素,直到找到一个比未排序元素小的元素,将未排序元素插入到这个元素的后面。
希尔排序(Shell Sort)
这个排序与上面的插入排序十分相似,甚至可以说一模一样,只不过这个排序能快速的把大的数放到后面去,而不是插入排序慢慢的一个一个的插入。它的创新之处在于引入了增量序列的概念,通过将数列划分为若干个子序列,对每个子序列进行插入排序,使得整个数列逐步变得有序,从而提高了排序的效率。
希尔排序的核心思想是将数列划分为若干个子序列,对每个子序列进行插入排序,使得整个数列逐步变得有序。
具体实现如下:
- 选择一个增量序列,将数列划分为若干个子序列,每个子序列包含相邻的若干个元素,其中相邻元素之间的距离为增量序列中的一个数。
- 对每个子序列进行插入排序,使得整个数列逐步变得有序。
- 重复步骤1和步骤2,直到增量序列中的最后一个数为1,即对整个数列进行插入排序。
还是先来看动图
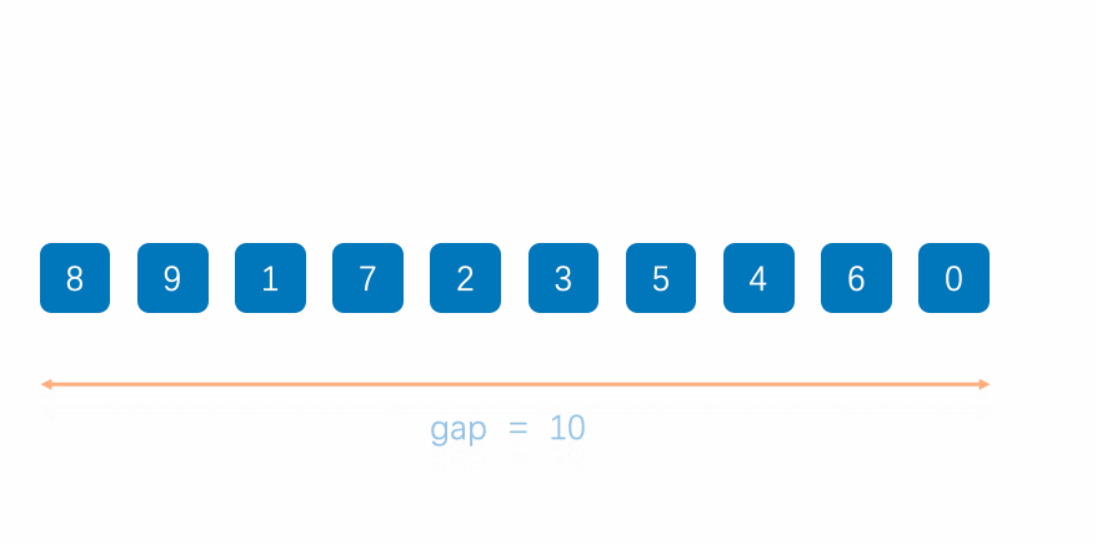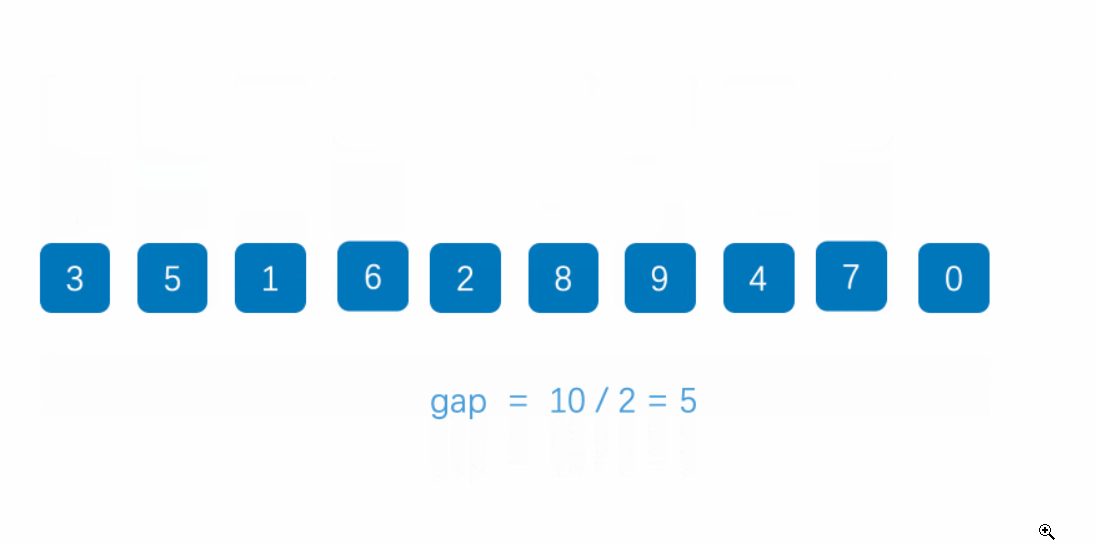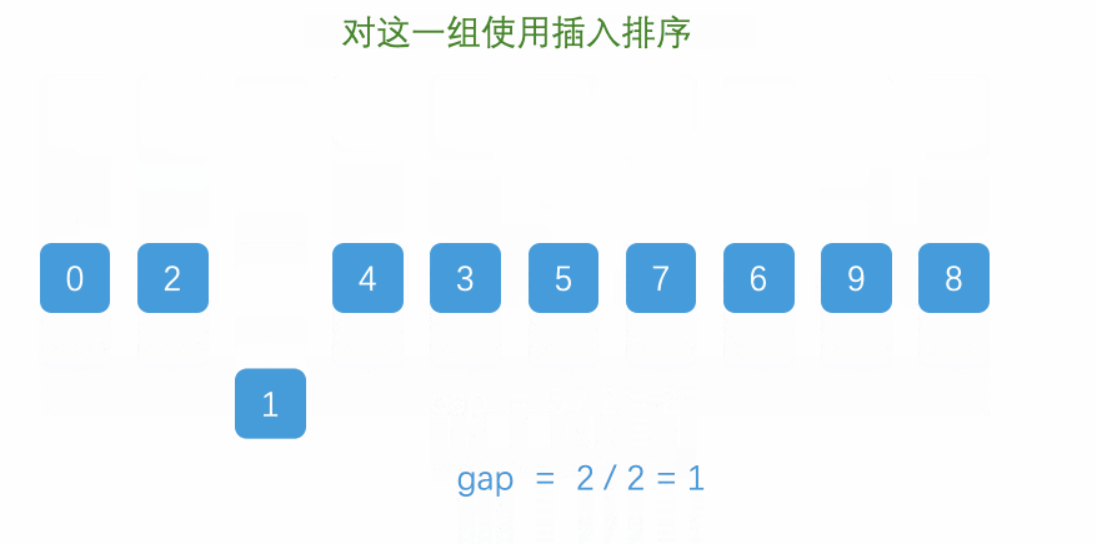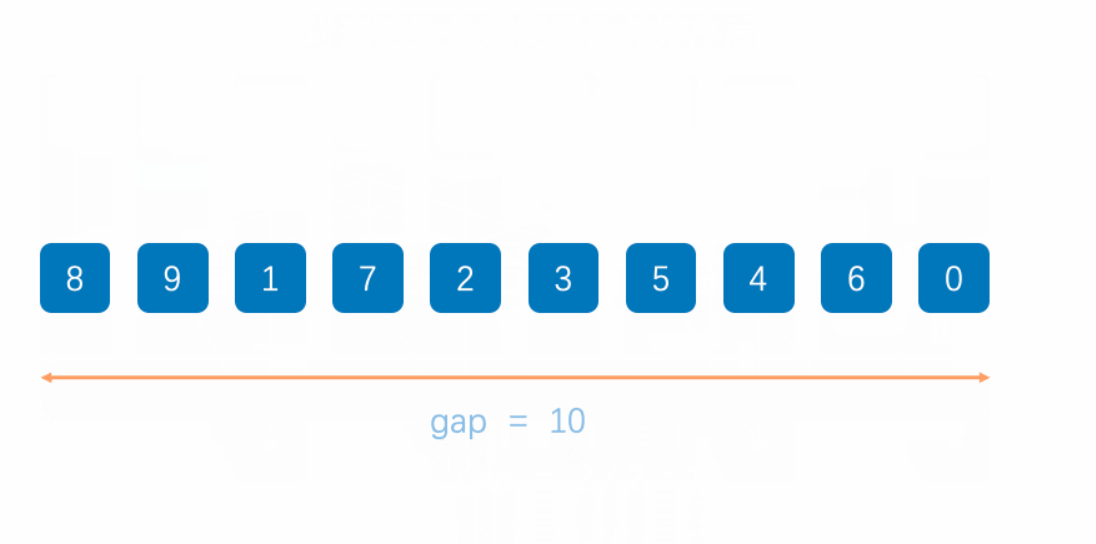
代码实现:
void ShellSort(int* arr, int n)
{
int gap;
int i = 0;
int j = 0;
int temp = 0;
for (int gap = n / 2; gap > 0; gap /= 2)
{
{
for (i = gap; i < n; i++)
{
temp = arr[i];
for (j = i; j >= gap && arr[j - gap] > temp; j -= gap)
{
arr[j] = arr[j - gap];
}
arr[j] = temp;
}
}
}
}