1时间复杂度计算
时间复杂度是什么?
一个函数,用大O表示,例如:O(1), O(N), O(logN).
定性描述算法的运行时间。
时间复杂度常见图:
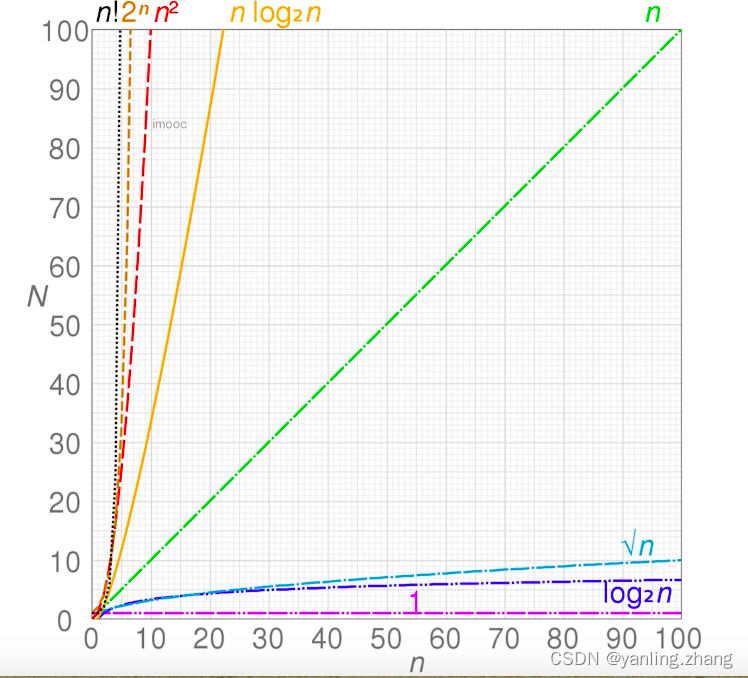
案例:
O(1)
let i = 0
i += 1
解释:每次执行这段代码,这段代码永远只会被执行一次,里面没有循环
O(n):
解释:在每次循环的时候都打印一次i,中间的for循环里面的代码被执行了n次,随着i的增大的增大,n也会增大
for (let i = 0; i < n; i+=1) {
console.log(i)
}
计算下面这段代码的时间复杂度:
相加:
如果两个时间复杂度,先后排列,我们就把各自的时间复杂度相加,而且,我们要取增长时间更快的时间复杂度,
O(1) + O(n) ,整体的时间复杂度是:O(n),因为,n足够大的时候,这个1可以忽略不计了。
let i = 0
i += 1
for (let i = 0; i < n; i+=1) {
console.log(i)
}
相乘
案例:
O(n) * O(n) = O(n ^ 2)
在for循环里面嵌套了另一个for循环,这个时候时间复杂度就是相乘。
for (let i = 0; i < n; i++) {
for (let j = 0; j < n; j++) {
console.log(i, j)
}
}
案例:
O(logN):
let i = 1;
while(i < n) {
console.log(i)
i *= 2
}
2.空间复杂度计算
空间复杂度计算是什么?
一个函数,用大O表示,例如:O(1), O(N), O(n ^ 2).
算法在运行过程中临时占用存储空间大小的度量。代码占用的存储空间,占用的存储空间越小越好。
案例:
O(1)
单个变量占用的内存看空间永远是1。永远是恒定的。
let i = 0;
i += 1
案例:
O(N):因为声明了一个list数组,在循环的时候向数组中添加值,它们相当于占用了n和内存,所以它的空间复杂度是O(N)
const list = []
for (let i = 0; i < n; i++) {
list.push(i)
}
案例:
O(n ^ 2):其实就是一个矩阵,矩阵说白了其实就是前端经常提的行,列,栅格布局。一行里面有几列。矩阵的本质就是一个二维数据,它存储了n的2次方的变量,所以这段代码的空间复杂度是:O(n ^ 2)
const matrix = []
for (let i = 0; i < n; i++) {
matrix.push([])
for (let j = 0; j < n; j++) {
matrix[i].push(j)
}
}