主成分分析
主成分分析是一种数据降维方式,他将大量相关变量转化为一组很少的不相关的变量,这些不相关的变量称为主成分。
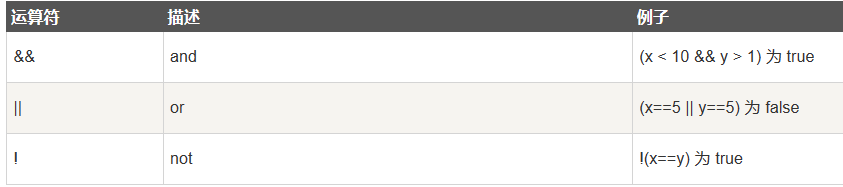
人话版:给你发一个由18位数字组成的身份证号码,第1、2位数字表示所在省份的代码;第3、4位数字表示所在城市的代码;第5、6位数字表示所在区县的代码;第7-14位数字表示出生年、月、日;第15-17位数字为顺序码,表示同一区域内同年同月同日出生的顺序号,其中第17位数字表示性别,奇数表示男性,偶数表示女性;第18位数字是校检码,校检码可以是0-9的数字,有时也用x表示,X是罗马数字的10。
这一串数字最后就可以表示你是哪个省的哪个市哪个县,出生日期和性别。
本来关于你的很多信息(变量)抽象成了一串数字(主成分PC),就可以表示你的很多信息了。<==我觉得像是在打包,具体的降维过程和算法参见博客。
brief

实例
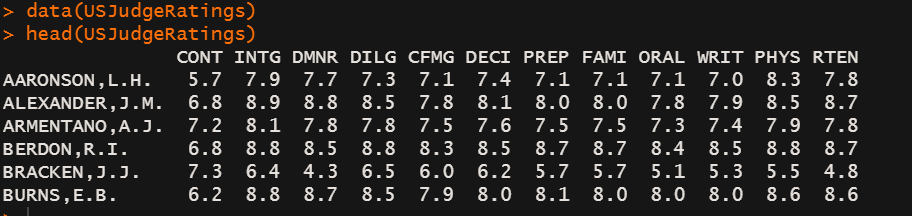
在这个数据集USJudgeRatings中,每一行为一个律师,每一列对应着这个律师某一方面的一些评价打分,可以用较少的变量代替上述的列变量吗?大约多少个合适?如何计算呢?
判断需要多少个主成分数目
- 直接指定
- 根据方差累积的阈值判断,也就是多少个PC之后对数据的方差解释贡献度较小 ⇐ 这个方法最常用
- 根据相关性矩阵判断大概可以聚成几个类
下面使用手肘法和平行分析判断选取多少个PC
- 手肘法–碎石图
可以简单理解为Y轴是PC个数,X轴是累积方差解释度,陡峭拐点之前的哪些PC对数据的方差解释度最好,可以选取这些PC进行后续分析。 - 平行分析
模拟一个相同大小的K*K的随机数矩阵,计算他们的平均特征值,若真实数据的特征值大于模拟数据的平均特征值,对应的PC则可以保留下来。
library(psych)
fa.parallel(USJudgeRatings[,-1], fa="pc", n.iter=100,
+ show.legend=FALSE, main="Scree plot with parallel analysis")
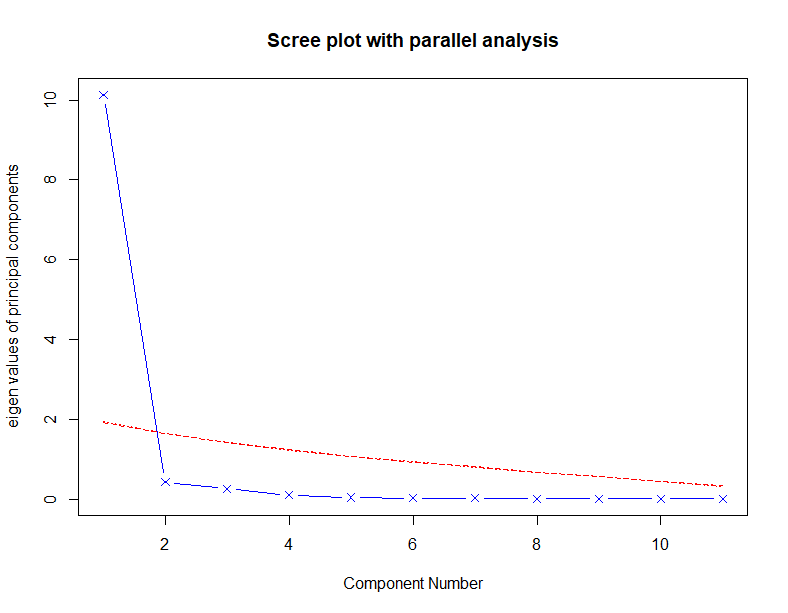
蓝色线是碎石图,component number等于2的时候是拐点,所以PC=1或者2都可以
红色线是平行分析模拟出来的平均特征值分布曲线,只有component number等于1时,真实数据的特征值才大于模拟数据的特征值,综合来看可以让PC=1.
提取主成分
principal函数可以根据原始矩阵或者相关性系数矩阵做主成分分析,需要注意NA值以及太多的zero值的影响。

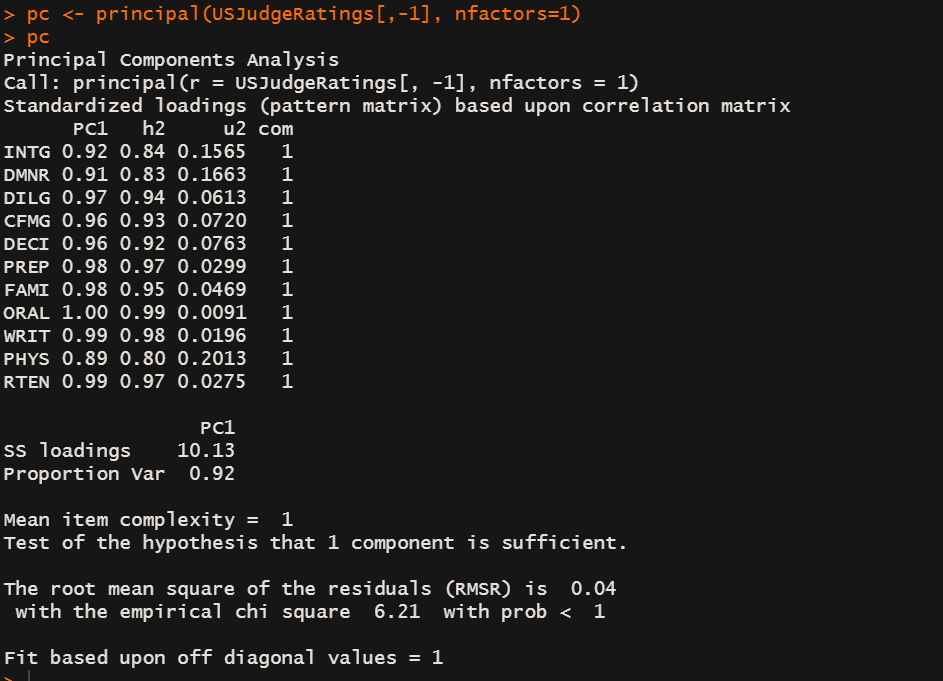
- 上述的截图中包含了成分载荷,指观测的变量与主成分的相关系数,
形如 PC1 = 0.92 * INTG + 0.91 * DMNR… ,该等式用于计算PC得分,其中0.92,0.91,0.97称为载荷。 - 上面那个matrix PC1列是成分载荷,h2列表示成分公因子方差,即主成分对每个变量的方差解释度。u2表示成分唯一性,即方差无法被主成分解释的部分(1-h2)。
- 上述变量中体能(PHYS) 80 %的方差都可以被第一主成分解释,相比而言也是第一主成分表示性最差的变量
- SS loadings 行包含了与主成分相关连的特征值,指的是与特定主成分相关连的标准化后的方差值。
- Proportion Var 表示的是每个主成分对整个数据集的解释度。
主成分旋转
旋转是让成分载荷矩阵变得更容易解释的数学方法,它们尽可能地对成分降噪。
目前有两种旋转方法,一是让成分保持不相关(正交旋转),二是让他们变得相关(斜交相关)。
最流行的是正交旋转中的方差最大旋转法,即让每一列的载荷只有很大的几个载荷,其他都是很小的载荷
因为需要正交旋转,上述的数据集只有一个PC不好演示,我们换一个数据集。
Harman23.cor 数据集中的cov数据槽是一个305名女孩的身体指标的相关性系数矩阵。
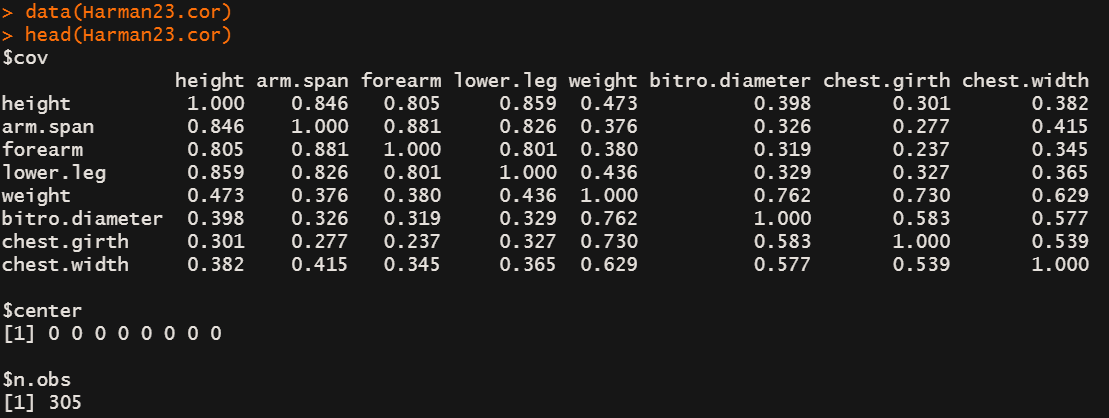
fa.parallel(Harman23.cor$cov, n.obs=302, fa="pc", n.iter=100,
show.legend=FALSE, main="Scree plot with parallel analysis")
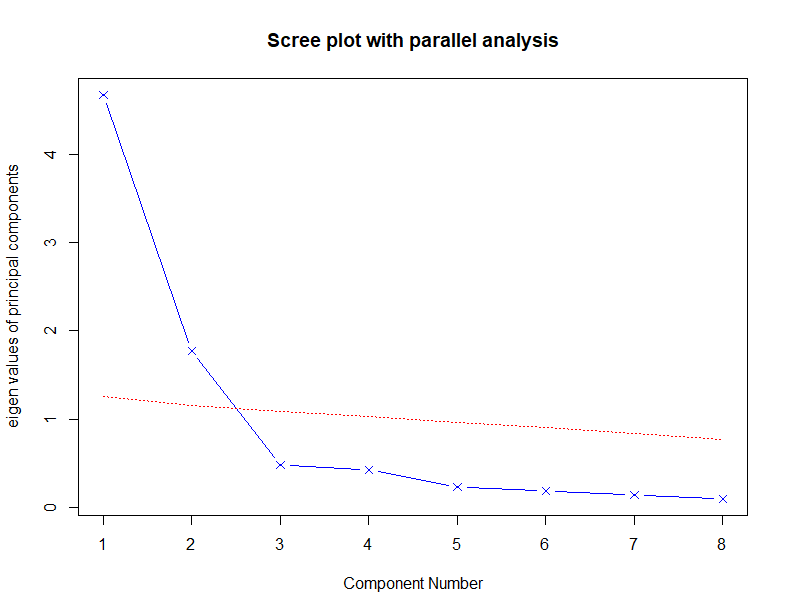
-
不进行旋转
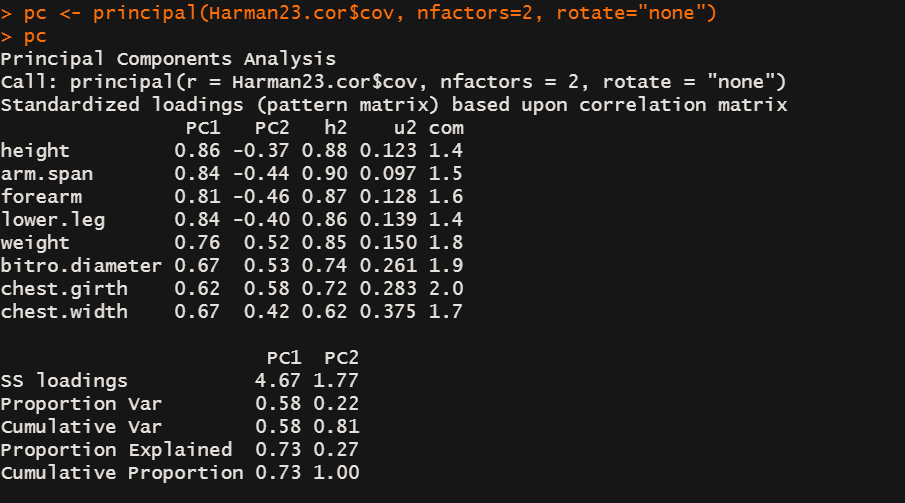
PC1 = 0.86 * height + 0.84 * arm.span …
PC2 = -0.37 * height -0.44 * arm.span … + 0.58 * chest.girth + 0.42 * chest.width
PC1 与 PC2 可以解释身高 heigh 88%的方差
proportion var 列表示 PC1 可以解释数据集 58%的方差,PC2 可以解释数据集 22%的方差,累加一起81% -
进行旋转
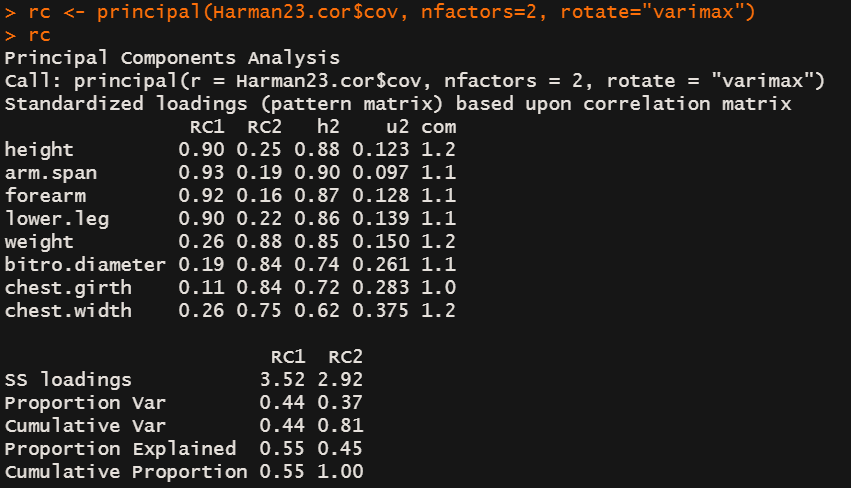
- PC 变成了RC 表示以旋转
- 累计方差解释度没变,但是每个成分对数据集的方差解释度发生细微改变
- 前四个变量在RC1中相关性/贡献度比较大,在RC2中贡献度较小,和未旋转的结果很类似,尤其你看h2那一列数据,旋转和未旋转是一样的。那旋转的好处是什么呢?降噪 – 变量的贡献度分化了,大的变大,小的变小,一眼看出来差别了。
获取主成分得分
输入是原始数据

输入是相关性矩阵