认识动态规划
动态规划的求解思路:
1. 把一个问题分解成若干个子问题
2. 将中间结果保存以避免重复计算
基本步骤:
1. 找出最优解的性质,然后刻画结构特征 (找规律)
2. 最优解(最好的解决方案 定义) 循环(递归)
3. 以自上而下或者自下而上的方式来计算最优值(局部的)
4. 通过最优值来构造最优解
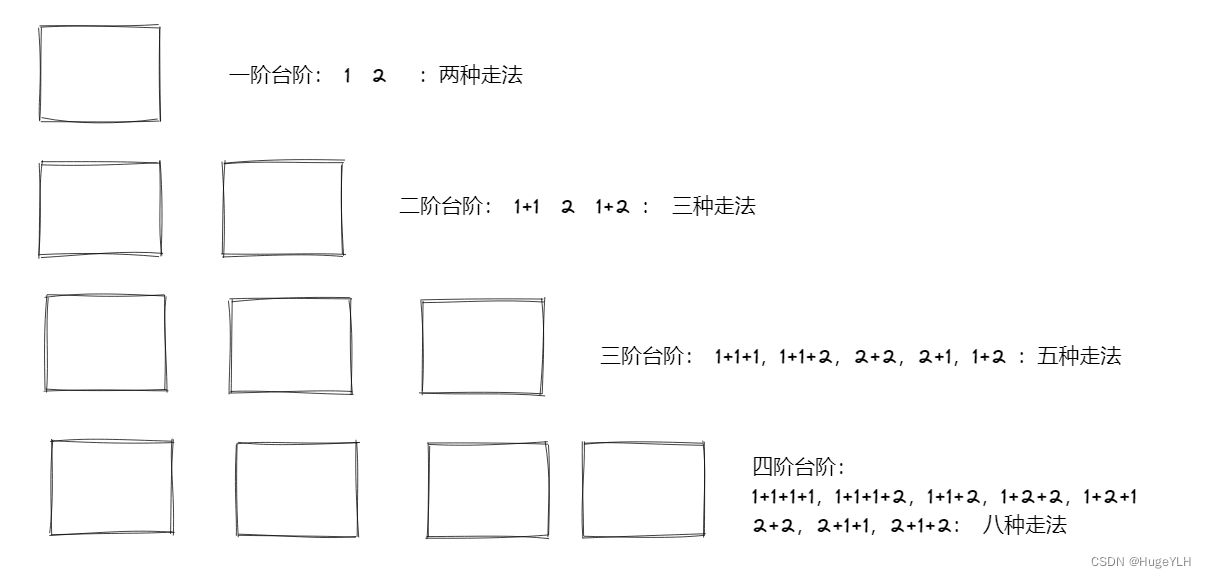
走台阶问题
你每次可以走一步或者两步,有n个台阶,请问你可以有多少种不同的走的方案。
规定:可以超过n,例如n=4: 你可以选择这样走: 1+2+2 ,即使最后答案是5
解析:
走台阶问题就是最简单的动态规划的问题:
我们可以将每一次走的过程分解:
一阶台阶,我们总共有两种方案。
二阶台阶,我们有三种方案。…
你有没有发现很熟悉? 这不就是我们的斐波那契数列吗? 1 1 2 3 5 8 …
只不过这个斐波那契数列是从2开始的,然后依次往下走。
动态规划:
int func1(int n)
{
if (n == 1 || n == 2)
{
return n;
}
else
{
return func1(n - 1) + func1(n - 2);
}
}
最短路径问题
求最短路径问题: 有矩阵 map 能且只能两种走法 往下 或者 往右 求最短路径
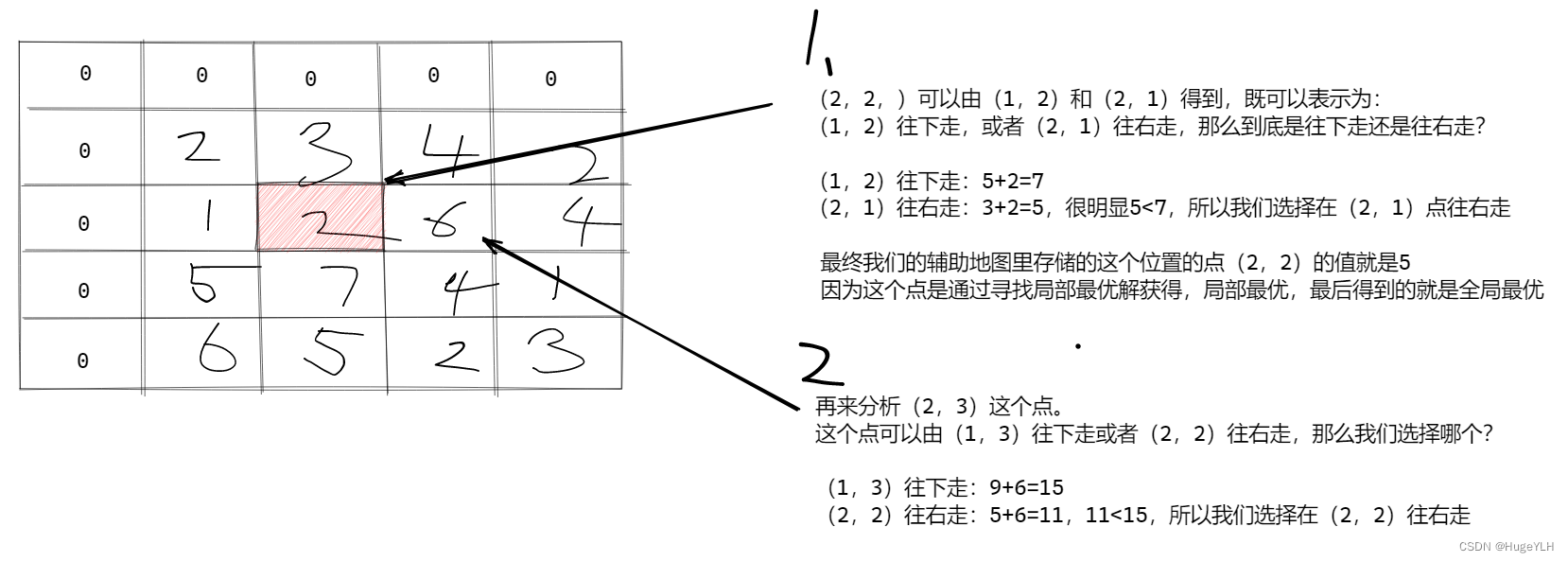
注意:我们构造的辅助数组的宽高要比原数组大一,原因:
- 在我们处理第一行与第一列的时候,第一行往右走;第一列往下走。
- i== 0 或者 j== 0的时候会出现数组越界,因此必须要单独空出第一行与第一列的空间,在剩下的空间处理原地图。
地图数组
int map[4][4]{
2,3,4,2,
1,2,6,4,
5,7,4,1,
6,5,2,3,
};
//动态规划2:最短路径
void func2()
{
//1. 准备一个辅助数组
int tempArr[5][5]{};
//2. 寻找每一步的最小值,当前最小值累计起来就是最后的最小值
//即由 局部最优解--->全局最优解
for (int i = 1; i < 5; i++)
{
for (int j = 1; j < 5; j++)
{
//第一行:只能从左边过来
if (i == 1)
{
tempArr[i][j] = map[i-1][j-1] + tempArr[i][j - 1];
}
//第一列:只能从上边下来
else if (j == 1)
{
tempArr[i][j] = map[i-1][j-1] + tempArr[i - 1][j];
}
else
{
//分别计算从左边《往右》和从上边《往下》的最小值,寻找局部最优解
tempArr[i][j] = map[i-1][j-1] + min(tempArr[i][j - 1], tempArr[i - 1][j]);
}
}
}
printf("地图的最短路径: %d\n", tempArr[4][4]);
}
辅助地图:

最长上升子串问题
有一串整数数组,1 4 7 2 5 8 3 6 9
求出其最长的上升字串的长度
上升串是这样的:
147 258 369
上升串允许是不连续的: 1 4 7 8 9
我们经过分析,求总的最长的字串,其实就是求每个点之前的最长长度
- 使用pMaxlen记录每一个点对应的最长的长度。
- 使用pTemp记录用来确定每个点的最长字串长度,每次遍历都从数组头部开始,遍历到对应点为止。
- pMaxLen数组记录这个点的最长字串长度,他的值是由pTemp来确定。
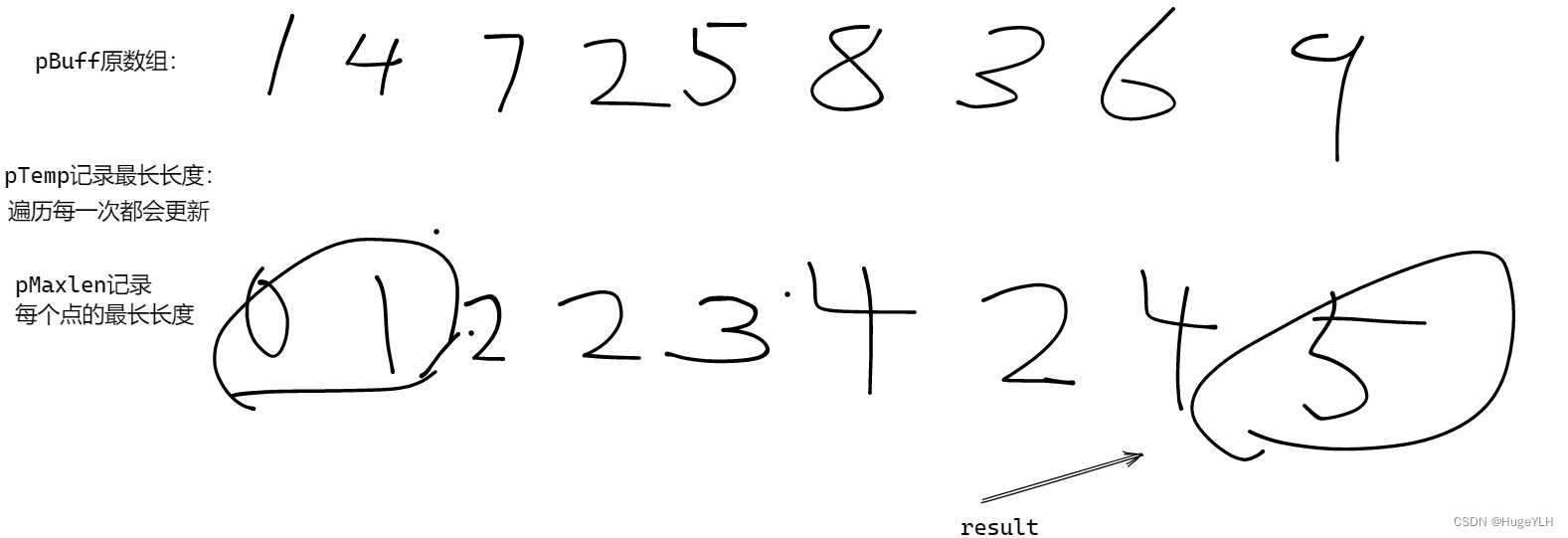
//动态规划3:最长上升字串
void func3()
{
//1. 预处理
int len = 0;
printf("请输入数组长度: ");
cin >> len;
int* pBuff = new int[len] {};
for (int i = 0; i < len; i++)
{
cin >> pBuff[i];
}
//2. pMaxLen数组
int* pMaxLen = new int[len] {};
//pMaxLen数组:第一个元素对应点的最长字串我们初始化为 0
//第二个元素对应点的最长字串我们初始化为 1,因为他前面就一个字符,我们默认1就是最长的
pMaxLen[1] = 1;
//从第三个字符开始遍历
for (int i = 2; i < len; i++)
{
int pTemp = 1; //从第三个字符开始,所以前面最长的一定是从1开始
for (int j = 1; j < i; j++) //在i的前面寻找
{
//前面小于后面,满足上升条件,更新pTemp记录长度
if (pBuff[j] < pBuff[i])
{
pTemp = max(pTemp, pMaxLen[j]);
}
pMaxLen[i] = pTemp + 1;
}
}
printf("最长上升字串: %d\n", pMaxLen[len - 1]);
delete[] pBuff;
}