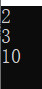---

一、多线程同步

竞争与协作

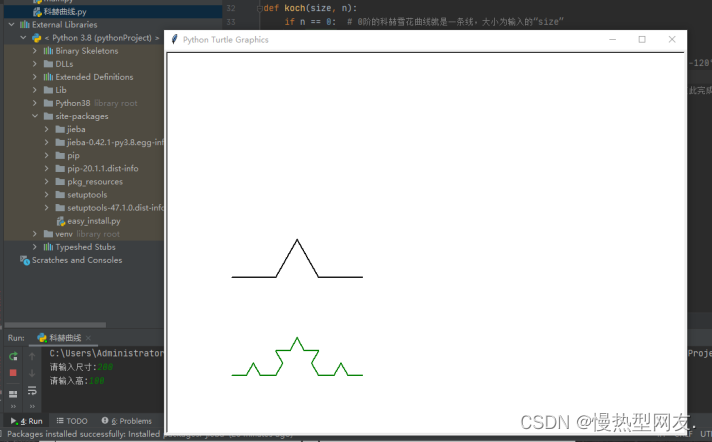
在单核 CPU 系统⾥，为了实现多个程序同时运⾏的假象，操作系统通常以时间⽚调度的⽅式， 让每个进程
执⾏每次执⾏⼀个时间⽚，时间⽚⽤完了，就切换下⼀个进程运⾏，由于这个时间⽚的时间很短，于是就造成了「并发」的现象。

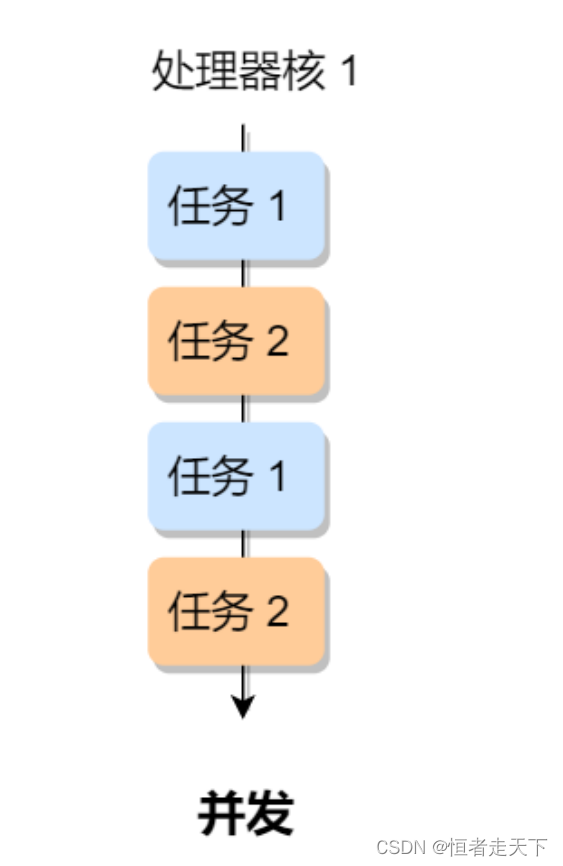
另外，操作系统也为每个进程创建巨⼤、私有的虚拟内存的假象，这种地址空间的抽象让每个程序好像拥
有⾃⼰的内存，⽽实际上操作系统在背后秘密地让多个地址空间「复⽤」物理内存或者磁盘。

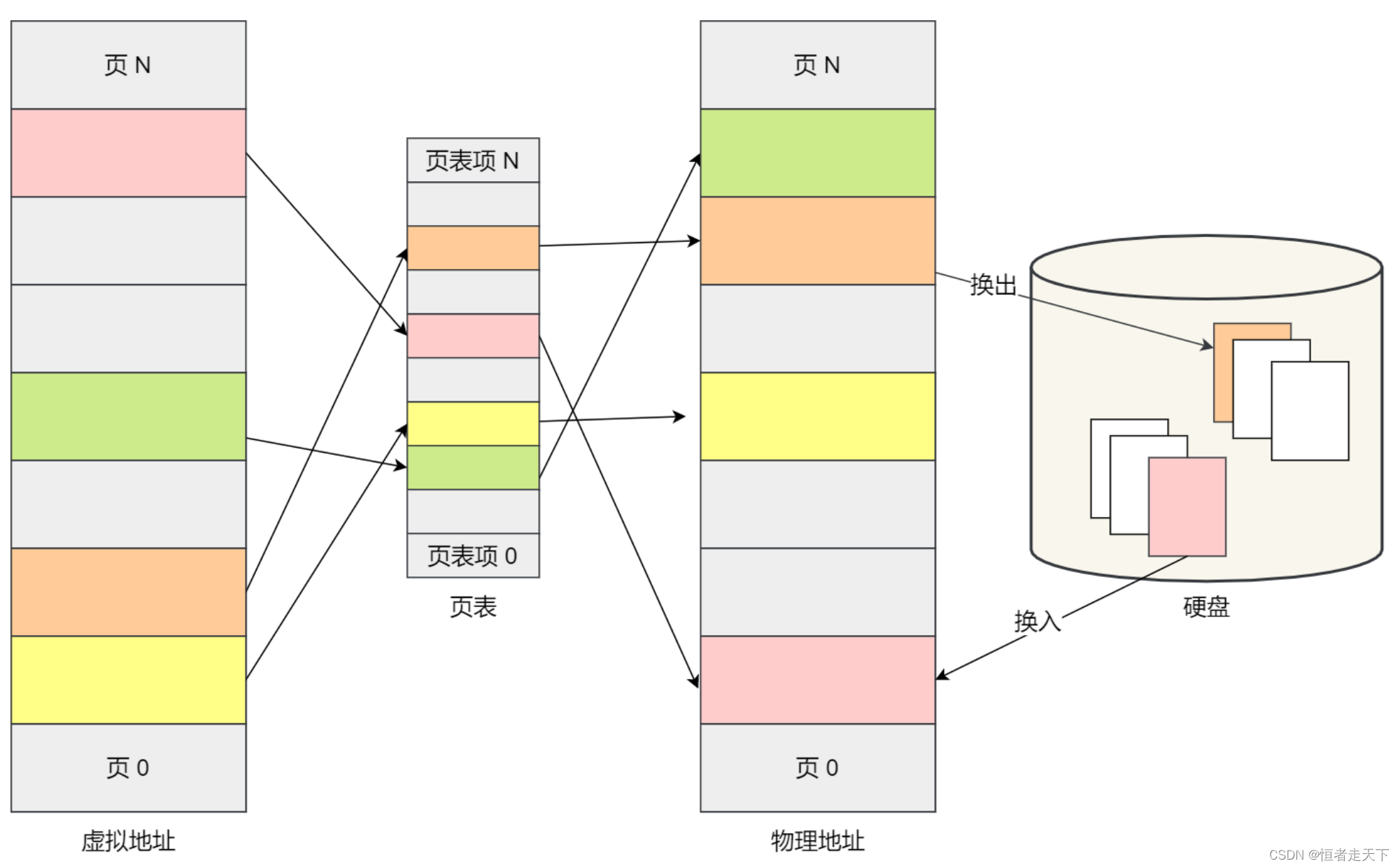
如果⼀个程序只有⼀个执⾏流程，也代表它是单线程的。当然⼀个程序可以有多个执⾏流程，也就是所谓
的多线程程序，线程是调度的基本单位，进程则是资源分配的基本单位。

所以，线程之间是可以共享进程的资源，⽐如代码段、堆空间、数据段、打开的⽂件等资源，但每个线程
都有⾃⼰独⽴的栈空间。

那么问题就来了，多个线程如果竞争共享资源，如果不采取有效的措施，则会造成共享数据的混乱。

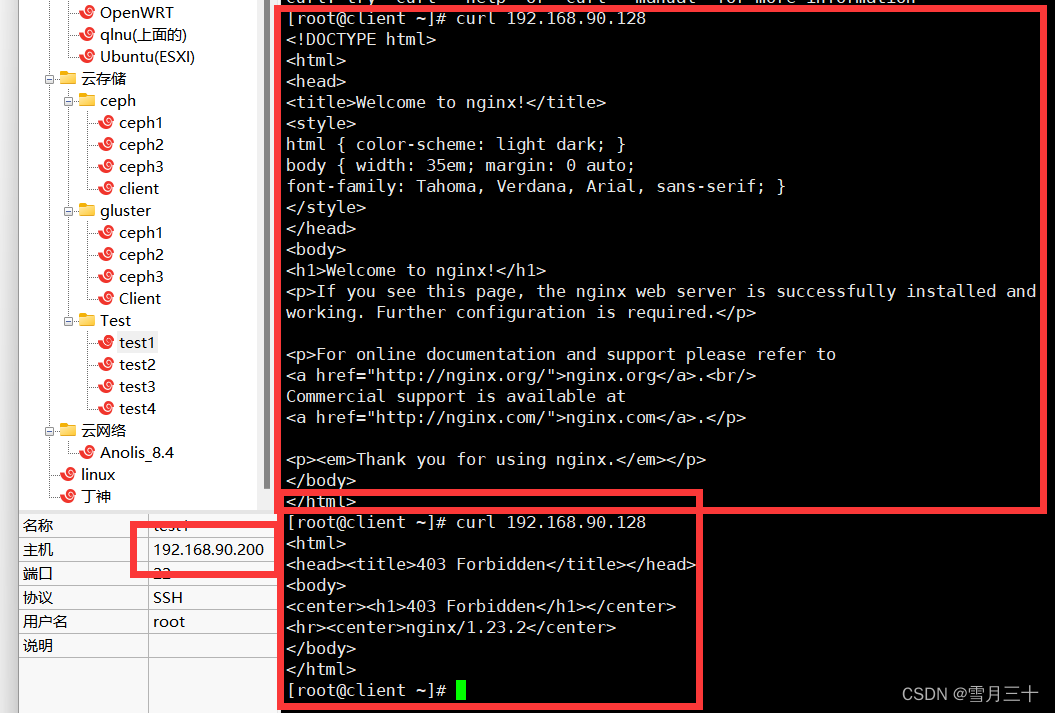
我们做个⼩实验，创建两个线程，它们分别对共享变量 i ⾃增 1 执⾏ 10000 次，如下代码（虽然说
是 C++ 代码，但是没学过 C++ 的同学也是看到懂的）：

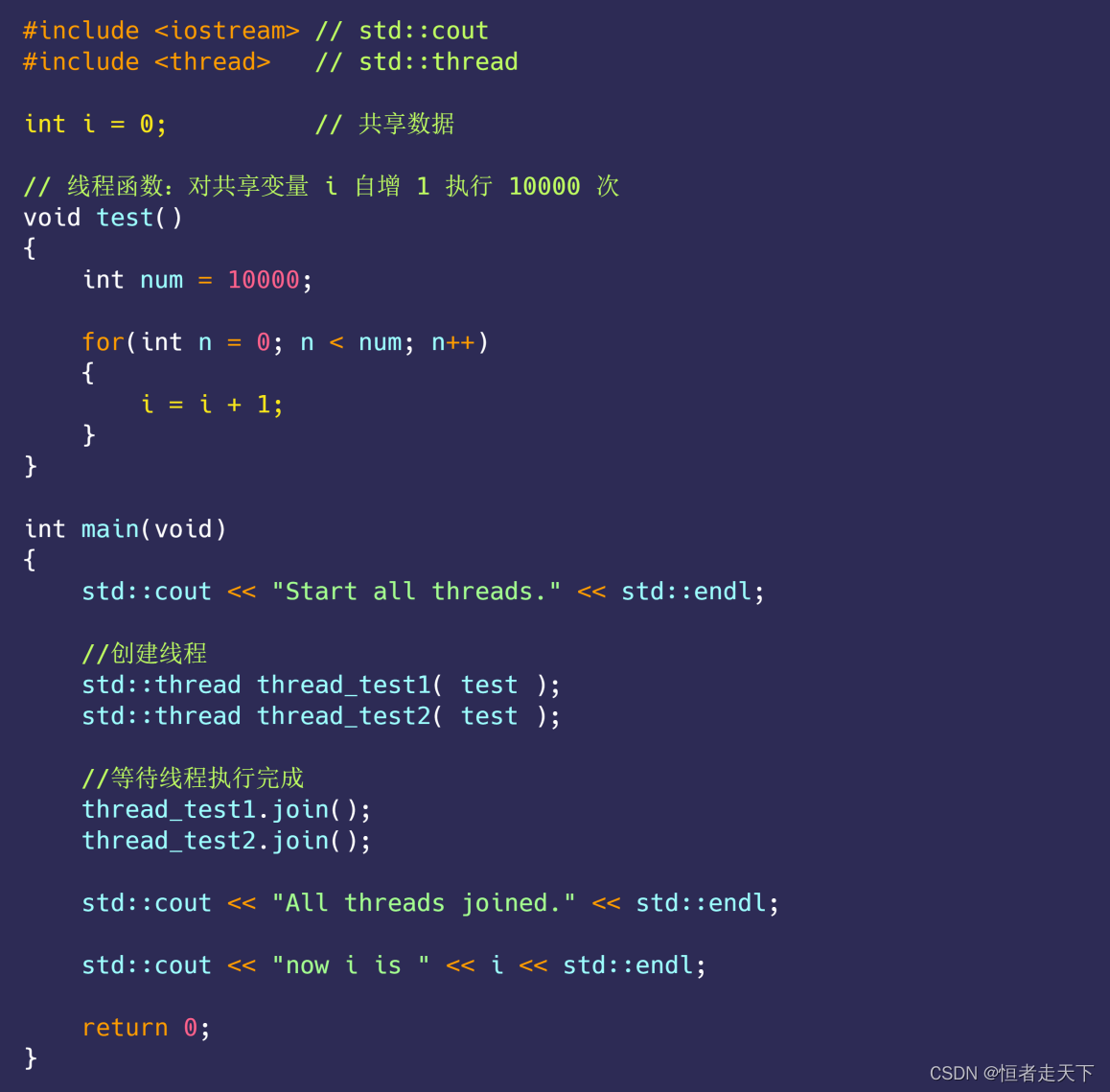
按理来说， i 变量最后的值应该是 20000 ，但很不幸，并不是如此。我们对上⾯的程序执⾏⼀下：

运⾏了两次，发现出现了 i 值的结果是 15173 ，也会出现 20000 的 i 值结果。
每次运⾏不但会产⽣错误，⽽且得到不同的结果。在计算机⾥是不能容忍的，虽然是⼩概率出现的错误，
但是⼩概率事件它⼀定是会发⽣的，「墨菲定律」⼤家都懂吧。

为什么会发⽣这种情况？
为了理解为什么会发⽣这种情况，我们必须了解编译器为更新计数器 i 变量⽣成的代码序列，也就是要了
解汇编指令的执⾏顺序。
在这个例⼦中，我们只是想给 i 加上数字 1，那么它对应的汇编指令执⾏过程是这样的：

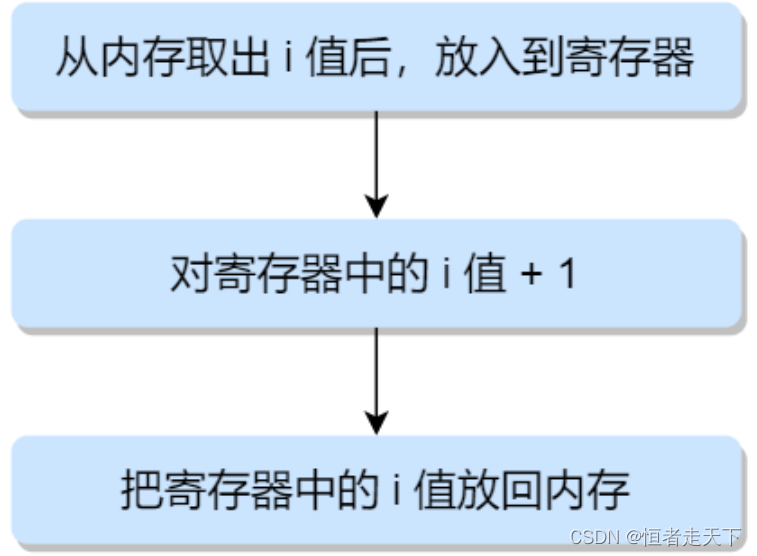
可以发现，只是单纯给 i 加上数字 1，在 CPU 运⾏的时候，实际上要执⾏ 3 条指令。

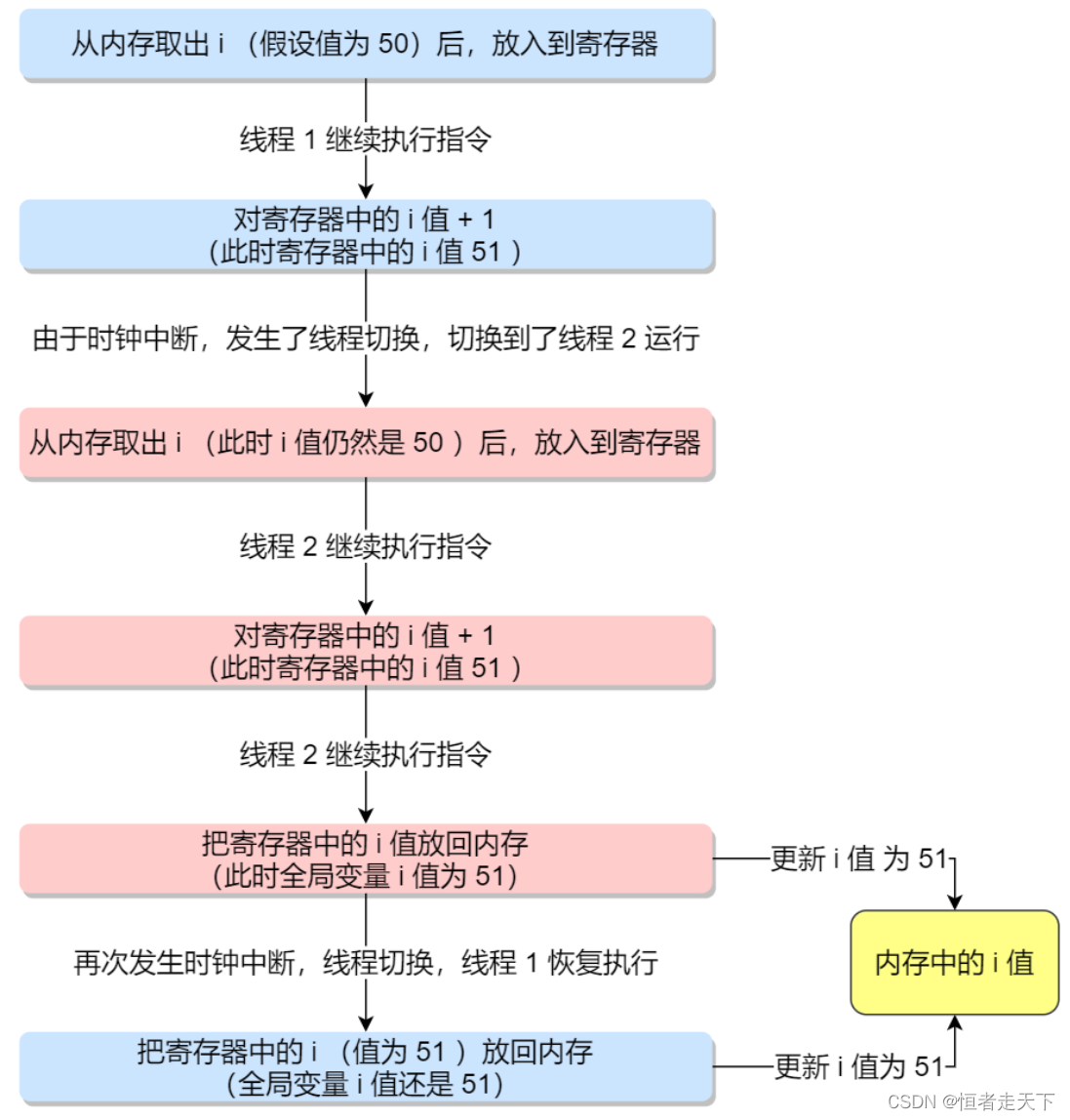
设想我们的线程 1 进⼊这个代码区域，它将 i 的值（假设此时是 50 ）从内存加载到它的寄存器中，然后它
向寄存器加 1，此时在寄存器中的 i 值是 51。

现在，⼀件不幸的事情发⽣了：时钟中断发⽣。因此，操作系统将当前正在运⾏的线程的状态保存到线程
的线程控制块 TCB。

现在更糟的事情发⽣了，线程 2 被调度运⾏，并进⼊同⼀段代码。它也执⾏了第⼀条指令，从内存获取 i
值并将其放⼊到寄存器中，此时内存中 i 的值仍为 50，因此线程 2 寄存器中的 i 值也是 50。假设线程 2 执
⾏接下来的两条指令，将寄存器中的 i 值 + 1，然后将寄存器中的 i 值保存到内存中，于是此时全局变量 i
值是 51。

最后，⼜发⽣⼀次上下⽂切换，线程 1 恢复执⾏。还记得它已经执⾏了两条汇编指令，现在准备执⾏最后
⼀条指令。回忆⼀下， 线程 1 寄存器中的 i 值是51，因此，执⾏最后⼀条指令后，将值保存到内存，全局
变量 i 的值再次被设置为 51。

简单来说，增加 i （值为 50 ）的代码被运⾏两次，按理来说，最后的 i 值应该是 52，但是由于不可控的调
度，导致最后 i 值却是 51。

针对上⾯线程 1 和线程 2 的执⾏过程，我画了⼀张流程图，会更明确⼀些：

互斥的概念

上⾯展示的情况称为竞争条件（race condition），当多线程相互竞争操作共享变量时，由于运⽓不好，
即在执⾏过程中发⽣了上下⽂切换，我们得到了错误的结果，事实上，每次运⾏都可能得到不同的结果，
因此输出的结果存在不确定性（indeterminate）。

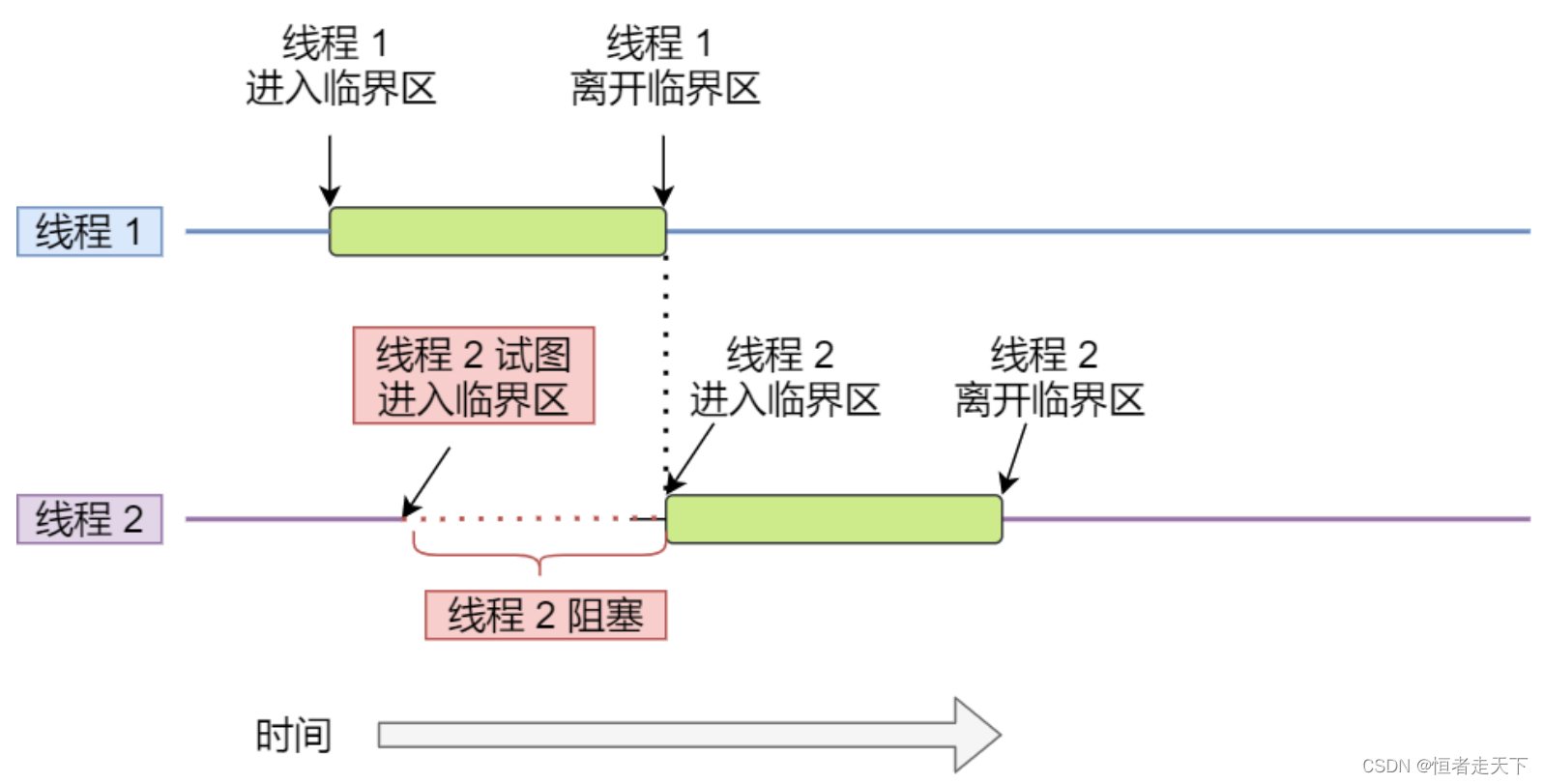
由于多线程执⾏操作共享变量的这段代码可能会导致竞争状态，因此我们将此段代码称为临界区（critical
section），它是访问共享资源的代码⽚段，⼀定不能给多线程同时执⾏。

我们希望这段代码是互斥（mutualexclusion）的，也就说保证⼀个线程在临界区执⾏时，其他线程应该
被阻⽌进⼊临界区，说⽩了，就是这段代码执⾏过程中，最多只能出现⼀个线程。

另外，说⼀下互斥也并不是只针对多线程。在多进程竞争共享资源的时候，也同样是可以使⽤互斥的⽅式
来避免资源竞争造成的资源混乱。

同步的概念

互斥解决了并发进程/线程对临界区的使⽤问题。 这种基于临界区控制的交互作⽤是⽐较简单的，只要⼀个
进程/线程进⼊了临界区，其他试图想进⼊临界区的进程/线程都会被阻塞着，直到第⼀个进程/线程离开了
临界区。

我们都知道在多线程⾥，每个线程并不⼀定是顺序执⾏的，它们基本是以各⾃独⽴的、不可预知的速度向
前推进，但有时候我们⼜希望多个线程能密切合作，以实现⼀个共同的任务。

例⼦，线程 1 是负责读⼊数据的，⽽线程 2 是负责处理数据的，这两个线程是相互合作、相互依赖的。线
程 2 在没有收到线程 1 的唤醒通知时，就会⼀直阻塞等待，当线程 1 读完数据需要把数据传给线程 2 时，
线程 1 会唤醒线程 2，并把数据交给线程 2 处理。

所谓同步，就是并发进程/线程在⼀些关键点上可能需要互相等待与互通消息，这种相互制约的等待与互通
信息称为进程/线程同步。

举个⽣活的同步例⼦，你肚⼦饿了想要吃饭，你叫妈妈早点做菜，妈妈听到后就开始做菜，但是在妈妈没
有做完饭之前，你必须阻塞等待，等妈妈做完饭后，⾃然会通知你，接着你吃饭的事情就可以进⾏了。

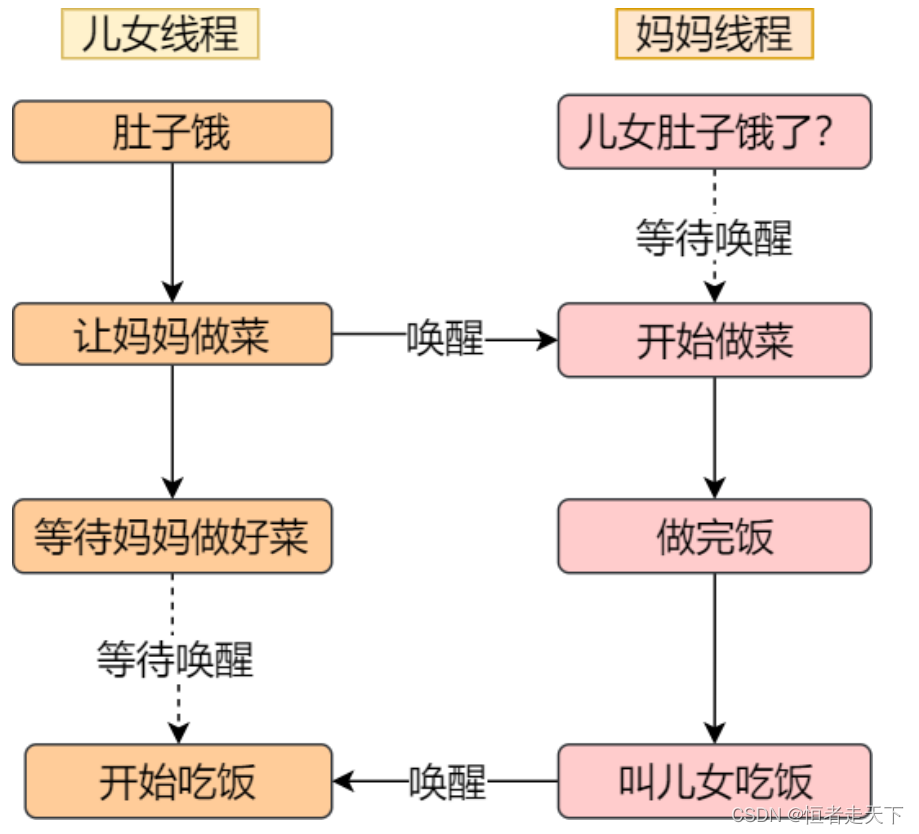
注意，同步与互斥是两种不同的概念：

• 同步就好⽐：「操作 A 应在操作 B 之前执⾏」，「操作 C 必须在操作 A 和操作 B 都完成之后才能执
  ⾏」等；
• 互斥就好⽐：「操作 A 和操作 B 不能在同⼀时刻执⾏」；

互斥与同步的实现和使⽤

在进程/线程并发执⾏的过程中，进程/线程之间存在协作的关系，例如有互斥、同步的关系。
为了实现进程/线程间正确的协作，操作系统必须提供实现进程协作的措施和⽅法，主要的⽅法有两种：

• 锁：加锁、解锁操作；
• 信号量：P、V 操作；

这两个都可以⽅便地实现进程/线程互斥，⽽信号量⽐锁的功能更强⼀些，它还可以⽅便地实现进程/线程同
步。

锁

使⽤加锁操作和解锁操作可以解决并发线程/进程的互斥问题。

任何想进⼊临界区的线程，必须先执⾏加锁操作。若加锁操作顺利通过，则线程可进⼊临界区；在完成对
临界资源的访问后再执⾏解锁操作，以释放该临界资源。

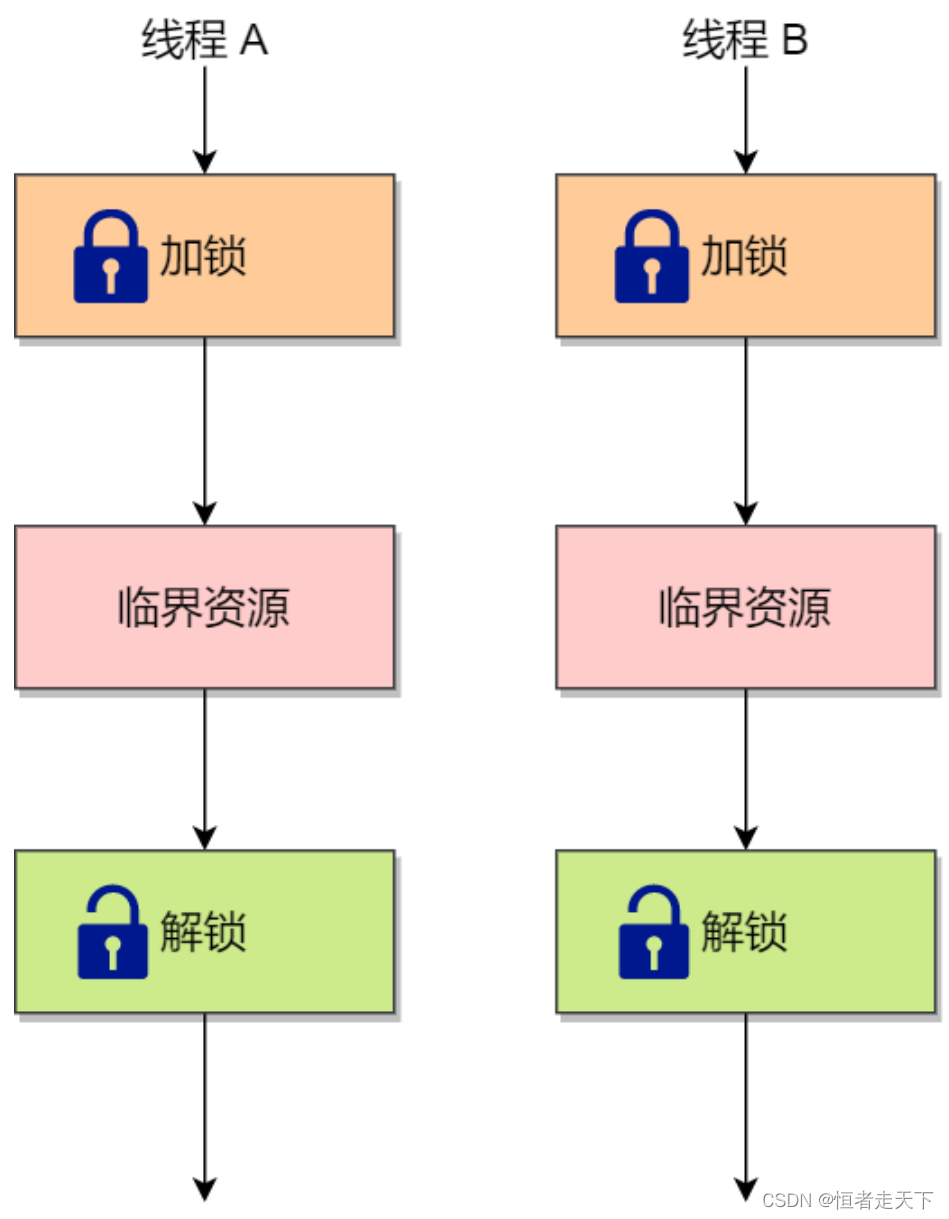
根据锁的实现不同，可以分为「忙等待锁」和「⽆忙等待锁」。

我们先来看看「忙等待锁」的实现
在说明「忙等待锁」的实现之前，先介绍现代 CPU 体系结构提供的特殊原⼦操作指令 —— 测试和置位
（Test-and-Set）指令。

如果⽤ C 代码表示 Test-and-Set 指令，形式如下：

测试并设置指令做了下述事情:

• 把 old_ptr 更新为 new 的新值
• 返回 old_ptr 的旧值；

当然，关键是这些代码是原⼦执⾏。因为既可以测试旧值，⼜可以设置新值，所以我们把这条指令叫作
「测试并设置」。

那什么是原⼦操作呢？原⼦操作就是要么全部执⾏，要么都不执⾏，不能出现执⾏到⼀半的中间状态

我们可以运⽤ Test-and-Set 指令来实现「忙等待锁」，代码如下：

我们来确保理解为什么这个锁能⼯作：

• 第⼀个场景是，⾸先假设⼀个线程在运⾏，调⽤ lock() ，没有其他线程持有锁，所以 flag 是 0。当
  调⽤ TestAndSet(flag, 1) ⽅法，返回 0，线程会跳出 while 循环，获取锁。同时也会原⼦的设置 flag
  为1，标志锁已经被持有。当线程离开临界区，调⽤ unlock() 将 flag 清理为 0。

很明显，当获取不到锁时，线程就会⼀直 wile 循环，不做任何事情，所以就被称为 「忙等待锁」，也被称
为⾃旋锁（spin lock）。

这是最简单的⼀种锁，⼀直⾃旋，利⽤ CPU 周期，直到锁可⽤。在单处理器上，需要抢占式的调度器（即
不断通过时钟中断⼀个线程，运⾏其他线程）。否则，⾃旋锁在单 CPU 上⽆法使⽤，因为⼀个⾃旋的线程
永远不会放弃 CPU。

再来看看「⽆等待锁」的实现
⽆等待锁顾明思议就是获取不到锁的时候，不⽤⾃旋。

既然不想⾃旋，那当没获取到锁的时候，就把当前线程放⼊到锁的等待队列，然后执⾏调度程序，把 CPU
让给其他线程执⾏。

本次只是提出了两种简单锁的实现⽅式。当然，在具体操作系统实现中，会更复杂，但也离不开本例⼦两
个基本元素。

信号量

信号量是操作系统提供的⼀种协调共享资源访问的⽅法。

操作系统是如何实现 PV 操作的呢？
信号量数据结构与 PV 操作的算法描述如下图：

PV 操作的函数是由操作系统管理和实现的，所以操作系统已经使得执⾏ PV 函数时是具有原⼦性的。

⽣产者-消费者问题

⽣产者-消费者问题描述：

• ⽣产者在⽣成数据后，放在⼀个缓冲区中；
• 消费者从缓冲区取出数据处理；
• 任何时刻，只能有⼀个⽣产者或消费者可以访问缓冲区；

我们对问题分析可以得出：

• 任何时刻只能有⼀个线程操作缓冲区，说明操作缓冲区是临界代码，需要互斥；
• 缓冲区空时，消费者必须等待⽣产者⽣成数据；缓冲区满时，⽣产者必须等待消费者取出数据。说明
  ⽣产者和消费者需要同步。

那么我们需要三个信号量，分别是：

• 互斥信号量 mutex ：⽤于互斥访问缓冲区，初始化值为 1；
• 资源信号量 fullBuffers ：⽤于消费者询问缓冲区是否有数据，有数据则读取数据，初始化值为 0
  （表明缓冲区⼀开始为空）；
• 资源信号量 emptyBuffers ：⽤于⽣产者询问缓冲区是否有空位，有空位则⽣成数据，初始化值为 n
  （缓冲区⼤⼩）；

具体的实现代码：

如果消费者线程⼀开始执⾏ P(fullBuffers) ，由于信号量 fullBuffers 初始值为 0，则此时 fullBuffers 的
值从 0 变为 -1，说明缓冲区⾥没有数据，消费者只能等待。

接着，轮到⽣产者执⾏ P(emptyBuffers) ，表示减少 1 个空槽，如果当前没有其他⽣产者线程在临界区执
⾏代码，那么该⽣产者线程就可以把数据放到缓冲区，放完后，执⾏ V(fullBuffers) ，信号量 fullBuffers
从 -1 变成 0，表明有「消费者」线程正在阻塞等待数据，于是阻塞等待的消费者线程会被唤醒。

消费者线程被唤醒后，如果此时没有其他消费者线程在读数据，那么就可以直接进⼊临界区，从缓冲区读
取数据。最后，离开临界区后，把空槽的个数 + 1。

经典同步问题

哲学家就餐问题
来图解这道题

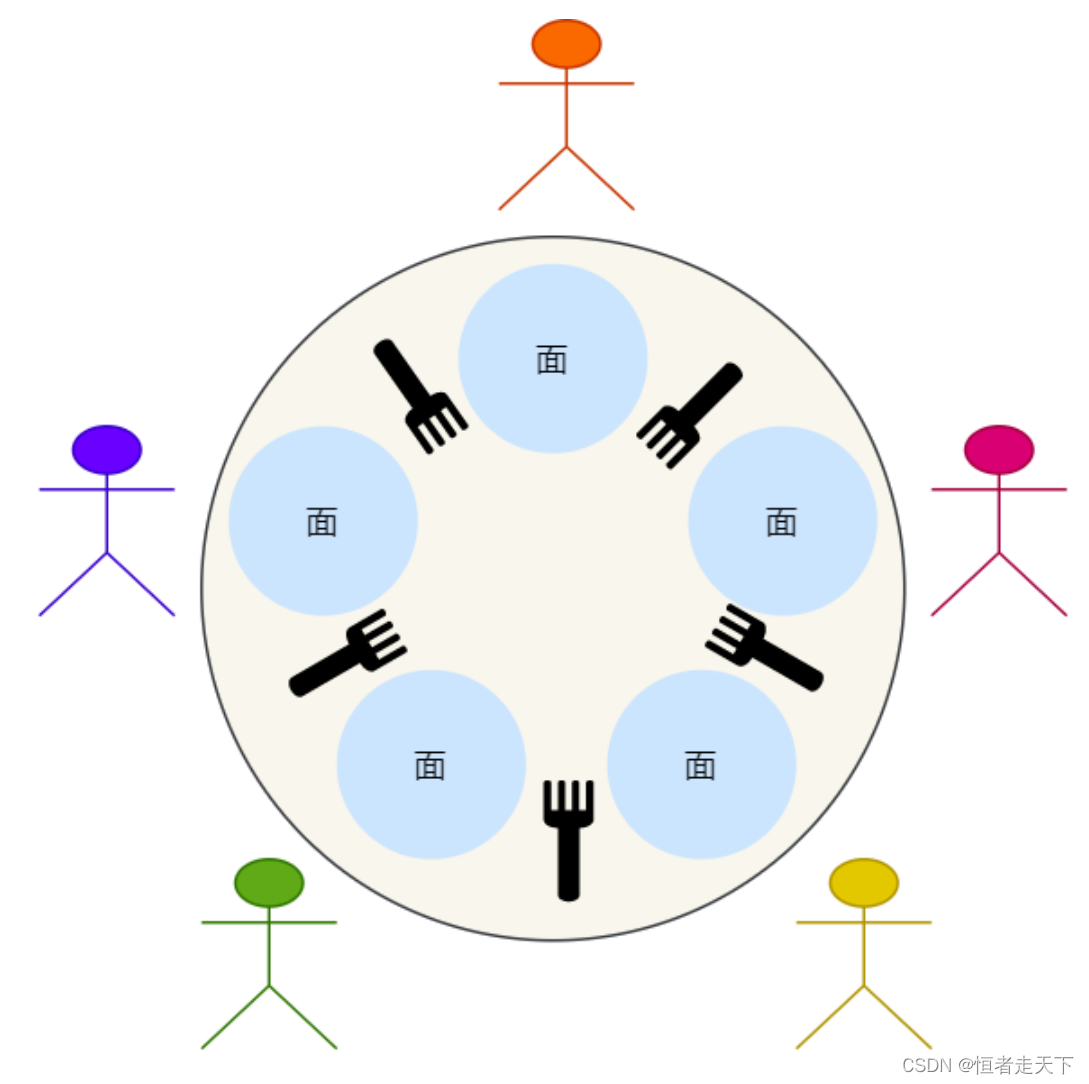
先来看看哲学家就餐的问题描述：

• 5 个⽼⼤哥哲学家，闲着没事做，围绕着⼀张圆桌吃⾯；
• 巧就巧在，这个桌⼦只有 5 ⽀叉⼦，每两个哲学家之间放⼀⽀叉⼦；
• 哲学家围在⼀起先思考，思考中途饿了就会想进餐；
• 奇葩的是，这些哲学家要两⽀叉⼦才愿意吃⾯，也就是需要拿到左右两边的叉⼦才进餐；
• 吃完后，会把两⽀叉⼦放回原处，继续思考；

那么问题来了，如何保证哲 学家们的动作有序进⾏，⽽不会出现有⼈永远拿不到叉⼦呢？

⽅案⼀
我们⽤信号量的⽅式，也就是 PV 操作来尝试解决它，代码如下：

上⾯的程序，好似很⾃然。拿起叉⼦⽤ P 操作，代表有叉⼦就直接⽤，没有叉⼦时就等待其他哲学家放回
叉⼦。

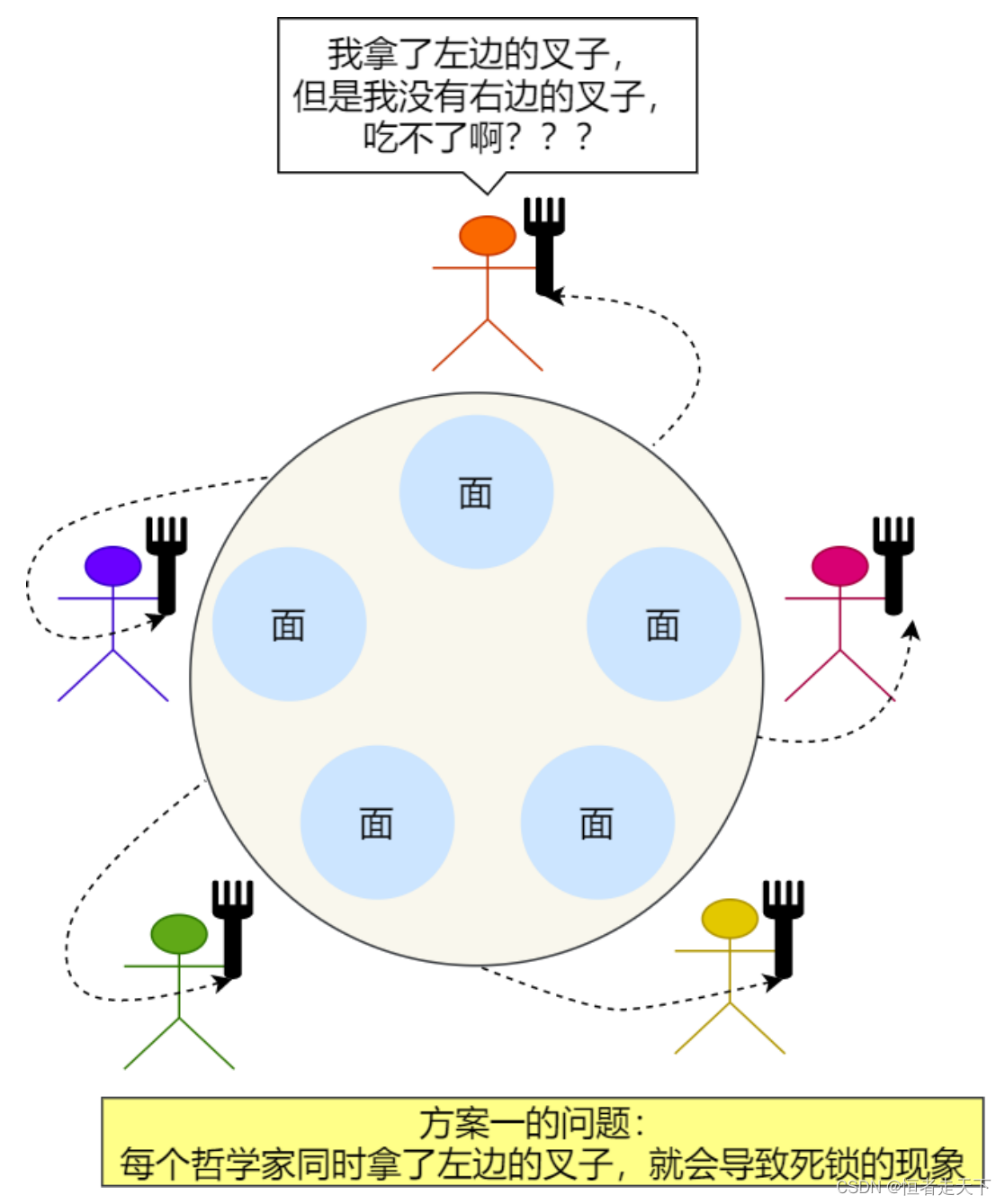
不过，这种解法存在⼀个极端的问题：假设五位哲学家同时拿起左边的叉⼦，桌⾯上就没有叉⼦了，
这样就没有⼈能够拿到他们右边的叉⼦，也就说每⼀位哲学家都会在 P(fork[(i + 1) % N ]) 这条语句阻塞
了，很明显这发⽣了死锁的现象。

⽅案⼆
既然「⽅案⼀」会发⽣同时竞争左边叉⼦导致死锁的现象，那么我们就在拿叉⼦前，加个互斥信号量，代
码如下：

上⾯程序中的互斥信号量的作⽤就在于，只要有⼀个哲学家进⼊了「临界区」，也就是准备要拿叉⼦时，
其他哲学家都不能动，只有这位哲学家⽤完叉⼦了，才能轮到下⼀个哲学家进餐。

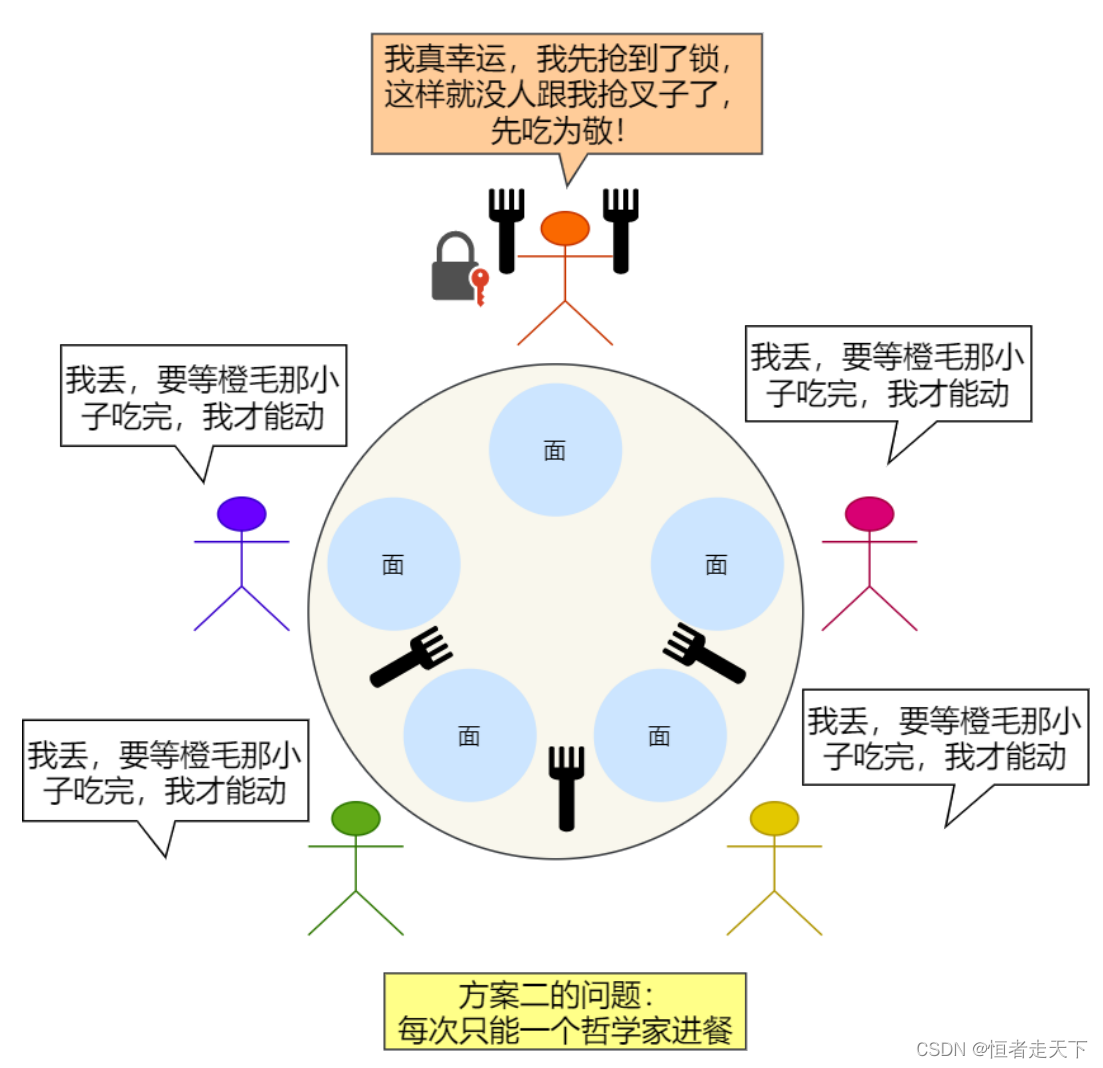
⽅案⼆虽然能让哲学家们按顺序吃饭，但是每次进餐只能有⼀位哲学家，⽽桌⾯上是有 5 把叉⼦，按道理
是能可以有两个哲学家同时进餐的，所以从效率⻆度上，这不是最好的解决⽅案。

⽅案三
那既然⽅案⼆使⽤互斥信号量，会导致只能允许⼀个哲学家就餐，那么我们就不⽤它。

另外，⽅案⼀的问题在于，会出现所有哲学家同时拿左边⼑叉的可能性，那我们就避免哲学家可以同时拿
左边的⼑叉，采⽤分⽀结构，根据哲学家的编号的不同，⽽采取不同的动作。

即让偶数编号的哲学家「先拿左边的叉⼦后拿右边的叉⼦」，奇数编号的哲学家「先拿右边的叉⼦后拿左
边的叉⼦」。

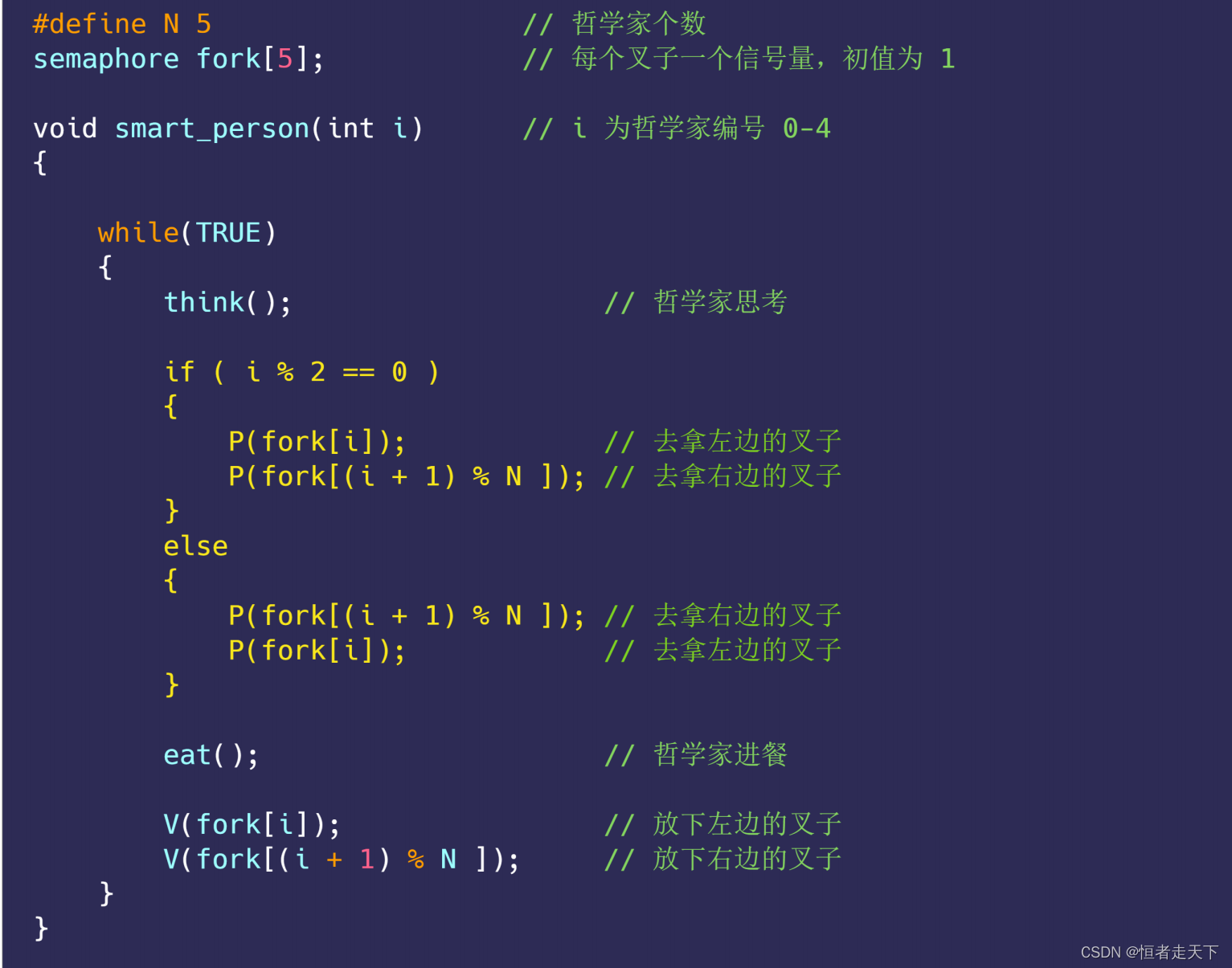
上⾯的程序，在 P 操作时，根据哲学家的编号不同，拿起左右两边叉⼦的顺序不同。另外，V 操作是不需
要分⽀的，因为 V 操作是不会阻塞的。

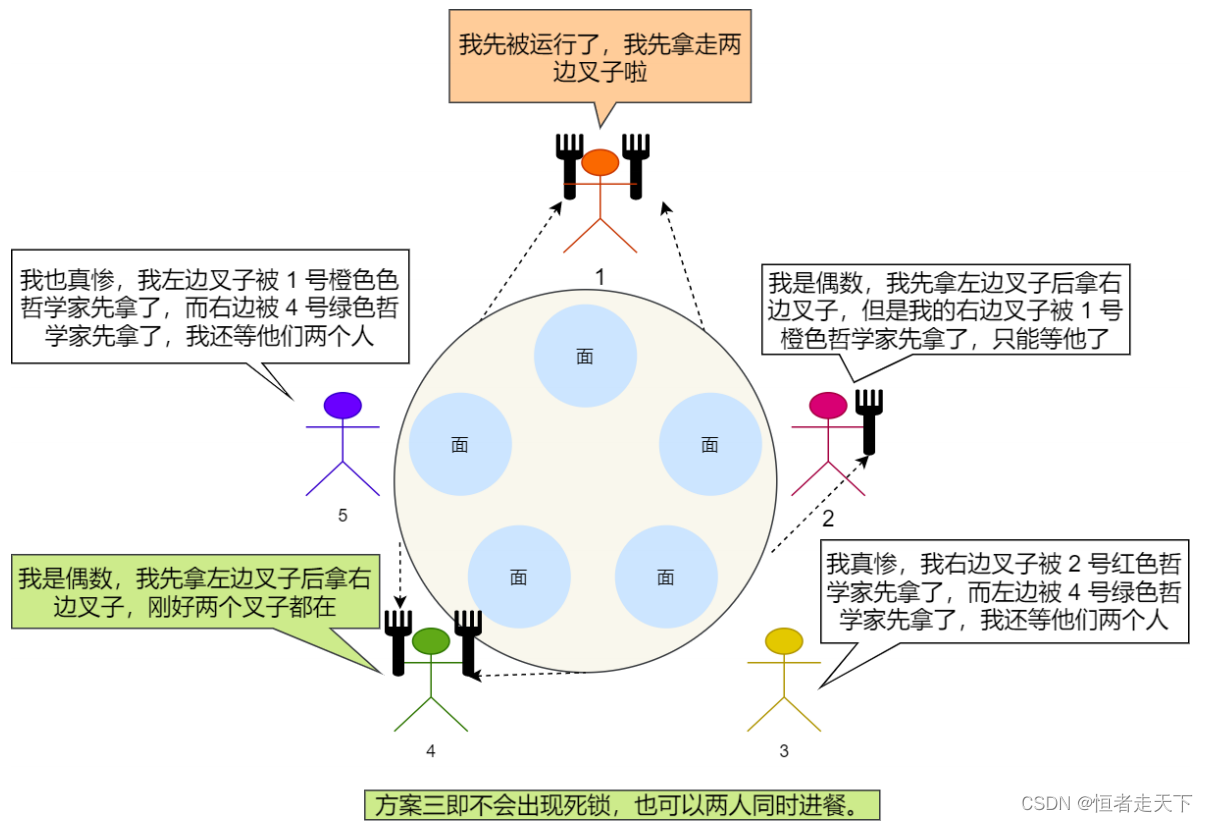
⽅案三即不会出现死锁，也可以两⼈同时进餐。

⽅案四
在这⾥再提出另外⼀种可⾏的解决⽅案，我们⽤⼀个数组 state 来记录每⼀位哲学家在进程、思考还是饥
饿状态（正在试图拿叉⼦）。

那么，⼀个哲学家只有在两个邻居都没有进餐时，才可以进⼊进餐状态。

第 i 个哲学家的左邻右舍，则由宏 LEFT 和 RIGHT 定义：

• LEFT : ( i + 5 - 1 ) % 5
• RIGHT : ( i + 1 ) % 5

⽐如 i 为 2，则 LEFT 为 1， RIGHT 为 3。

读者-写者问题

读者只会读取数据，不会修改数据，⽽写者即可以读也可以修改数据。
读者-写者的问题描述：

• 「读-读」允许：同⼀时刻，允许多个读者同时读
• 「读-写」互斥：没有写者时读者才能读，没有读者时写者才能写
• 「写-写」互斥：没有其他写者时，写者才能写

接下来，提出⼏个解决⽅案来分析分析。

⽅案⼀
使⽤信号量的⽅式来尝试解决：

• 信号量 wMutex ：控制写操作的互斥信号量，初始值为 1 ；
• 读者计数 rCount ：正在进⾏读操作的读者个数，初始化为 0；
• 信号量 rCountMutex ：控制对 rCount 读者计数器的互斥修改，初始值为 1；

接下来看看代码的实现：