题目描述
假设 str1 长度为
N
N
N,str2 长度为
M
M
M,求 str1 和 str2 的最长公共子串。
思路分析
示例:str1 = “12abcd456”, str2 = “7abcd89”,则str1和str2的最长公共子串为 abcd。
注意,子串是连续的。
动态规划解法思路
构建一张dp表,行对应 str1 的位置,列对应 str2 的位置, d p [ i ] [ j ] dp[i][j] dp[i][j] 表示如果必须以 str1 的 i i i 位置结尾,str2的 j j j 位置结尾,最长公共子串是多长。

所以状态转移方程:
d
p
[
i
]
[
j
]
=
{
d
p
[
i
−
1
]
[
j
−
1
]
+
1
if
s
t
r
[
i
]
=
s
t
r
[
j
]
0
if
s
t
r
[
i
]
≠
s
t
r
[
j
]
dp[i][j] = \begin{cases} dp[i-1][j-1] + 1 &\text{if $str[i] = str[j]$}\\ 0 &\text{if $str[i] \ne str[j]$}\\ \end{cases}
dp[i][j]={dp[i−1][j−1]+10if str[i]=str[j]if str[i]=str[j]
整张表中最大值就是最终的最长公共子串的长度,dp表的规模是 O ( N ∗ M ) O(N*M) O(N∗M),所以整体时间复杂度 O ( N ∗ M ) O(N*M) O(N∗M)。
最长公共子串问题是面试常见题目之一,一般在面试场上回答出 O ( N ∗ M ) O(N*M) O(N∗M) 的解法已经是比较优秀了,因为得到 O ( N ∗ M ) O(N*M) O(N∗M) 的解法就已经需要用到动态规划了。但其实这个问题的最优解是 O ( N + M ) O(N+M) O(N+M),需要用到「后缀数组 + height数组」。
后缀数组解法思路
引入一个
h
h
h 数组,下标用
i
n
d
ind
ind 表示,长度与原始数组长度一样,
h
[
i
n
d
]
h[ind]
h[ind] 表示原始数组中以
i
n
d
ind
ind 位置开头的后缀串与它上一个排名的后缀串的最长公共前缀长度。
即
- 先查出来 i n d ind ind 位置开始的后缀串的排名 x x x;
- 然后找到 x − 1 x-1 x−1 名是 j j j 位置开始的后缀串;
- 「 i n d ind ind 位置开头的后缀串」 和 「 j j j 位置开头的后缀串」的「最长公共前缀长度」记录在 h h h 数组中。
问题的关键就在第3步,两个后缀串的最长公共前缀要如何求?如果从头开始比较,则时间复杂度为 O ( N 2 ) O(N^2) O(N2),那么如何优化使得复杂度变成 O ( N ) O(N) O(N)呢?
优化的大体思路在于 h [ i − 1 ] h[i-1] h[i−1] 的值能指导 h [ i ] h[i] h[i] 的值。
首先抛出一个结论:当前位置的答案不会比上一个位置的答案 - 1 差,即 h [ i − 1 ] − 1 ≤ h [ i ] h[i-1]-1 \le h[i] h[i−1]−1≤h[i],如此一来,就不会回退了。
举例说明:

假设17开头的后缀串排名为5,而排名为4的是27开头的后缀串,则 “aaabc” 和 “aaad” 的最长公共前缀为3,所以
h
[
17
]
=
3
h[17] = 3
h[17]=3。
而18位置就是17开头的位置往后挪了一个,所以 h [ 18 ] ≥ h [ 17 ] − 1 h[18] \ge h[17] - 1 h[18]≥h[17]−1,即 h [ 18 ] ≥ 2 h[18] \ge 2 h[18]≥2
可能在计算 h [ 18 ] h[18] h[18] 的时候不是18位置和28位置进行比较,但一定不会比长度 2 小。
假设 18开头的排名为13,要和排名12的进行比较,而排名12的可能是28开头的,也可能不是,但是可以跳过前两个字符,直接从第三个字符开始进行比较。
这里就涉及到了 不回退。
即,计算了 h [ i ] h[i] h[i],就得到了一个右边界值, 到了计算 h [ i + 1 ] h[i+1] h[i+1]时往右边界的左边退一个位置,从该位置开始进行比较。每次只回退一个位置,整体只有 N N N 个位置,所以复杂度是 O ( N ) O(N) O(N)。
h e i g h t height height 数组, h e i g h t [ i ] height[i] height[i] 表示第 i i i 名对应的原始位置和当前排名减1的后缀串的最长公共前缀的长度。
举个例子:
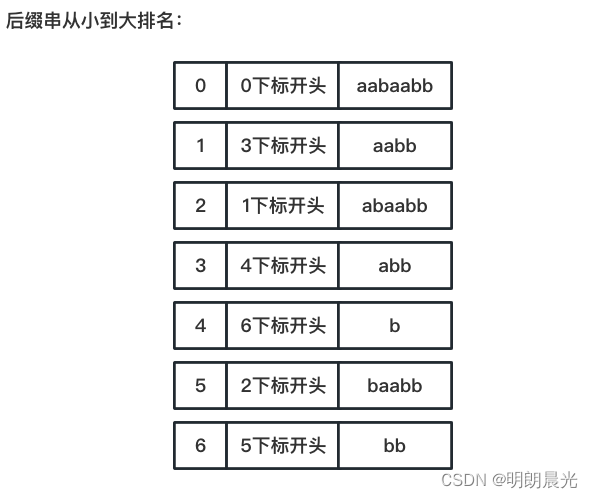
求出
h
h
h 数组:
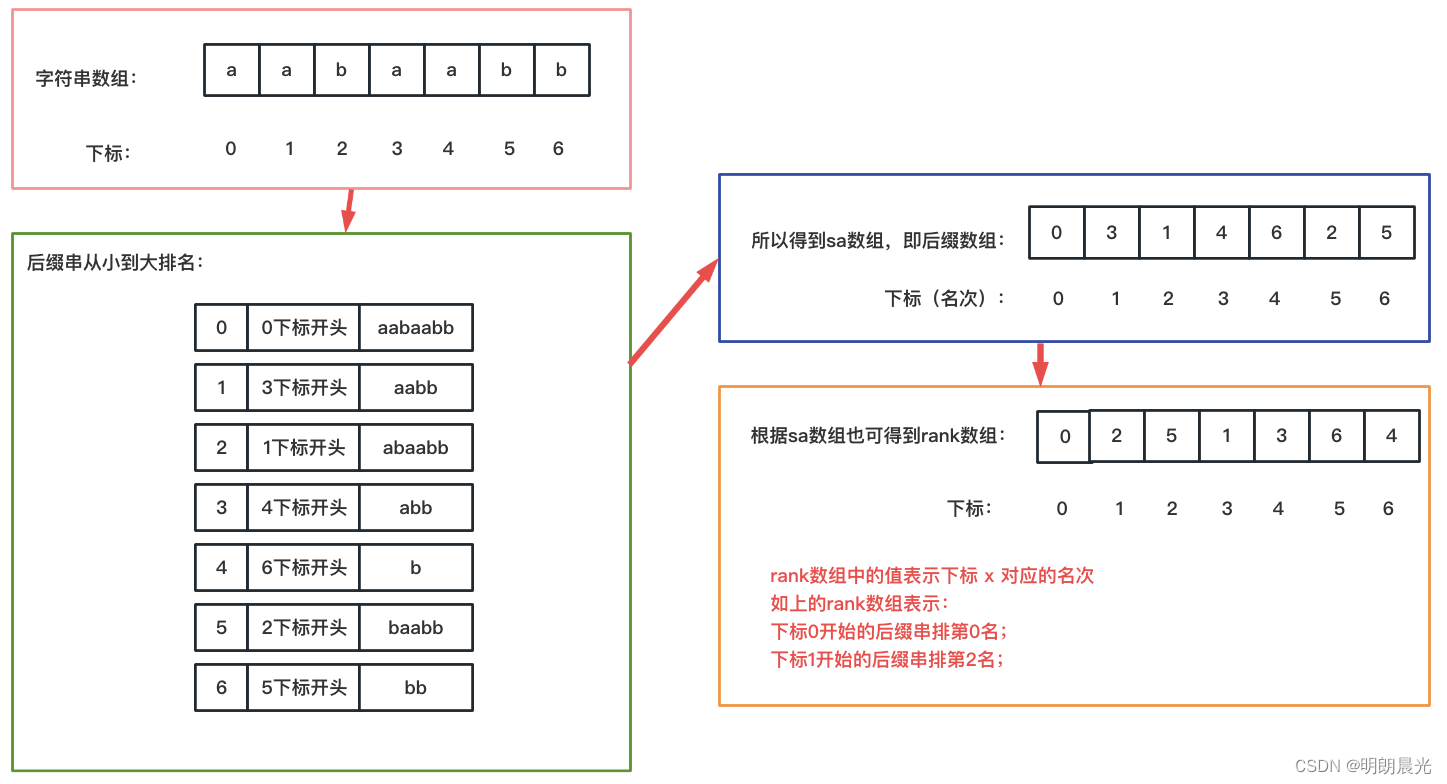
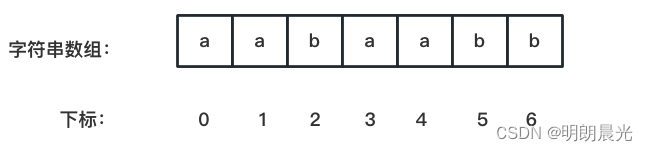
- 原数组 0 位置开始的后缀串 “aabaabb”,它是第0名,没有前一名存在,所以 h [ 0 ] = 0 h[0] = 0 h[0]=0;
- 原数组 1 位置开始的后缀串 “abaabb”,它是第2名,而第1名是3位置开始的后缀串 “aabb”,本来应该依据 h [ 0 ] − 1 = − 1 h[0] -1 = -1 h[0]−1=−1 位置开始比较,这里就有个边界问题了,所以从0位置开始比较, h [ 1 ] = 1 h[1] = 1 h[1]=1;
- 原数组 2 位置开始的后缀串 “baabb”,它是第5名,而第4名是6位置开始的后缀串“b”,于是从后缀串的 h [ 1 ] − 1 = 0 h[1] - 1 = 0 h[1]−1=0 位置开始比较,所以 h [ 2 ] = 1 h[2] = 1 h[2]=1;
- 原数组 3 位置开始的后缀串 “aabb”,它是第1名,和第0名的0位置开始的后缀串“aabaabb” 从 h [ 2 ] − 1 = 0 h[2] - 1 = 0 h[2]−1=0 位置开始比较,得到结果为 h [ 3 ] = 3 h[3] = 3 h[3]=3;
- 原数组 4 位置开始的后缀串 “abb”,它是第3名,和第2名的1位置开始的后缀串"abaabb" 从 h [ 3 ] − 1 = 2 h[3] - 1 = 2 h[3]−1=2 位置开始比较,发现 “abb” 的2位置的 b 和 "abaabb"的2位置的 a 不相同,所以 h [ 4 ] = 2 h[4] = 2 h[4]=2;
- 原数组 5 位置开始的后缀串“bb”,它是第6名,和第5名的2位置开始的后缀串"baabb" 从 h [ 4 ] − 1 = 1 h[4] - 1 = 1 h[4]−1=1 位置开始比较,b ≠ a,所以 h [ 5 ] = 1 h[5] = 1 h[5]=1;
- 原数组 6 位置开始的后缀串"b",它是第4名,和第3名的4位置开始的后缀串“abb” 从 h [ 5 ] − 1 = 0 h[5] - 1 = 0 h[5]−1=0 位置开始比较,b ≠ a,所以 h [ 6 ] = 0 h[6] = 0 h[6]=0。
所以 h = [ 0 , 1 , 1 , 3 , 2 , 1 , 0 ] h=[0, 1, 1, 3, 2, 1, 0] h=[0,1,1,3,2,1,0],对于整个字符串来说,比较的过程中是不回退的。
通过 h h h 数组可以得到 h e i g h t height height 数组。
- 第0名的是0开头的,于是将 h [ 0 ] h[0] h[0] 填入到 h e i g h t [ 0 ] height[0] height[0] 中,所以 h e i g h t [ 0 ] = h [ 0 ] = 0 height[0] = h[0] = 0 height[0]=h[0]=0;
- 第1名的是3开头的,于是将 h [ 3 ] h[3] h[3] 填入到 h e i g h t [ 1 ] height[1] height[1]中,所以 h e i g h t [ 1 ] = h [ 3 ] = 3 height[1] = h[3] = 3 height[1]=h[3]=3;
- 第2名的是1开头的,于是将 h [ 1 ] h[1] h[1] 填入到 h e i g h t [ 2 ] height[2] height[2]中,所以 h e i g h t [ 2 ] = h [ 1 ] = 1 height[2] = h[1] = 1 height[2]=h[1]=1;
- 第3名的是4开头的,于是将 h [ 4 ] h[4] h[4] 填入到 h e i g h t [ 3 ] height[3] height[3]中,所以 h e i g h t [ 3 ] = h [ 4 ] = 2 height[3] = h[4] = 2 height[3]=h[4]=2;
- 第4名的是6开头的,于是将 h [ 6 ] h[6] h[6] 填入到 h e i g h t [ 4 ] height[4] height[4]中,所以 h e i g h t [ 4 ] = h [ 6 ] = 0 height[4] = h[6] = 0 height[4]=h[6]=0;
- 第5名的是2开头的,于是将 h [ 2 ] h[2] h[2] 填入到 h e i g h t [ 5 ] height[5] height[5]中,所以 h e i g h t [ 5 ] = h [ 2 ] = 1 height[5] = h[2] = 1 height[5]=h[2]=1;
- 第6名的是5开头的,于是将 h [ 5 ] h[5] h[5] 填入到 h e i g h t [ 6 ] height[6] height[6]中,所以 h e i g h t [ 6 ] = h [ 5 ] = 1 height[6] = h[5] = 1 height[6]=h[5]=1;
所以 h e i g h t = [ 0 , 3 , 1 , 2 , 0 , 1 , 1 ] height = [0, 3, 1, 2, 0, 1, 1] height=[0,3,1,2,0,1,1]。
h
h
h 数组的位置下标对应的是原数组的每个位置下标,讨论的是和上一个名次的公共前缀;
h
e
i
g
h
t
height
height 数组的位置下标表示的是名次,讨论的是第
i
i
i 名的后缀串的开始位置和它排名最接近的后缀串的公共前缀
通过 h h h 数组遍历一遍就能生成 h e i g h t height height 数组。
h e i g h t [ i ] height[i] height[i] 的含义:其中 i i i 表示名次,通过 s a sa sa 数组找到排第 i i i 名的后缀串的开始位置 s a [ i ] = x sa[i] = x sa[i]=x 和 排第 i − 1 i-1 i−1 名的后缀串的开始位置 s a [ i − 1 ] = y sa[i-1] = y sa[i−1]=y,找到 x x x 开始的后缀串和 y y y 开始的后缀串的最长公共前缀。
用途:如果两个字符串有最长公共子串,如 str1 = “12abcd34” 和 str2 = “4567abcd89”,那么 str1 的2位置开头的后缀串的排名和 str2 的4位置开头的后缀串的排名一定是挨着的。
所以整体流程就是:
- 先将 str1 和 str2 合成一个数组 “str1 + 最小的ASCII码 + str2”,即 arr = “12abcd3404567abcd89”;
- 然后对这个数组求解 s a 、 r a n k 、 h e i g h t sa、rank、height sa、rank、height 数组;
- 接着考察
h
e
i
g
h
t
height
height 数组中的值;
假设来到 h e i g h t height height 数组的 i i i 位置,通过 s a sa sa 数组查出了它对应的后缀串的开始位置为 x,而它的前一名 i − 1 i-1 i−1 对应的后缀串的开始位置为 y y y,如果 x x x 和 y y y 位于 arr 数组的最小ASCII码的两侧,表示来自原始串的两个不同串,记录下此时的 h e i g h t [ i ] height[i] height[i],所有符合来自左右两侧的 h e i g h t height height 数组的值就是达标的,否则不达标。 - 最后在所有达标的 h e i g h t height height 数组中的值求最大值,就是最长共子串长度。
代码实现
// 最长公共子串问题是面试常见题目之一
// 假设str1长度N,str2长度M
// 因为最优解的难度所限,一般在面试场上回答出O(N*M)的解法已经是比较优秀了
// 因为得到O(N*M)的解法,就已经需要用到动态规划了
// 但其实这个问题的最优解是O(N+M),为了达到这个复杂度可是不容易
// 首先需要用到DC3算法得到后缀数组(sa)
// 进而用sa数组去生成height数组
// 而且在生成的时候,还有一个不回退的优化,都非常不容易理解
// 这就是后缀数组在面试算法中的地位 : 德高望重的噩梦
public class LongestCommonSubstringConquerByHeight {
//动态规划的解法,还用了空间压缩
//时间复杂度 O(N*M)
public static int lcs1(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int row = 0;
int col = str2.length - 1;
int max = 0;
while (row < str1.length) {
int i = row;
int j = col;
int len = 0;
while (i < str1.length && j < str2.length) {
if (str1[i] != str2[j]) {
len = 0;
} else {
len++;
}
if (len > max) {
max = len;
}
i++;
j++;
}
if (col > 0) {
col--;
} else {
row++;
}
}
return max;
}
// 后缀数组的解法:O(N)
public static int lcs2(String s1, String s2) {
if (s1 == null || s2 == null || s1.length() == 0 || s2.length() == 0) {
return 0;
}
//1. 两个数组合成一个数组
char[] str1 = s1.toCharArray();
char[] str2 = s2.toCharArray();
int N = str1.length;
int M = str2.length;
int min = str1[0];
int max = str1[0];
for (int i = 1; i < N; i++) {
min = Math.min(min, str1[i]);
max = Math.max(max, str1[i]);
}
for (int i = 0; i < M; i++) {
min = Math.min(min, str2[i]);
max = Math.max(max, str2[i]);
}
int[] all = new int[N + M + 1];
int index = 0;
for (int i = 0; i < N; i++) {
all[index++] = str1[i] - min + 2;
}
all[index++] = 1;
for (int i = 0; i < M; i++) {
all[index++] = str2[i] - min + 2;
}
// 2. 调用DC3算法求解sa、rank 和 height数组
DC3 dc3 = new DC3(all, max - min + 2);
// 3. 利用高度数组求解最长公共子串
int n = all.length;
int[] sa = dc3.sa;
int[] height = dc3.height;
int ans = 0;
for (int i = 1; i < n; i++) {
int Y = sa[i - 1]; //排第i-1名的后缀串的开始位置
int X = sa[i]; //排第i名的后缀串的开始位置
if (Math.min(X, Y) < N && Math.max(X, Y) > N) { //判断x和y是否来自all数组的最小ASCII码的左右两侧
ans = Math.max(ans, height[i]);
}
}
return ans;
}
public static class DC3 {
public int[] sa;
public int[] rank;
public int[] height;
public DC3(int[] nums, int max) {
sa = sa(nums, max);
rank = rank();
height = height(nums);
}
private int[] sa(int[] nums, int max) {
int n = nums.length;
int[] arr = new int[n + 3];
for (int i = 0; i < n; i++) {
arr[i] = nums[i];
}
return skew(arr, n, max);
}
private int[] skew(int[] nums, int n, int K) {
int n0 = (n + 2) / 3, n1 = (n + 1) / 3, n2 = n / 3, n02 = n0 + n2;
int[] s12 = new int[n02 + 3], sa12 = new int[n02 + 3];
for (int i = 0, j = 0; i < n + (n0 - n1); ++i) {
if (0 != i % 3) {
s12[j++] = i;
}
}
radixPass(nums, s12, sa12, 2, n02, K);
radixPass(nums, sa12, s12, 1, n02, K);
radixPass(nums, s12, sa12, 0, n02, K);
int name = 0, c0 = -1, c1 = -1, c2 = -1;
for (int i = 0; i < n02; ++i) {
if (c0 != nums[sa12[i]] || c1 != nums[sa12[i] + 1] || c2 != nums[sa12[i] + 2]) {
name++;
c0 = nums[sa12[i]];
c1 = nums[sa12[i] + 1];
c2 = nums[sa12[i] + 2];
}
if (1 == sa12[i] % 3) {
s12[sa12[i] / 3] = name;
} else {
s12[sa12[i] / 3 + n0] = name;
}
}
if (name < n02) {
sa12 = skew(s12, n02, name);
for (int i = 0; i < n02; i++) {
s12[sa12[i]] = i + 1;
}
} else {
for (int i = 0; i < n02; i++) {
sa12[s12[i] - 1] = i;
}
}
int[] s0 = new int[n0], sa0 = new int[n0];
for (int i = 0, j = 0; i < n02; i++) {
if (sa12[i] < n0) {
s0[j++] = 3 * sa12[i];
}
}
radixPass(nums, s0, sa0, 0, n0, K);
int[] sa = new int[n];
for (int p = 0, t = n0 - n1, k = 0; k < n; k++) {
int i = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
int j = sa0[p];
if (sa12[t] < n0 ? leq(nums[i], s12[sa12[t] + n0], nums[j], s12[j / 3])
: leq(nums[i], nums[i + 1], s12[sa12[t] - n0 + 1], nums[j], nums[j + 1], s12[j / 3 + n0])) {
sa[k] = i;
t++;
if (t == n02) {
for (k++; p < n0; p++, k++) {
sa[k] = sa0[p];
}
}
} else {
sa[k] = j;
p++;
if (p == n0) {
for (k++; t < n02; t++, k++) {
sa[k] = sa12[t] < n0 ? sa12[t] * 3 + 1 : (sa12[t] - n0) * 3 + 2;
}
}
}
}
return sa;
}
private void radixPass(int[] nums, int[] input, int[] output, int offset, int n, int k) {
int[] cnt = new int[k + 1];
for (int i = 0; i < n; ++i) {
cnt[nums[input[i] + offset]]++;
}
for (int i = 0, sum = 0; i < cnt.length; ++i) {
int t = cnt[i];
cnt[i] = sum;
sum += t;
}
for (int i = 0; i < n; ++i) {
output[cnt[nums[input[i] + offset]]++] = input[i];
}
}
private boolean leq(int a1, int a2, int b1, int b2) {
return a1 < b1 || (a1 == b1 && a2 <= b2);
}
private boolean leq(int a1, int a2, int a3, int b1, int b2, int b3) {
return a1 < b1 || (a1 == b1 && leq(a2, a3, b2, b3));
}
//生成rank数组
private int[] rank() {
int n = sa.length;
int[] ans = new int[n];
for (int i = 0; i < n; i++) {
ans[sa[i]] = i;
}
return ans;
}
// 生成height数组
private int[] height(int[] s) {
int n = s.length;
int[] ans = new int[n];
// 因为求解 h[i] 只需要 h[i-1] 的值,所以不需要数组,用一个变量k滚动即可
// 依次求h[i] , 一开始最长公共前缀为0,所以 k = 0
for (int i = 0, k = 0; i < n; ++i) {
if (rank[i] != 0) { //只要不是第0名,就要去求最长公共前缀
if (k > 0) {
--k;
}
int j = sa[rank[i] - 1];
//枚举的过程,两个后缀串从第 k-1 个位置开始比较,如果相等则++,不等则结束循环
while (i + k < n && j + k < n && s[i + k] == s[j + k]) {
++k;
}
// 此时的 h[i] = k
ans[rank[i]] = k;
}
}
return ans;
}
}
// for test
public static String randomNumberString(int len, int range) {
char[] str = new char[len];
for (int i = 0; i < len; i++) {
str[i] = (char) ((int) (Math.random() * range) + 'a');
}
return String.valueOf(str);
}
public static void main(String[] args) {
int len = 30;
int range = 5;
int testTime = 100000;
System.out.println("功能测试开始");
for (int i = 0; i < testTime; i++) {
int N1 = (int) (Math.random() * len);
int N2 = (int) (Math.random() * len);
String str1 = randomNumberString(N1, range);
String str2 = randomNumberString(N2, range);
int ans1 = lcs1(str1, str2);
int ans2 = lcs2(str1, str2);
if (ans1 != ans2) {
System.out.println("Oops!");
}
}
System.out.println("功能测试结束");
System.out.println("==========");
System.out.println("性能测试开始");
len = 80000;
range = 26;
long start;
long end;
String str1 = randomNumberString(len, range);
String str2 = randomNumberString(len, range);
start = System.currentTimeMillis();
int ans1 = lcs1(str1, str2);
end = System.currentTimeMillis();
System.out.println("方法1结果 : " + ans1 + " , 运行时间 : " + (end - start) + " ms");
start = System.currentTimeMillis();
int ans2 = lcs2(str1, str2);
end = System.currentTimeMillis();
System.out.println("方法2结果 : " + ans2 + " , 运行时间 : " + (end - start) + " ms");
System.out.println("性能测试结束");
}
}