时间复杂度
①what:
指执行当前算法所消耗的时间
②简介结论:
时间复杂度由多项式T(n)中最高阶的项来决定,系数的影响忽略即可
例子:
| 操作数量T(n) | 时间复杂度O(f(n)) |
| 常数,比如 100000(即:n的0次方 值为1) | O(1) |
| 一次函数,比如 3n+2 | O(n) |
| 二次函数,比如 2n^2+3n+2 | O(n^2) |
| 三次函数,比如 n^3+10000n^2 | O(n^3) |
| ... | 以此类推 |
| 2^n+10000n^10000 2^n从某个位置开始会出现“爆炸性”增长,指数增长幅度远大于幂增长 | O(2^n) |
③常见类型:
设输入数据大小为n,常见的时间复杂度类型(从低到高)有:
O(1)<O(logn) < O(n) < O(nlogn) < O(n^2)< O(2^n)<O(n!)
对应:常数阶< 对数阶 <线性阶<线性对数阶<平方阶 < 指数阶 <阶乘阶
----说明:这里logn也就是log2 n (2为下标)

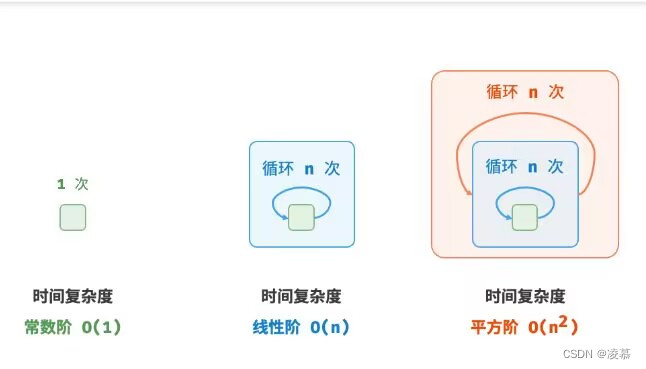
- 常数阶O(1)
常数阶的操作数量与输入数据大小n无关,即不随着n的变化而变化
无论操作数量size有多大,只要与数据大小n无关,时间复杂度就仍为O(1)
/* 常数阶 O(1) */
int constant(int n){
int cnt=0;
int size=100000;
for(int i=0;i<size;i++) cnt++;
return cnt;
} - 对数阶O(logn)
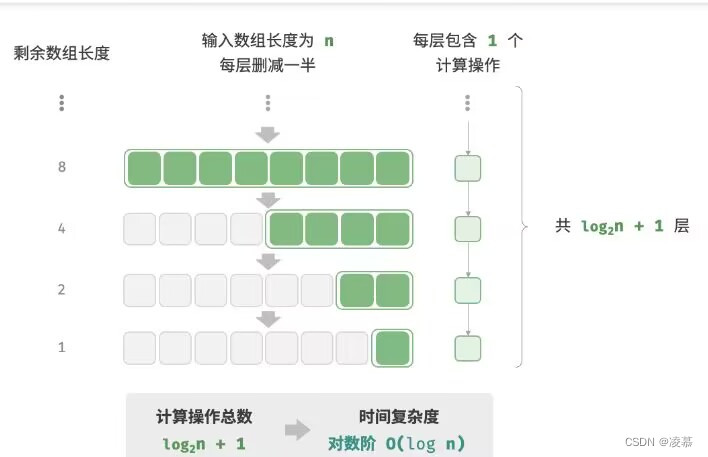
对数阶反映“每轮缩减到一半的情况”
对数阶常出现于「二分查找」和「分治算法」中,体现“一分为多”、“化繁为简”的算法思想
现在:设输入数据大小为n,由于每轮缩减到一半,因此循环次数是log2^n
/* 对数阶 O(logn) */
int logarithmic(float n){
int cnt=0;
while(n>1) n/=2,cnt++;
return cnt;
} 
对数阶也常出现于递归函数,代码如下:
/* 对数阶(递归实现) */
int logRecur(float n){
if(n<=1) return 0;
return logRecur(n/2)+1;
} - 线性阶O(n)
线性阶的操作数量相对输入数据大小成线性级别增长,常出现在单层循环
/* 线性阶 O(n) */
int linear(int n){
int cnt=0;
for(int i=0;i<n;i++) cnt++;
return cnt;
} 涨知识:「遍历数组」和「遍历链表」等操作,时间复杂度都为O(n),其中n为数组或链表的长度。
- 线性对数阶O(nlogn)
线性对数阶常出现于嵌套循环中,两层循环的时间复杂度分别为O(logn)和O(n)
主流排序算法的时间复杂度都是O(nlogn),例如快速排序、归并排序、堆排序等
/* 线性对数阶 O(nlogn) */
int linearLogRecur(float n){
if(n<=1) return 1;
int cnt=linearLogRecur(n/2)+linearLogRecur(n/2);
for(int i=0;i<n;i++) cnt++;
return cnt;
} - 平方阶O(n²)
平方阶常出现于嵌套循环,外层循环和内层循环都为O(n),总体为O(n2)
- 指数阶O(2^n)
借用“细胞分裂”来代表指数阶增长:初始状态为1个细胞,分裂一轮后为2个,分裂两轮后为4个,....分裂n轮后为2^n个细胞,指数阶常出现于递归函数
/* 指数阶 O(2^n) */
int exponential(int n){
int cnt=0,base=1;
// cell每轮一分为二,形成数列 1,2,4,8,... ,2^(n-1)
for(int i=0;i<n;i++)
for(int j=0;j<base;j++)
cnt++;
base*=2;
return cnt;
} - 阶乘阶 O(n!)
阶乘阶对应数学上的「全排列」
即给定n个互不重复的元素,求其所有可能的排列方案,则方案数量为
n!=n*(n-1)*(n- 2)*...*2*1
阶乘常使用递归实现
例如以下代码,第一层分裂出n个,第二层分裂出n-1个,....,直至到第n层时终止分裂
/* 阶乘阶 O(n!) */
int factorialRecur(int n){
if(n==0) return 1;
int cnt=0;
//从 1个分裂出 n个
for(int i=0;i<n;i++) cnt+=factorialRecur(n-1);
return cnt;
} 完 //总结:站在巨人的肩膀上打小抄