LC-1041 困于环中的机器人（模拟，快慢指针找环）

1041. 困于环中的机器人

难度中等148

在无限的平面上，机器人最初位于 (0, 0) 处，面朝北方。注意:

北方向 是y轴的正方向。
南方向 是y轴的负方向。
东方向 是x轴的正方向。
西方向 是x轴的负方向。

机器人可以接受下列三条指令之一：

"G"：直走 1 个单位
"L"：左转 90 度
"R"：右转 90 度

机器人按顺序执行指令 instructions，并一直重复它们。

只有在平面中存在环使得机器人永远无法离开时，返回 true。否则，返回 false。

示例 1：

输入：instructions = "GGLLGG"
输出：true
解释：机器人最初在(0,0)处，面向北方。
“G”:移动一步。位置:(0,1)方向:北。
“G”:移动一步。位置:(0,2).方向:北。
“L”:逆时针旋转90度。位置:(0,2).方向:西。
“L”:逆时针旋转90度。位置:(0,2)方向:南。
“G”:移动一步。位置:(0,1)方向:南。
“G”:移动一步。位置:(0,0)方向:南。
重复指令，机器人进入循环:(0,0)——>(0,1)——>(0,2)——>(0,1)——>(0,0)。
在此基础上，我们返回true。

示例 2：

输入：instructions = "GG"
输出：false
解释：机器人最初在(0,0)处，面向北方。
“G”:移动一步。位置:(0,1)方向:北。
“G”:移动一步。位置:(0,2).方向:北。
重复这些指示，继续朝北前进，不会进入循环。
在此基础上，返回false。

示例 3：

输入：instructions = "GL"
输出：true
解释：机器人最初在(0,0)处，面向北方。
“G”:移动一步。位置:(0,1)方向:北。
“L”:逆时针旋转90度。位置:(0,1).方向:西。
“G”:移动一步。位置:(- 1,1)方向:西。
“L”:逆时针旋转90度。位置:(- 1,1)方向:南。
“G”:移动一步。位置:(- 1,0)方向:南。
“L”:逆时针旋转90度。位置:(- 1,0)方向:东方。
“G”:移动一步。位置:(0,0)方向:东方。
“L”:逆时针旋转90度。位置:(0,0)方向:北。
重复指令，机器人进入循环:(0,0)——>(0,1)——>(- 1,1)——>(- 1,0)——>(0,0)。
在此基础上，我们返回true。

提示：

1 <= instructions.length <= 100
instructions[i] 仅包含 'G', 'L', 'R'

找规律模拟

【四次归零】题解：https://leetcode.cn/problems/robot-bounded-in-circle/solution/python3-si-ci-gui-ling-kun-yu-huan-zhong-5l1k/

看到这道题，首先想到的应该是202.快乐数这道题，在202题中，可以设置一个阈值 7次，如果7次后仍旧不快乐，那就永远都不会快乐了。

既然本题也是找是否成环，那不如同样的思路也来想想是否会存在一个类似的阈值。

随便试几个例子不难想到，示例三给出的例子是最极端的例子。

所以我们可以得出一个结论：

如果机器人被困于环内，那么机器人一定会在一次、两次、四次循环的最后走到原点(0, 0)。

若四次还没有走到原点，那么机器人一定不会被困于环中。

class Solution {
    public boolean isRobotBounded(String instructions) {
        int n = instructions.length();
        int x = 0, y = 0;
        int d = 0; // 方向 0123 -> 上右下左
        for(int i = 0; i < n*4; i++){
            char c = instructions.charAt(i % n);
            if(c == 'R') d = (d+1 + 4) % 4; // 右转
            if(c == 'L') d = (d-1 + 4) % 4; // 左转
            if(c == 'G'){
                if(d == 0) y += 1;
                else if(d == 1) x += 1;
                else if(d == 2) y -= 1;
                else x -= 1;
            }
            if(x == 0 && y == 0 && i % n == n-1){
                return true;
            }
        }
        return false;
    }
}

202. 快乐数

难度简单1278

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

提示：

1 <= n <= 231 - 1

判断循环就用快慢指针

https://leetcode.cn/problems/happy-number/solution/shi-yong-kuai-man-zhi-zhen-si-xiang-zhao-chu-xun-h/

使用 “快慢指针” 思想，找出循环：“快指针” 每次走两步，“慢指针” 每次走一步，当二者相等时，即为一个循环周期。此时，判断是不是因为 1 引起的循环，是的话就是快乐数，否则不是快乐数。

注意：此题不建议用集合记录每次的计算结果来判断是否进入循环，因为这个集合可能大到无法存储；另外，也不建议使用递归，同理，如果递归层次较深，会直接导致调用栈崩溃。不要因为这个题目给出的整数是 int 型而投机取巧。

class Solution {
    public boolean isHappy(int n) {
        int slow = n, fast = n;
        do{
            slow = bitSquareSum(slow);
            fast = bitSquareSum(fast);
            fast = bitSquareSum(fast);
        }while(slow != fast);
        return slow == 1;
    }

    public int bitSquareSum(int n){
        int sum = 0;
        while(n != 0){
            sum += Math.pow(n%10, 2);
            n = n / 10;
        }
        return sum;
    }
}

哈希表

用哈希表来标记寻找快乐数的过程中出现的数，如果有的数重复出现则表示已经进入死循环

class Solution {
    public boolean isHappy(int n) {
        Set<Integer> set = new HashSet<>();
        while(n != 1 && !set.contains(n)){
            set.add(n);
            n = bitSquareSum(n);
        }
        return n == 1;
    }

    public int bitSquareSum(int n){
        int sum = 0;
        while(n != 0){
            sum += Math.pow(n%10, 2);
            n = n / 10;
        }
        return sum;
    }
}

287. 寻找重复数

难度中等2112

给定一个包含 n + 1 个整数的数组 nums ，其数字都在 [1, n] 范围内（包括 1 和 n），可知至少存在一个重复的整数。

假设 nums 只有 一个重复的整数 ，返回 这个重复的数 。

你设计的解决方案必须 不修改 数组 nums 且只用常量级 O(1) 的额外空间。

示例 1：

输入：nums = [1,3,4,2,2]
输出：2

示例 2：

输入：nums = [3,1,3,4,2]
输出：3

提示：

1 <= n <= 105
nums.length == n + 1
1 <= nums[i] <= n
nums 中 只有一个整数 出现 两次或多次 ，其余整数均只出现一次

进阶：

如何证明 nums 中至少存在一个重复的数字?
你可以设计一个线性级时间复杂度 O(n) 的解决方案吗？

快慢指针

https://leetcode.cn/problems/find-the-duplicate-number/solution/kuai-man-zhi-zhen-de-jie-shi-cong-damien_undoxie-d/

将这个题目给的特殊的数组当作一个链表来看，数组的下标就是指向元素的指针，把数组的元素也看作指针。如 0 是指针，指向 nums[0]，而 nums[0] 也是指针，指向 nums[nums[0]].

这样我们就可以有这样的操作

int point = 0;
while(true){
    point = nums[point]; // 等同于 next = next->next; 
}

链表中的环

假设有这样一个样例：[1,2,3,4,5,6,7,8,9,5]。如果我们按照上面的循环下去就会得到这样一个路径：1 2 3 4 5 [6 7 8 9] [6 7 8 9] [6 7 8 9] . . .这样就有了一个环，也就是 6 7 8 9。point 会一直在环中循环的前进。

这时我们设置两个一快(fast)一慢(slow)两个指针，一个每次走两步，一个每次走一步，这样让他们一直走下去，直到他们在重复的序列中相遇，

int fast = 0, slow = 0;
while(true){
    fast = nums[nums[fast]];
    slow = nums[slow];
    if(fast == slow)
        break;
}

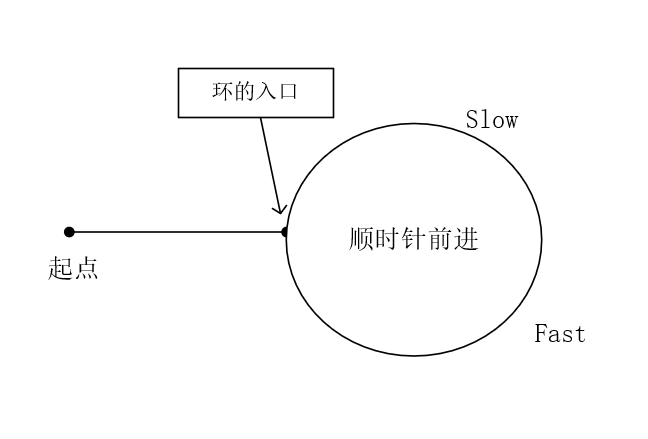
如上图，slow 和 fast 会在环中相遇，先假设一些量：起点到环的入口长度为 m，环的周长为 c，在 fast 和 slow 相遇时 slow 走了 n 步。则 fast 走了 2n 步，fast 比 slow 多走了 n 步，而这 n 步全用在了在环里循环（n%c==0）。

当 fast 和 last 相遇之后，我们设置第三个指针 finder，它从起点开始和 slow(在 fast 和 slow 相遇处)同步前进，当 finder 和 slow 相遇时，就是在环的入口处相遇，也就是重复的那个数字相遇。

为什么 finder 和 slow 相遇在入口

fast 和 slow 相遇时，slow 在环中行进的距离是 n-m，其中 n%c==0。这时我们再让 slow 前进 m 步——也就是在环中走了 n 步了。而 n%c==0 即 slow 在环里面走的距离是环的周长的整数倍，就回到了环的入口了，而入口就是重复的数字。

我们不知道起点到入口的长度 m，所以弄个 finder 和 slow 一起走，他们必定会在入口处相遇。

class Solution {
    public int findDuplicate(int[] nums) {
        int fast = 0, slow = 0;
        while(true){
            fast = nums[nums[fast]];
            slow = nums[slow];
            if(fast == slow) break;
        }
        int finder = 0;
        while(true){
            finder = nums[finder];
            slow = nums[slow];
            if(slow == finder) break;
        }
        return slow;
    }
}