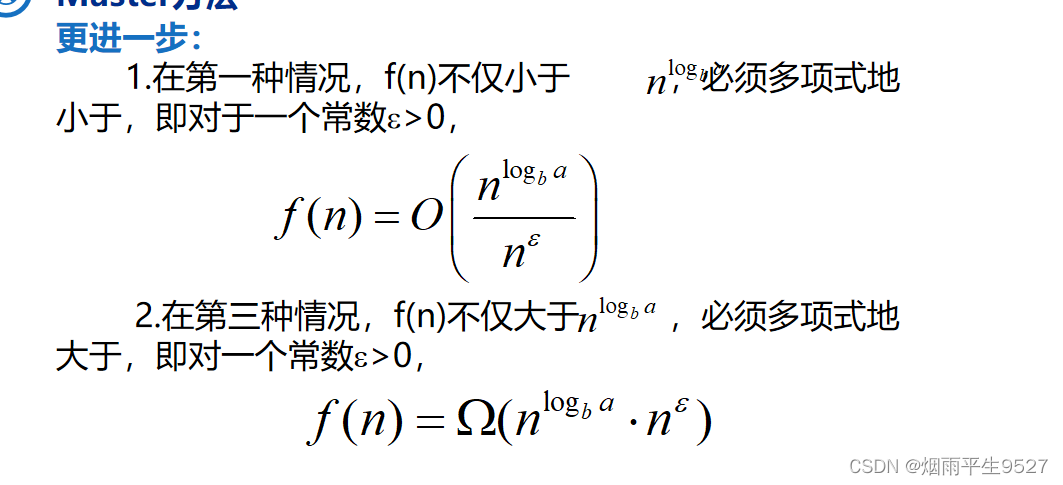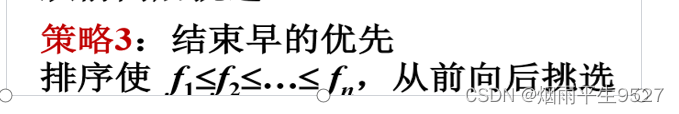前言:基本是为了我自己看的一些我容易忘记的东西,为考试作准备把
第一章
算法中的基本概念
程序设计=数据结构+算法
算法特性
1.有穷性
2.确定性
3.可行性
4.输出
5.输入
算法复杂性分析
算法复杂性依赖于:问题规模N,输入I,算法本身A
时间复杂性T和空间复杂性S
时间复杂度
1.Master定理
求解T(n)=aT(n/b)+f(n)型方程,
第二章
递归算法:直接或者间接调用自身的算法称为递归算法
分治法的基本步骤如下:
- 分解:将原问题分解为若干个规模较小的子问题,这些子问题相互独立且与原问题形式相同。
- 解决:递归地解决各个子问题。如果子问题的规模足够小,则直接解决。
- 合并:将各个子问题的解合并起来,构成原问题的解。
Strassen矩阵乘法:
- 问题描述:给定两个n*n的矩阵A B,求C=A*B;
改进:
第三章
动态规划通常用于解决具有重叠子问题和最优子结构的问题。
动态规划的基本步骤如下:
- 定义状态:定义一个状态数组,用于存储子问题的解。
- 状态转移方程:定义状态转移方程,用于描述如何从一个状态转移到另一个状态。
- 初始化:初始化状态数组中的某些值。
- 计算结果:根据状态转移方程和初始值,计算状态数组中的所有值,最终得到原问题的解。
备忘录方法 自顶向下的递归方式
动态规划算法 以自底向上
贪心算法以自顶向下的方式进行
第四章
贪心法是一种解决问题的方法,它在每一步都选择当前看起来最优的解,希望最终得到全局最优解。贪心法通常用于解决具有贪心选择性质和最优子结构的问题。
贪心法的基本步骤如下:
- 定义目标函数:定义一个目标函数,用于衡量解的优劣。
- 贪心选择:在每一步中,选择当前看起来最优的解。
- 证明正确性:证明贪心选择能够得到全局最优解。
贪心选择性 最优子结构
贪心法的适用范围
贪心策略适用的前提是:局部最优策略能导致产生全局最优解。
选择题填空题
程序设计=数据结构+算法
算法分析
大整数乘法:
问题描述:n位10进制整数X和Y,输出X和Y的乘积;
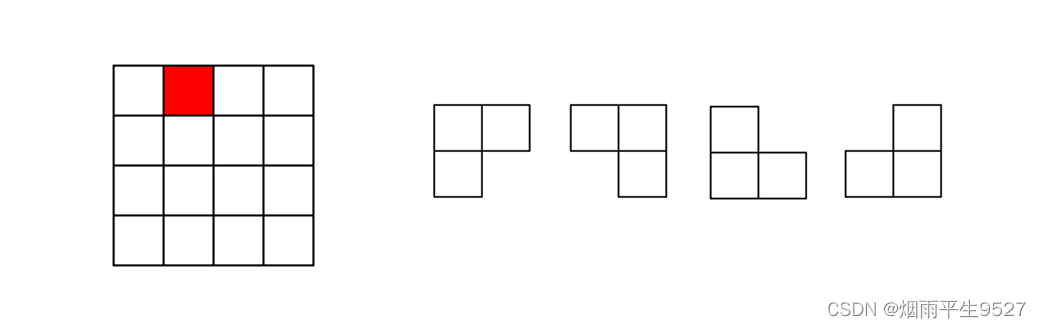
棋盘覆盖问题:
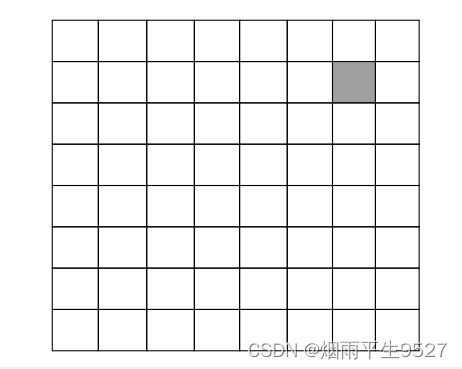
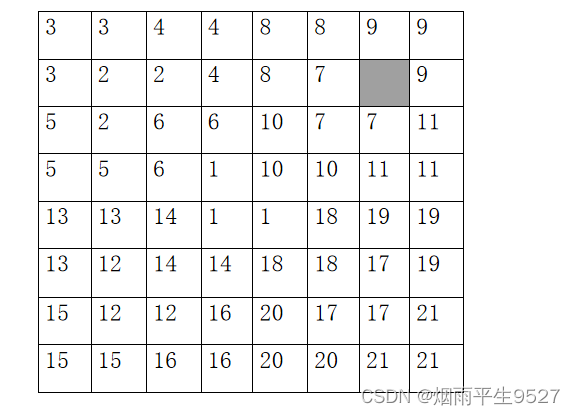
- 问题描述:在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在 棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格, 且任何2个L型骨牌不得重叠覆盖。
具体思想就是将一个大棋盘分割成4个小棋盘,有3个小棋盘中没有特殊方格,用一个L型的骨牌覆盖3个小棋盘的汇合处。按照左上、右上、左下、右下的方法递归覆盖。
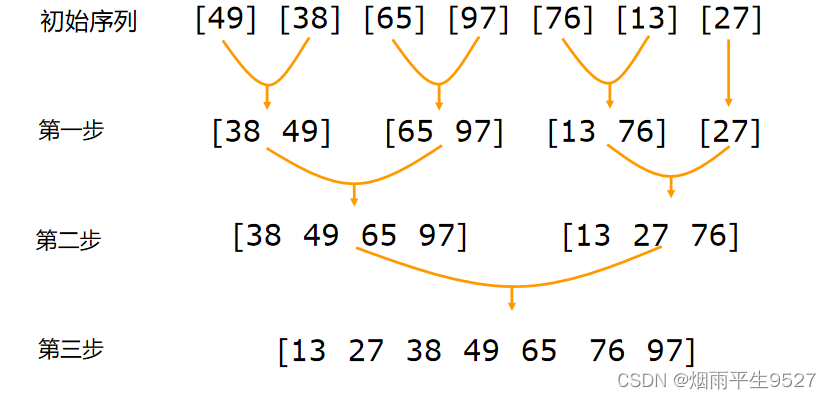
合并排序
改进
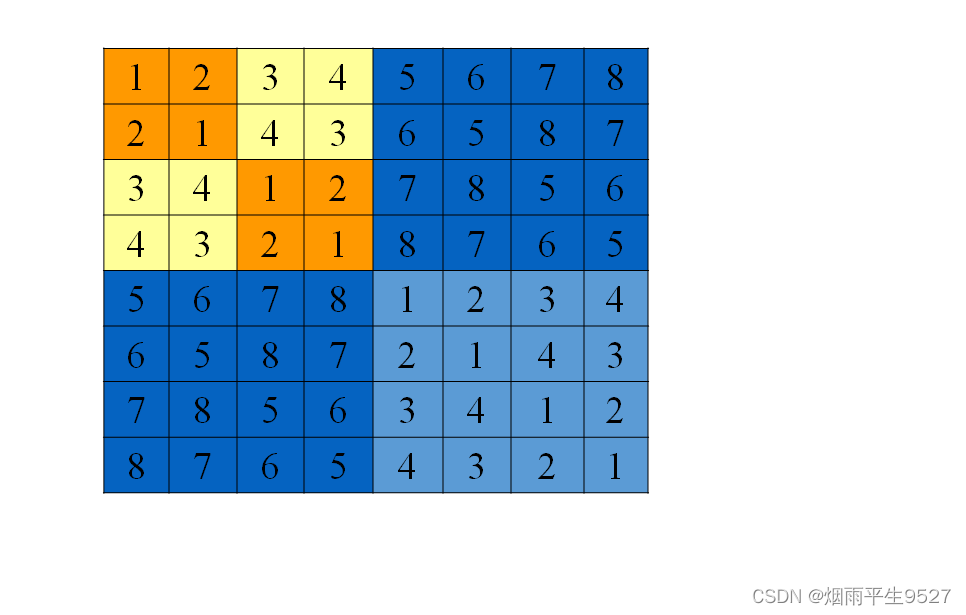
循环赛日程表:

矩阵连乘
最长公共子序列问题
思路
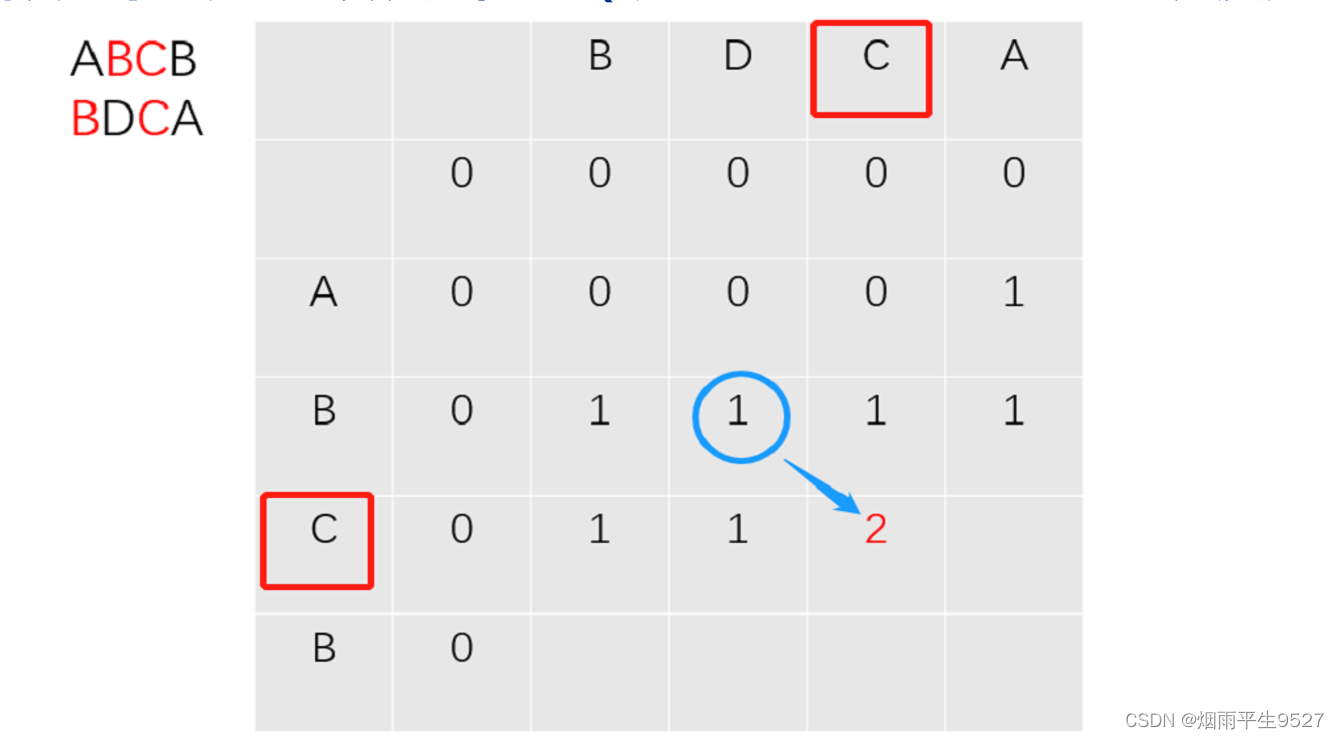
追踪
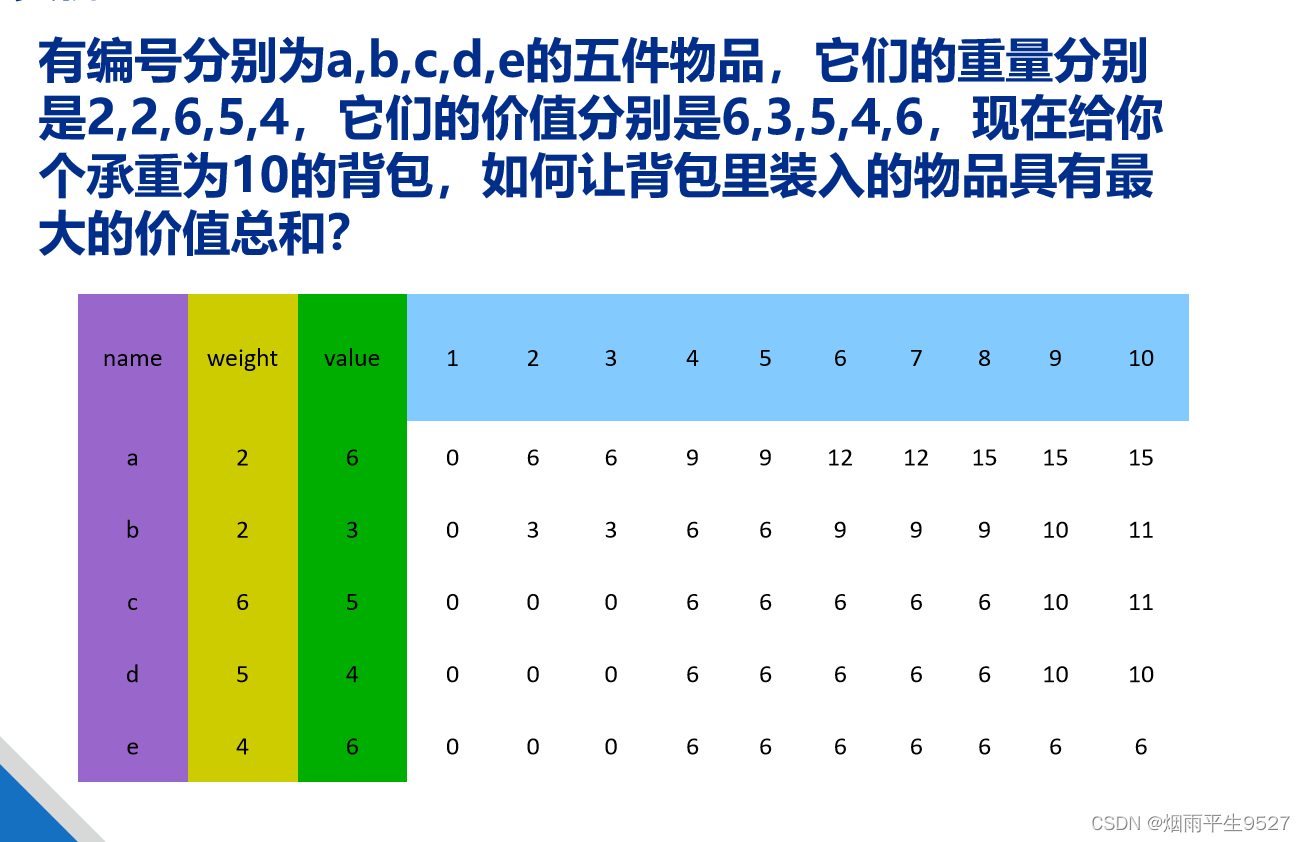
0-1背包
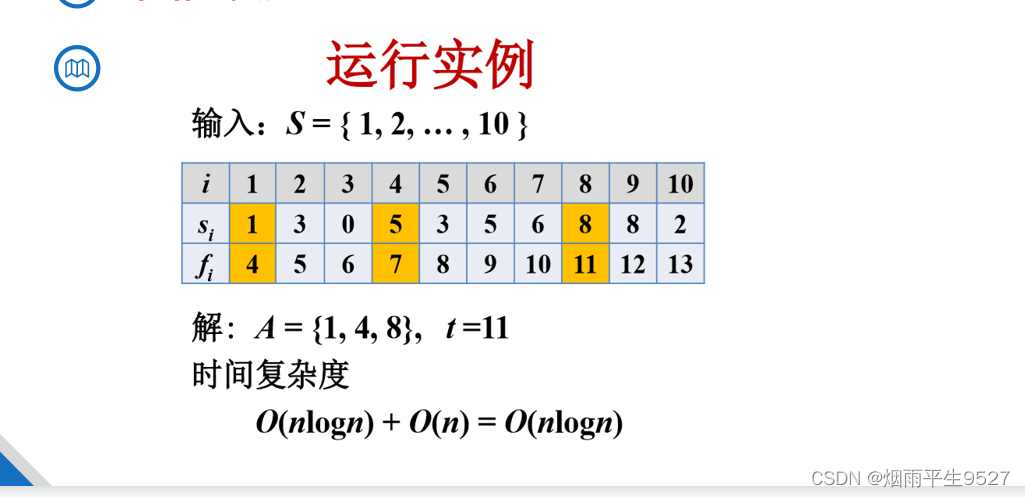
活动安排问题
程序设计
汉诺塔问题
问题描述:Hanoi问题起源于一个类似传说故事,在Hanoi这个地方有一个寺庙,这里有3根柱子和64个大小不同的金碟子。每个碟子有一个孔可以穿过。所有的碟子都放在第一个柱子上,而且按照从上到下碟子的大小依次增大的顺序摆设。如下图所示。现在,假定寺庙里的僧侣要移动这些碟子,将它们从柱子a移动到柱子b上。不过移动的规则如下: 1.每次只能从一个柱子的最上面移动一个碟子到另外一个柱子上。 2.不能将大碟子放到小碟子的上面。 按照前面这个规则,我们该怎么去移动这些碟子呢?
void hanoi(int n,char a,char b,char c)//将n个碟子从a移到b
{
if(n==0)
return;
else
{
hanoi(n-1,a,c,b);
move(a,b);
hanoi(n-1,c,b,a);
}
}
- 移动方法是从a->b->c->a,在移动圆盘的时候,若是奇数次移动,则将最小的圆盘移动到顺时针方向的下一个塔座上,若是偶数次移动,则在其他两个塔座之间,将较小的圆盘移动到另一个塔座上去;
全排序

void Perm(int list[], int k, int m)
{
if(k==m)
{ for(int i=0;i<=m;i++) cout<<list[i];
cout<<endl;
}
else
for(int i=k;i<=m;i++)
{
swap(list[k],list[i]);
Perm(list, k+1,m);
swap(list[k],list[i]);
} }快速排序
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=1e5+5;
int q[N];
void quick_sort(int *q,int l,int r)
{
if(l>=r)return;
int i=l-1,j=r+1,x=q[l+r+1>>1];
while(i<j)
{
do i++;while(q[i]<x);
do j--;while(q[j]>x);
if(i<j)swap(q[i],q[j]);
}
quick_sort(q,l,i - 1),quick_sort(q,i,r);
}
int main()
{
int n=0,x;
while(~scanf("%d",&x)&&x)q[++n]=x;
quick_sort(q,1,n);
for(int i=1;i<=n;i++)printf("%d ",q[i]);
}
合并排序
void MergeSort(Type a[], int left, int right)
{
if (left<right) {//至少有2个元素
int i=(left+right)/2; //取中点
MergeSort(a, left, i);
MergeSort(a, i+1, right);
Merge(a, b, left, i, right); //合并到数组b
copy(a, b, left, right); //复制回数组a
}
}
最大子段和问题

// 动态规划求解最大子段和问题
// n:数组a的元素个数
// a:待求最大子段和的数组
// c:保存子段和的起点
// d:返回最大子段和的终点
int MaxSum(int n, int *a, int *c, int *d) {
int *b, sum; // b数组保存以i结尾的最大子段和,sum保存当前找到的最大子段和
sum = 0;
b[0] = 0; // 初始化b[0]为0
for(i = 1; i <= n; i++) {
if(b[i-1] > 0) {
b[i] = b[i-1] + a[i]; // 如果前一个最大子段和是正数,则加上当前元素能获得更大的子段和
c[i] = 1; // 标记当前元素在前一个最大子段和中
} else {
b[i] = a[i]; // 如果前一个最大子段和是负数,则当前元素就是新的最大子段和的开头
c[i] = 0; // 标记当前元素为新的最大子段和的开头
}
if(b[i] > sum) { // 如果当前最大子段和比已知的最大子段和更大
sum = b[i]; // 更新最大子段和
(*d) = i; // 记录当前最大子段和的结束位置
}
}
return sum; // 返回最大子段和
}
0-1背包
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int v[MAXN]; // 体积
int w[MAXN]; // 价值
int f[MAXN][MAXN]; // f[i][j], j体积下前i个物品的最大价值
int main()
{
int n, m;
cin >> m >> n;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
{
// 当前背包容量装不进第i个物品,则价值等于前i-1个物品
if(j < v[i])
f[i][j] = f[i - 1][j];
// 能装,需进行决策是否选择第i个物品
else
f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
}
cout << f[n][m] << endl;
return 0;
}
最优装载
#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 10005;
int w[MAXN];
bool cmp(int a, int b) {
return a > b;
}
int main() {
int n, c;
cin >> n >> c;
for (int i = 1; i <= n; i++) {
cin >> w[i];
}
sort(w + 1, w + n + 1, cmp);
int sum = 0, cnt = 0;
for (int i = 1; i <= n; i++) {
if (sum + w[i] <= c) {
sum += w[i];
cnt++;
} else {
break;
}
}
cout << cnt << endl;
return 0;
}
活动安排
#include <bits/stdc++.h>
using namespace std;
const int N = 105;
int n,t;
int s[N],f[N];
void solve() {
if(f[1] > t)return;
cout <<"choose: 1 ";
int j = 1;
for(int i = 2; i <= n; ++i) {
if(s[i] >= f[j]) {
cout << i << " ";
j = i;
}
}
}
int main() {
cin >> n >> t;
for(int i = 1; i <=n ; ++i) {
cin >> s[i] >> f[i];
}
solve();
return 0;
}
/*输入
10 11
1 4
3 5
0 6
5 7
3 8
5 9
6 10
8 11
8 12
2 13
*/