背包问题基础与应用

背包问题

理论基础

01背包

背包中的每个物品只能用一次

物品编号	重量	价值
物品1	1	15
物品2	3	20
物品3	4	30

定义：dp[i][j]表示从下标0-i的物品中任取，放进容量为j的背包的最大价值

初始化：

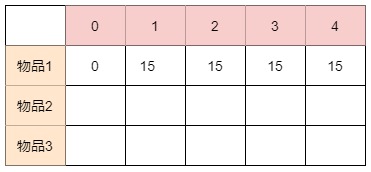
dp = [[0] * (bag_size + 1) for _ in range(len(weight))]
for j in range(1, bag_size + 1):
    if j >= weight[0]:
        dp[0][j] = value[0]

行为物品，列为背包容量。背包容量从0开始，所以列数为bag_size + 1

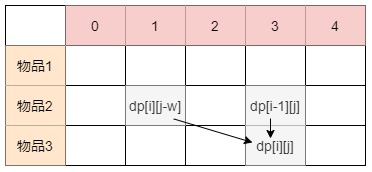
转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

将物品放入背包有两种选择：

不放当前物品，则延续前一物品的状态，用dp[i-1][j]表示
放入当前物品，则腾出空间，将当前物品放进去，维护dp数组，用dp[i-1][j-weight[i]] + value[i])表示

遍历顺序：

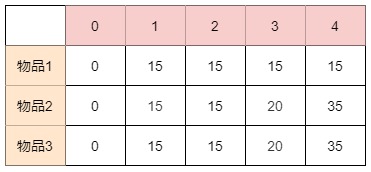
到底是先遍历物品呢？还是先遍历背包？

根据上图，dp[i][j]依赖于dp[i-1][j-w]和dp[i-1][j]，即左上角和正上方，画图可知两种遍历顺序都可以

1.先遍历物品，后遍历背包

    for i in range(1, len(weight)):  # 遍历物品
        for j in range(1, bag_size + 1):  # 遍历背包
            if j < weight[i]:
                dp[i][j] = dp[i-1][j]
            else:
                dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

2.先遍历背包，后遍历物品

    for j in range(1, bag_size + 1):
        for i in range(1, len(weight)):
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])

完整代码：

初始化的代码可以省略，类比在物品1之前，加了一个质量为0价值为0的物品0

def zero_one_bag(bag_size, weight, value):
    dp = [[0] * (bag_size + 1) for _ in range(len(weight))]
    for i in range(len(weight)):
        for j in range(1, bag_size + 1):
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
    return dp[-1][-1]


if __name__ == "__main__":
    bag_size = 4
    weight = [1, 3, 4]
    value = [15, 20, 30]
    zero_one_bag(bag_size, weight, value)

状态压缩：

仔细观察转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])

发现dp[i][j]的取值只依赖于上一行的值，而在for循环遍历过程中，上一行的数据已经计算过了，我们只需要把dp[i-1][j]和dp[i-1][j-w]的数据保留下来

具体做法：反向遍历背包，把dp[j]左边的数据当作备忘录，从右往左遍历的过程就是更新备忘录的过程

def zero_one_bag(bag_size, weight, value):
    dp = [0] * (bag_size + 1)
    for i in range(len(weight)):
        for j in range(bag_size, weight[i] - 1, -1):
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
    return dp[-1]

对比二维数组和一维数组发现少了两行代码：

if j < weight[i]:
    dp[i][j] = dp[i - 1][j]

因为一维数组从上往下滚动的过程中，如果在当前行不做更新，相当于沿用了上一行的数据，所以可以省略

完全背包

但凡刚才把滚动数组的遍历顺序写反了，完全背包的代码其实就写出来了

正向遍历滚动数组，就变成了完全背包（每个物品可以用无限次）：

反向遍历看到的是上一行，dp[i-1][j - weight[i]] + value[i]
正向遍历看到的是当前行，dp[i][j - weight[i]] + value[i]

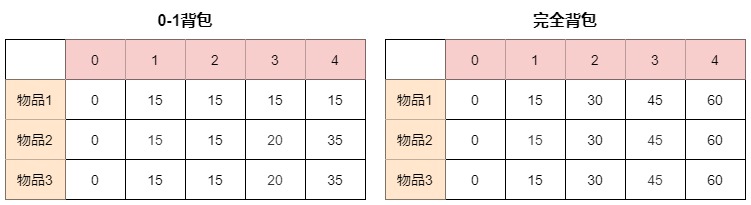
一维数组

def full_bag(bag_size, weight, value):
    dp = [0] * (bag_size + 1)
    for i in range(len(weight)):
        for j in range(weight[i], bag_size + 1):
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i])

二维数组

def full_bag(bag_size, weight, value):
    dp = [[0] * (bag_size + 1) for _ in range(len(weight))]
    for i in range(len(weight)):
        for j in range(1, bag_size + 1):
            if j < weight[i]:
                dp[i][j] = dp[i - 1][j]
            else:
                dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i])
    return dp[-1][-1]

应用举例

分割等和子集

416. 分割等和子集 - 力扣（Leetcode）

问题：给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

数组总和为total，判断数组能否用两个容量相等的背包装下

数组中的每个元素就是物品，重量和价值都为nums[i]
每个物品只能用一次
只需要判断一个背包的情况就行了

什么时候背包取得最大价值？答案是背包装满的时候，所以我们只需要判断背包的最大价值是否等于背包容量

class Solution:
    def canPartition(self, nums: List[int]) -> bool:
        total = sum(nums)
        if total % 2:
            return False
        target = total // 2
        dp = [0] * (target + 1)
        for i in range(len(nums)):
            for j in range(target, nums[i] - 1, -1):
                dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
        return dp[-1] == target

1049. 最后一块石头的重量 II - 力扣（Leetcode）

问题转换：将石头分成质量尽可能接近的两堆，求两堆的质量之差

数组中的元素是物品，质量和价值都是nums[i]
背包的容量为total//2，尽可能的装满背包，装的越满，质量差越小，刚好装满时质量差为0

class Solution:
    def lastStoneWeightII(self, stones: List[int]) -> int:
        total = sum(stones)
        target = total // 2
        dp = [0] * (target + 1)
        for stone in stones:
            for i in range(target, stone - 1, -1):
                dp[i] = max(dp[i], dp[i-stone] + stone)
        
        return total - 2 * dp[-1]

组合数

494. 目标和 - 力扣（Leetcode）

问题可以转换为：

数组nums中任取元素，一共有多少种和为target的组合
数组元素是物品，重量为nums[i]，目标和是背包容量，每个物品只能用一次，问把背包装满有多少种方法

class Solution:
    def findTargetSumWays(self, nums: List[int], target: int) -> int:
        total = sum(nums)
        if abs(target) > total or (total + target) % 2:
            return 0
        bag_size = (total + target) // 2
        dp = [0] * (bag_size + 1)
        dp[0] = 1
        for i in range(len(nums)):
            for j in range(bag_size, nums[i]-1, -1):
                dp[j] += dp[j-nums[i]]
        return dp[-1]

2400. 恰好移动 k 步到达某一位置的方法数目 - 力扣（Leetcode）

每一步都是1个单位，要么向右要么向左

问题：从数轴上点x移动到y，总共移动k步，有多少种方法？

假设向左一共移动a步，向右一共移动b步，则a + b = k, a - b = y - x，得到a = (k + y - x) // 2
问题转换为 $C_k^a$ ，求k个1中组合为a的方法数
物品的重量是1，求背包装满的方法数

class Solution:
    def numberOfWays(self, startPos: int, endPos: int, k: int) -> int:
        if ( k + endPos - startPos) % 2:
            return 0
        target = ( k + endPos - startPos) // 2
        dp = [0] * (target + 1)
        dp[0] = 1
        for _ in range(k):
            for j in range(target, 0, -1):
                dp[j] += dp[j-1]
        return dp[-1] % (10**9+7)

二维背包

474. 一和零 - 力扣（Leetcode）

问题转换：容量为m个0，n个1的背包，最多能装下多少物品。

背包的维度是二维，滚动数组的维度也是二维。每个物品只能用一次，依然是倒序遍历

dp[i][j]表示容量为i个0，j个1的背包的最大物品数
dp[i][j] = max(dp[i][j], dp[i-cnt0][j-cnt1] + 1)

class Solution:
    def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
        # dp[i][j]表示容量为i个0，j个1的背包的最大物品数
        dp = [[0] * (n + 1) for _ in range(m + 1)]
        for x in strs:
            cnt0 = x.count('0')
            cnt1 = len(x) - cnt0
            for i in range(m, cnt0 - 1, -1):
                for j in range(n, cnt1 - 1, -1):
                    dp[i][j] = max(dp[i][j], dp[i-cnt0][j-cnt1] + 1)
        return dp[m][n]

这一题如果不用滚动数组，dp数组应该是三维的

排列组合

518. 零钱兑换 II - 力扣（Leetcode）

硬币就是物品，金额就是背包容量

dp[i]表示装满背包的方法数，初始化dp[0]=1
dp[j] += dp[j-coins[i]]，每新来一个硬币，都要把当前硬币的贡献加上去

class Solution:
    def change(self, amount: int, coins: List[int]) -> int:
        # dp[i]表示凑出i的方法数
        dp = [0] * (amount + 1)
        dp[0] = 1
        for i in range(len(coins)):
            for j in range(coins[i], amount + 1):
                dp[j] += dp[j-coins[i]]
        return dp[-1]

377. 组合总和 Ⅳ - 力扣（Leetcode）

完全背包求排列数

滚动数组：先遍历背包，在遍历物品。因为背包容量每次更新，都要根据前面所有的物品去做选择

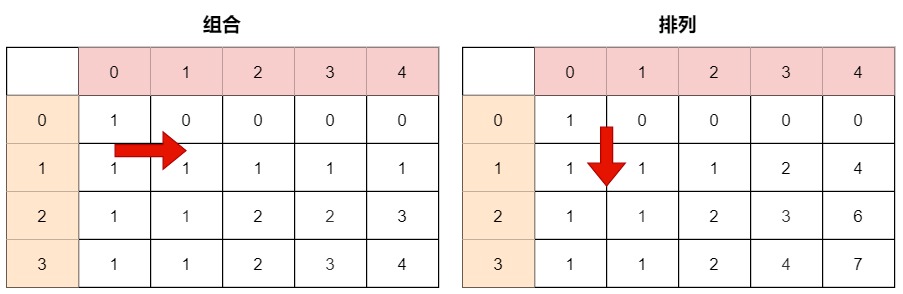
总结一下：

求组合数和排列数的内外层循环的遍历顺序相反，其他不变。
组合问题，看到的是当前物品和前面使用过的物品，限制是物品；排列问题，每次都能看到所有物品，限制是背包容量。

# 排列
class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [0] * (target + 1)
        dp[0] = 1
        for j in range(1, target + 1):
            for i in range(len(nums)):
                if nums[i] <= j:
                    dp[j] += dp[j-nums[i]]
        return dp[-1]
    
# 组合
class Solution:
    def combinationSum4(self, nums: List[int], target: int) -> int:
        dp = [0] * (target + 1)
        dp[0] = 1
        for x in nums:
            for i in range(x, target + 1):
                dp[i] += dp[i-x]
        return dp[-1]

扩展：

如果要穷举所有的排列数或者组合数呢，那就得用回溯算法了，暴力的尽头是递归。

穷举排列

class Solution:
    def __init__(self):
        self.path = []
        self.res = []

    def combinationSum4(self, nums: List[int], target: int) -> List[int]:

        def backTrace(cur):
            if cur == target:
                self.res.append(self.path[:])
                return

            for x in nums:
                if x + cur > target:
                    continue
                self.path.append(x)
                backTrace(cur + x)
                self.path.pop()

        backTrace(0)
        return self.res

穷举组合

那就需要去重了，每个for循环中，只用之前没有用过的数字

class Solution:
    def __init__(self):
        self.path = []
        self.res = []

    def combinationSum4(self, nums: List[int], target: int) -> List[int]:

        def backTrace(index, cur):
            if cur == target:
                self.res.append(self.path[:])
                return

            for i in range(index, len(nums)):
                if nums[i] + cur > target:
                    continue
                self.path.append(nums[i])
                backTrace(i, cur + nums[i])
                self.path.pop()

        backTrace(0, 0)
        return self.res

70. 爬楼梯 - 力扣（Leetcode）

爬楼梯其实也是排列问题，原题太简单了，把问题改成每次可以爬1~m个台阶，问有多少种爬楼梯的方式？

class Solution:
    def climbStairs(self, m: int, n: int) -> int:
        # 每次可以爬1~m个台阶
        dp = [0] * (n + 1)
        dp[0] = 1
        for i in range(1, n + 1):
            for j in range(1, m + 1):
                if j <= i:
                    dp[i] += dp[i-j]
        return dp[-1]

组合计数

279. 完全平方数 - 力扣（Leetcode）

完全背包，组合问题，先后遍历顺序都可以

class Solution:
    def numSquares(self, n: int) -> int:
        # dp[i] = min(dp[i-x**2], dp[i])
        dp = [n] * (n + 1)
        dp[0] = 0
        for i in range(1, n + 1):
            x = 1
            while x * x <= i:
                dp[i] = min(dp[i], dp[i-x*x] + 1)
                x += 1
        return dp[-1]

其他

139. 单词拆分 - 力扣（Leetcode）

单词是物品，句子是背包，每个单词可以用无限次，单词有顺序，所以是完全背包求排列，先遍历句子，再遍历单词

class Solution:
    def wordBreak(self, s: str, wordDict: List[str]) -> bool:
        n = len(s)
        dp = [False] * (n + 1)
        dp[0] = True
        for i in range(1, n + 1):
            r = i
            for w in wordDict:
                l = i - len(w)
                if l >= 0:
                    dp[r] = (dp[l] and s[l:r] == w) or dp[r]
        return dp[-1]