二：算法

        解决特定问题求解步骤的描述，在计算机中表现为指令的有限序列，并且每条指令表示一个或多个操作。

2.1 算法的特性

        算法具有五个基本特性：输入、输出、有穷性、确定性、可行性。

1）输入输出：

        算法具有零个或多个输入，至少有一个或多个输出。没有输出用这个算法就没有意义。

2）有穷性：

        算法在执行有限步骤后，自动结束而不会出现无限循环，并且每一个步骤在可接受的时间内完成。

3）确定性：

        算法的每一步骤都有确定的含义，不会出现二义性。

4）可行性：

        算法的每一步都必须是可行的，也就是说，每一步都能够通过执行有限次数完成。

        判断一个算法的效率时，函数中的常数和其他次要项常常可以忽略，而更应该关注主项（最高阶项）的阶数。

2.2  算法的时间复杂度

        在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法的时间量度，记作T(n)=O(f(n))。它表示随问题规模n的增大，算法执行睡觉哦考吗的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称为时间复杂度。其中f(n)是问题规模n的某个函数。

 

2.2.1  常见的时间复杂度

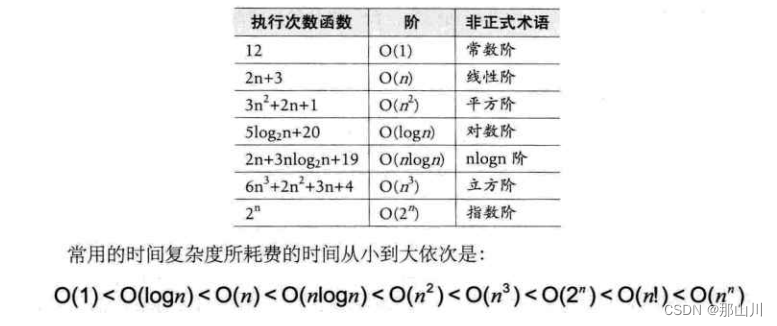
 2.3  算法的空间复杂度

        算法的空间复杂度通过计算算法所需的存储空间实现，算法空间复杂度的计算公式记作：S(n)=O(f(n)),其中，n为问题的规模，f(n)为语句关于n所占存储空间的函数。