考研数据结构--栈和队列

news2024/9/21 16:08:08

栈和队列

文章目录

  • 栈和队列
    • 栈
      • 栈的定义（特点）
      • 栈的存储表示
      • 栈的基本操作
      • 栈的顺序存储方式和基本操作实现
        • 顺序栈的定义
        • 顺序栈的初始化
        • 顺序栈的判空
        • 顺序栈的判满
        • 顺序栈的进栈
        • 顺序栈的出栈
        • 取栈顶元素
        • main函数测试
      • 栈的链式存储方式和基本操作实现
        • 链栈的定义
        • 链栈的初始化
        • 链栈的判空
        • 链栈的进栈
        • 链栈的出栈
        • 取栈顶元素
        • main函数测试
      • 栈的应用
        • 括号匹配(注意栈中数据元素类型改为char)
        • 表达式求值
          • 利用中缀转后缀的思想完成求值
        • 递归实现
          • 概述：
          • 优点：
          • 缺点：
          • 针对栈的缺点可以进行尾递归优化
    • 队列
      • 队列的链式存储
        • 定义
        • 初始化
        • 判空
        • 入队列
        • 出队列
        • 取队头元素
        • main 方法测试
      • 循环队列（顺序）
        • 定义
        • 初始化
        • 判空
        • 判满
        • 入队列
        • 出队列
        • 取对头元素
        • main方法测试

栈

内容

栈：栈的抽象数据类型定义、栈的存储表示及基本操作实现、栈的应用

栈的定义（特点）

栈是一种后进先出（LIFO）的线性表，只能在一端进行插入和删除操作，这一端称为栈顶，另一端称为栈底。

打个比方：

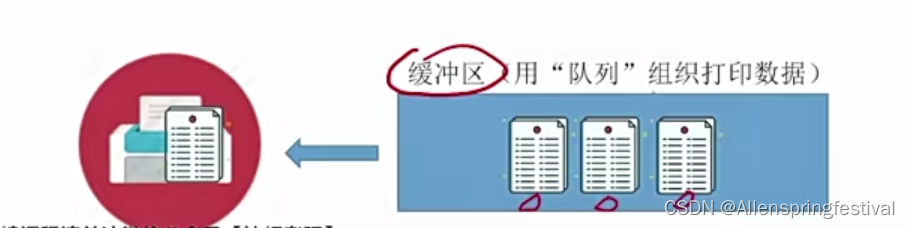
有一个胡同很窄只能通过一辆车，而且是死胡同，只能从胡同口进出，如果第一个进入，出去会很麻烦，需要所有的车辆出去后才能出去，如图：

在这里插入图片描述

栈的存储表示

栈的存储表示有两种方式：顺序栈和链栈。顺序栈是用一组地址连续的存储单元依次存放从栈底到栈顶的数据元素，用一个变量top记录栈顶元素的位置。链栈是用链表存放数据元素，每个结点包含数据域和指针域，用一个指针top指向栈顶结点。

顺序存储方式

在这里插入图片描述

链式存储方式

在这里插入图片描述

栈的基本操作

栈的基本操作有以下几种：

  • 初始化：创建一个空栈
  • 判空：判断栈是否为空
  • 进栈：在栈顶插入一个元素
  • 出栈：删除并返回栈顶元素
  • 取栈顶：返回但不删除栈顶元素

栈的顺序存储方式和基本操作实现

顺序栈的定义

//定义顺序栈结构体类型
#define MaxSize 50 //定义栈的最大长度
typedef struct{
    int data[MaxSize]; //存放栈中元素
    int top; //栈顶指针
}SqStack;

在这里插入图片描述

顺序栈的初始化

//初始化栈
void InitStack(SqStack &S){
    S.top = -1; //将栈顶指针置为-1，表示空栈
}

顺序栈的判空

//判断栈是否为空
bool Empty(SqStack S){
    return S.top == -1; //栈顶指针为-1，说明栈为空
}

顺序栈的判满

//判断栈是否已满
bool Full(SqStack S){
    return S.top == MaxSize - 1; //栈顶指针为MaxSize-1，说明栈已满
}

顺序栈的进栈

在这里插入图片描述

//进栈
bool Push(SqStack &S, int x){
    if(Full(S)) return false; //栈已满，无法进栈
    S.data[++S.top] = x; //栈顶指针加1，将元素x放入栈顶
    return true;
}

顺序栈的出栈

在这里插入图片描述

//出栈
bool Pop(SqStack &S, int &x){
    if(Empty(S)) return false; //栈为空，无法出栈
    x = S.data[S.top--]; //将栈顶元素赋值给x，栈顶指针减1
    return true;
}

取栈顶元素

//取栈顶元素
bool GetTop(SqStack S, int &x){
    if(Empty(S)) return false; //栈为空，无法取栈顶元素
    x = S.data[S.top]; //将栈顶元素赋值给x
    return true;
}

main函数测试

//测试代码
int main(){
    SqStack S;
    InitStack(S);
    if (Empty(S))printf("栈为空\n");
    if (Full(S)){
        printf("栈满\n");
    } else{
        printf("栈未满\n");
    };
    for(int i = 1; i <= 10; i++){
        Push(S, i);
    }
    int x;
    GetTop(S,x);
    printf("%d ", x);
    printf("\n");
    while(!Empty(S)){
        Pop(S, x);
        printf("%d ", x);
    }
    printf("\n");
    return 0;
}

栈的链式存储方式和基本操作实现

链栈的定义

//定义链栈结构体类型
typedef struct LinkNode{
    int data; //存放栈中元素
    struct LinkNode *next; //指向下一个结点的指针
}LinkNode, *LinkStack;

链栈的初始化

在这里插入图片描述

//初始化栈
void InitStack(LinkStack &S){
    S = NULL; //将栈顶指针置为NULL，表示空栈
}

链栈的判空

//判断栈是否为空
bool Empty(LinkStack S){
    return S == NULL; //栈顶指针为NULL，说明栈为空
}

链栈的进栈

在这里插入图片描述

//进栈
bool Push(LinkStack &S, int x){
    LinkNode *p = (LinkNode *)malloc(sizeof(LinkNode)); //分配新结点空间
    if(p == NULL) return false; //分配失败，返回false
    p->data = x; //将元素x赋值给新结点
    p->next = S; //新结点的指针域指向栈顶结点
    S = p; //栈顶指针指向新结点
    return true;
}

链栈的出栈

在这里插入图片描述

//出栈
bool Pop(LinkStack &S, int &x){
    if(Empty(S)) return false; //栈为空，无法出栈
    LinkNode *p = S; //p指向栈顶结点
    x = p->data; //将栈顶元素赋值给x
    S = p->next; //栈顶指针指向下一个结点
    free(p); //释放原栈顶结点空间
    return true;
}

取栈顶元素

//取栈顶元素
bool GetTop(LinkStack S, int &x){
    if(Empty(S)) return false; //栈为空，无法取栈顶元素
    x = S->data; //将栈顶元素赋值给x
    return true;
}

main函数测试

int main(){
    LinkStack S;
    InitStack(S);
    if (Empty(S))printf("栈为空\n");
    for(int i = 1; i <= 10; i++){
        Push(S, i);
    }
    int x;
    GetTop(S,x);
    printf("%d ", x);
    printf("\n");
    while(!Empty(S)){
        Pop(S, x);
        printf("%d ", x);
    }
    printf("\n");
    return 0;
}

栈的应用

栈的应用有很多，例如：

  • 括号匹配：用一个栈存放左括号，遇到右括号时出栈并匹配，最后判断栈是否为空

  • 表达式求值：用两个栈分别存放操作数和运算符，按照运算符优先级和结合性进行计算

  • 递归实现：用一个栈存放函数调用时的参数、返回地址和局部变量，实现递归过程

括号匹配(注意栈中数据元素类型改为char)

在这里插入图片描述

  1. switch语句匹配实现

    //栈的应用:括号匹配
bool BracketMatch(char exp[]){
    SqStack S; //定义一个顺序栈
    //LinkStack S;//定义一个链栈
    InitStack(S); //初始化栈
    for (int i = 0; exp[i] !='\0'; ++i) { //遍历表达式
        switch(exp[i]){ //根据字符类型进行分类讨论
            case '(':
            case '[':
            case '{':
                Push(S, exp[i]); //左括号进栈
                break;
            case ')':
            case ']':
            case '}':
                if(Empty(S)) return false; //栈为空，说明右括号多余
                char topElem;
                Pop(S, topElem); //取出栈顶元素
                if((exp[i] == ')' && topElem != '(') || //右括号与左括号不匹配
                   (exp[i] == ']' && topElem != '[') ||
                   (exp[i] == '}' && topElem != '{')){
                    return false;
                }
                break;
            default:
                break;
        }
    }
    return Empty(S); //如果栈为空，说明括号匹配
}

  2. if…else…判断语句实现

    //栈的应用:括号匹配
bool BracketMatch(char exp[]){
    SqStack S;
    InitStack(S);
    for(int i = 0; exp[i] != '\0'; i++){
        if(exp[i] == '(' || exp[i] == '[' || exp[i] == '{'){ //左括号进栈
            Push(S, exp[i]);
        }
        else if(exp[i] == ')' || exp[i] == ']' || exp[i] == '}'){ //右括号出栈
            if(Empty(S)) return false; //栈为空，说明右括号多余
            char topElem;
            Pop(S, topElem); //取出栈顶元素
            if(exp[i] == ')' && topElem != '(') return false; //右括号与左括号不匹配
            if(exp[i] == ']' && topElem != '[') return false; //右括号与左括号不匹配
            if(exp[i] == '}' && topElem != '{') return false; //右括号与左括号不匹配
        }
    }
    return Empty(S); //如果栈为空，说明括号匹配
}

main函数测试

int main(){
    char exp1[] = "((()))";
    char exp2[] = "(()())";
    char exp3[] = "(()))";
    char exp4[] = "((){}[])";
    char exp5[] = "((){[}])";
    if(BracketMatch(exp1)) printf("exp1匹配\n");
    else printf("exp1不匹配\n");
    if(BracketMatch(exp2)) printf("exp2匹配\n");
    else printf("exp2不匹配\n");
    if(BracketMatch(exp3)) printf("exp3匹配\n");
    else printf("exp3不匹配\n");
    if(BracketMatch(exp4)) printf("exp4匹配\n");
    else printf("exp4不匹配\n");
    if(BracketMatch(exp5)) printf("exp5匹配\n");
    else printf("exp5不匹配\n");
    return 0;
}

表达式求值

计算中缀表达式的值的代码是一种利用栈结构来实现的方法，它需要用到两个栈，一个用于存储操作数，一个用于存储运算符。它的基本思路是：

  1. 从左到右扫描中缀表达式，遇到操作数就压入操作数栈，遇到运算符就进行比较。
  2. 如果运算符栈为空，或者栈顶运算符为左括号，或者当前运算符优先级高于栈顶运算符，就直接压入运算符栈。
  3. 如果当前运算符为右括号，就依次弹出运算符栈顶的运算符，并从操作数栈中弹出相应的操作数，进行计算，并将结果压入操作数栈，直到遇到左括号为止，然后弹出左括号。
  4. 如果当前运算符优先级低于或等于栈顶运算符，就弹出栈顶运算符，并从操作数栈中弹出相应的操作数，进行计算，并将结果压入操作数栈，然后再次比较当前运算符和新的栈顶运算符，重复这个过程，直到满足条件2或者扫描完毕为止。
  5. 当中缀表达式扫描完毕后，如果运算符栈中还有运算符，就依次弹出，并从操作数栈中弹出相应的操作数，进行计算，并将结果压入操作数栈，直到运算符栈为空为止。
  6. 此时操作数栈中只有一个元素，就是最终的计算结果。

在这里插入图片描述

两个栈的代码

#include <cstdio>
#define MaxSize 50
//定义一个存储字符的栈结构
typedef struct {
    char data[MaxSize]; //用数组存储栈元素
    int top; //用一个变量记录栈顶位置
}SqStackChar;

//定义一个存储双精度浮点数的栈结构
typedef struct {
    double data[MaxSize]; //用数组存储栈元素
    int top; //用一个变量记录栈顶位置
}SqStackDouble;

//初始化字符栈，将栈顶位置设为-1，表示空栈
void InitStack(SqStackChar &S){
    S.top = -1;
}
//初始化双精度浮点数栈，将栈顶位置设为-1，表示空栈
void InitStack(SqStackDouble &S){
    S.top = -1;
}

//判断字符栈是否为空，如果为空返回true，否则返回false
bool Empty(SqStackChar S){
    return S.top ==-1;
}
//判断双精度浮点数栈是否为空，如果为空返回true，否则返回false
bool Empty(SqStackDouble S){
    return S.top ==-1;
}
//判断字符栈是否为满，如果为满返回true，否则返回false
bool Full(SqStackChar S){
    return S.top == MaxSize-1;
}
//判断双精度浮点数栈是否为满，如果为满返回true，否则返回false
bool Full(SqStackDouble S){
    return S.top == MaxSize-1;
}
//将一个字符压入字符栈，如果成功返回true，否则返回false
bool Push(SqStackChar &S,char n){
    if (Full(S))return false; //如果栈满，无法压入，返回false
    S.data[++S.top] = n; //将字符n存入栈顶位置，并将栈顶指针加一
    return true; //返回true表示成功
}
//将一个双精度浮点数压入双精度浮点数栈，如果成功返回true，否则返回false
bool Push(SqStackDouble &S,double n){
    if (Full(S))return false; //如果栈满，无法压入，返回false
    S.data[++S.top] = n; //将双精度浮点数n存入栈顶位置，并将栈顶指针加一
    return true; //返回true表示成功
}
//将一个字符从字符栈弹出，并赋值给n，如果成功返回true，否则返回false
bool Pop(SqStackChar &S,char &n){
    if (Empty(S))return false; //如果栈空，无法弹出，返回false
    n = S.data[S.top--]; //将栈顶元素赋值给n，并将栈顶指针减一
    return true; //返回true表示成功
}
//将一个双精度浮点数从双精度浮点数栈弹出，并赋值给n，如果成功返回true，否则返回false
bool Pop(SqStackDouble &S,double &n){
    if (Empty(S))return false; //如果栈空，无法弹出，返回false
    n = S.data[S.top--]; //将栈顶元素赋值给n，并将栈顶指针减一
    return true; //返回true表示成功
}

//取字符栈的栈顶元素，并赋值给n，如果成功返回true，否则返回false
bool GetTop(SqStackChar S,char &n){
    if (Empty(S))return false; //如果栈空，无法取得元素，返回false
    n = S.data[S.top]; //将栈顶元素赋值给n
    return true;//返回true表示成功
}
利用中缀转后缀的思想完成求值
//返回运算符的优先级
int Precedence(char op){
    switch(op){
        case '+': //加号的优先级为1
        case '-': return 1; //减号的优先级为1
        case '*': //乘号的优先级为2
        case '/': return 2; //除号的优先级为2
        case '(': return 0; //左括号的优先级为0，最低


    }
}

//对两个操作数进行运算
double Operate(double a, char op, double b){
    switch(op){
        case '+': return a + b; //加法运算
        case '-': return a - b; //减法运算
        case '*': return a * b; //乘法运算
        case '/': return a / b; //除法运算，注意除数不能为0
    }
}

//计算中缀表达式的值
double EvaluateExpression(char exp[]){
    SqStackChar notation; //定义一个存储运算符的栈
    SqStackDouble number; //定义一个存储运算数的栈
    InitStack(notation); //初始化运算符栈
    InitStack(number); //初始化运算数栈
    int i=0;
    while (exp[i] !='\0'){ //遍历中缀表达式的每个字符
        if(exp[i] >= '0' && exp[i] <= '9') { //如果是数字
            double x = 0;
            while (exp[i] >= '0' && exp[i] <= '9') { //将数字字符转换为数字
                x = x * 10 + exp[i] - '0';
                i++;
            }
            Push(number, x); //将数字压入操作数栈
        } else{ //如果是符号
            if (Empty(notation)) {
                Push(notation, exp[i]) ;//符号栈中无符号，直接入栈
                i++;
                continue;
            }
            if (exp[i] == '('){
                Push(notation, exp[i]) ;//符号为左括号，入栈
                i++;
                continue;
            }
            char op ;
            GetTop(notation,op); //获取符号栈顶的运算符
            if (exp[i] == ')') { //符号为右括号
                while (true) {
                    Pop(notation, op); //弹出符号栈顶的运算符
                    if (op != '(') { //如果不是左括号，说明还在括号内部，需要计算
                        double a = 0, b = 0;
                        Pop(number, b); //弹出操作数栈顶的两个数作为运算数
                        Pop(number, a);
                        Push(number, Operate(a, op, b)); //将运算结果压入操作数栈
                    } else { //如果是左括号，说明括号内部已经计算完毕，跳出循环
                        i++;
                        break;
                    }
                }
            } else if ( Precedence(exp[i]) > Precedence(op) ){ //如果当前符号的优先级大于符号栈顶的优先级，直接入栈
                Push(notation, exp[i]) ;
                i++;
                continue;
            } else{ //如果当前符号的优先级小于等于符号栈顶的优先级，需要先计算前面的表达式，再入栈
                Pop(notation,op); //弹出符号栈顶的运算符
                double a , b ;
                Pop(number,b); //弹出操作数栈顶的两个数作为运算数
                Pop(number,a);
                Push(number,Operate(a,op,b)); //将运算结果压入操作数栈
            }

        }
    }
    while (!Empty(notation)){ //当中缀表达式遍历完毕后，如果符号栈还有元素，继续计算直到为空
        char op;
        Pop(notation,op); //弹出符号栈顶的运算符
        double a , b ;
        Pop(number,b); //弹出操作数栈顶的两个数作为运算数
        Pop(number,a);
        Push(number,Operate(a,op,b)); //将运算结果压入操作数栈
    }
    double result;
    Pop(number, result); //弹出操作数栈的栈顶元素作为表达式的值
    return result;
}

main函数

int main(){
    char exp[MaxSize];
    //char exp[] = "20*(10+10)";
    printf("请输入中缀表达式：\n");
    scanf("%s", exp);
    printf("中缀表达式的值为：%lf", EvaluateExpression(exp));
    return 0;
}

递归实现

栈的应用：递归实现是一个常见的数据结构和算法的话题。递归是一种程序设计技巧，它可以让一个函数直接或间接地调用自身，从而将一个复杂的问题分解为更小的子问题。递归的实现需要借助栈这种数据结构，因为栈具有后进先出的特点，可以保存函数调用时的返回地址、参数、局部变量等信息，以便在函数返回时恢复现场。

概述：
  • 递归函数通常有三个部分：递归终止条件、递归前进段和递归返回段。当终止条件满足时，递归返回；当终止条件不满足时，递归前进；递归返回段是在每次递归调用之后执行的操作。
  • 递归函数在调用自身之前，会将当前的状态（包括参数、局部变量、返回地址等）压入栈中，形成一个调用帧；在调用自身之后，会从栈中弹出上一层的状态，恢复现场。所有的调用帧形成一个调用栈。
  • 递归函数可以看作是两个过程：“递"和"归”。"递"是指不断地向更小的子问题前进，直到达到终止条件；"归"是指从最小的子问题开始返回，依次执行返回段的操作，直到回到最初的问题。
优点：
  • 代码简洁清晰，可读性更好
  • 可以解决一些循环难以解决或无法解决的问题
  • 可以利用栈实现反向输出或倒序遍历
缺点：
  • 时间和空间消耗比较大，因为每次调用都需要分配栈空间和压入弹出数据
  • 很多计算都是重复的，因为同一个子问题可能会被多次调用
  • 调用栈可能会溢出，因为栈的大小是有限的
针对栈的缺点可以进行尾递归优化

尾递归是一种特殊的递归形式，它是指在函数的最后一步调用自身，而不需要做任何其他的操作。尾递归可以避免栈溢出的风险，也可以节省空间和时间，因为它不需要保存每次调用的状态，只需要保留一个栈帧即可。

//一个简单的递归函数，计算n的阶乘
int factorial(int n){
    if(n == 0 || n == 1){ //递归终止条件，当n为0或1时，返回1
        return 1;
    }
    else{ //递归调用，当n大于1时，返回n乘以n-1的阶乘
        return n * factorial(n-1);
    }
}

//一个简单的非递归函数，计算n的阶乘
int factorial(int n){
    int result = 1; //定义一个变量存储结果
    for(int i = 1; i <= n; i++){ //循环从1到n，依次乘以i
        result *= i;
    }
    return result; //返回结果
}

//一个尾递归函数，计算n的阶乘
int factorial(int n, int acc){ //定义一个累积参数acc，用来存储中间结果
    if(n == 0 || n == 1){ //递归终止条件，当n为0或1时，返回acc
        return acc;
    }
    else{ //递归调用，在最后一步将n-1和n乘以acc作为参数传入
        return factorial(n-1, n * acc);
    }
}

//调用尾递归函数时，需要将初始值1作为acc参数传入
int result = factorial(5, 1); //计算5的阶乘

队列

队列是一种先进先出（FIFO）的线性表，只允许在一端（称为队头）进行删除操作，而在另一端（称为队尾）进行插入操作。队列中没有元素时，称为空队列。

在这里插入图片描述

队列的存储表示有两种方式：顺序存储和链式存储。

队列的基本操作有以下几种：

  • 初始化操作：InitQueue(Q)。构造一个空队列Q。
  • 判空操作：QueueEmpty(Q)。判断队列Q是否为空，若为空则返回true，否则返回false。
  • 入队操作：EnQueue(Q)。将元素x插入到队列Q的队尾。
  • 出队操作：DeQueue(Q,x)。删除队列Q的队头元素，并用x返回其值。
  • 取队头操作：GetHead(Q,x)。用x返回队列Q的队头元素，但不删除该元素。

队列的链式存储

队列的链式存储是指使用链表来实现队列的存储结构。相比于顺序存储，链式存储不需要预先分配一定大小的空间，可以动态地分配和释放内存，因此更加灵活。同时，链式存储也避免了顺序存储中可能出现的“假溢出”问题。

在这里插入图片描述

方式1

定义

//
// Created by lenovo on 2023/4/17.
//
#include <cstdlib>
#include <cstdio>

// 链式队列结点
typedef struct LinkNode {
    int data; // 数据域
    LinkNode *next; // 指针域
}LinkNode;

// 链式队列结构体
typedef struct {
    LinkNode *front, *rear; // 队头指针和队尾指针
}LinkQueue;

初始化

// 初始化队列
void InitQueue(LinkQueue &Q){
    Q.front = Q.rear = (LinkNode*) malloc(sizeof(LinkNode)); // 初始化队头指针和队尾指针
    Q.front->next = NULL; // 队头指针的下一个结点为空
}

判空

// 判断队列是否为空
bool Empty(LinkQueue Q){
    return Q.front == Q.rear; // 队头指针等于队尾指针，说明队列为空
}

入队列

在这里插入图片描述

// 入队列
void EnQueue(LinkQueue &Q, int x){
    LinkNode *s = (LinkNode*) malloc(sizeof(LinkNode)); // 创建新结点
    s->data = x; // 将元素x放入新结点的数据域
    s->next = NULL; // 新结点的指针域为空
    Q.rear->next = s; // 将新结点插入队尾
    Q.rear = s; // 队尾指针指向新结点
}

出队列

在这里插入图片描述

// 出队列
bool DeQueue(LinkQueue &Q, int &x){
    if (Q.front == Q.rear) return false; // 队列为空，无法出队列
    LinkNode *s = Q.front->next; // 指向队头结点
    x = s->data; // 将队头元素赋值给x
    Q.front->next = s->next; // 队头指针指向下一个结点
    if (Q.rear == s) Q.rear = Q.front; // 如果队列为空，队尾指针置为NULL
    free(s); // 释放原队头结点空间
    return true;
}

取队头元素

// 取队头元素
bool GetHead(LinkQueue Q, int &x){
    if (Empty(Q)) return false; // 队列为空，无法取队头元素
    x = Q.front->next->data; // 将队头元素赋值给x
    return true;
}

main 方法测试

int main(){
    LinkQueue Q;
    InitQueue(Q); // 初始化队列
    if (Empty(Q)) printf("队列为空\n"); // 判断队列是否为空
    EnQueue(Q, 1); // 入队列
    EnQueue(Q, 2);
    EnQueue(Q, 3);
    EnQueue(Q, 4);
    EnQueue(Q, 5);
    int x;
    GetHead(Q, x); // 取队头元素
    printf("队头元素：%d\n", x);
    while (!Empty(Q)){ // 遍历队列
        DeQueue(Q, x); // 出队列
        printf("%d ", x);
    }
    printf("\n");
    if (Empty(Q)) printf("队列为空\n"); // 判断队列是否为空
    return 0;
}

方式2

//队列的抽象数据类型定义
typedef struct LinkNode{
    int data; //数据域
    struct LinkNode *next; //指针域
}LinkNode, *LinkQueue;

//队列的存储表示与基本操作实现
//初始化队列
void InitQueue(LinkQueue &Q){
    Q = (LinkNode*)malloc(sizeof(LinkNode)); //创建头结点
    Q->next = NULL; //头结点的指针域置为NULL
}

//判断队列是否为空
bool Empty(LinkQueue Q){
    return Q->next == NULL; //头结点的指针域为NULL，说明队列为空
}

//进队列
void CreateList_Tail(LinkQueue &L){
    int x;//输入的数据
    LinkNode *tailNode = L; //tailNode指向尾结点，初始时指向头结点
    scanf("%d",&x); //读入第一个数据
    while (x!=9999){ //用9999作为结束标志
        LinkNode *s = (LinkNode *) malloc(sizeof(LinkNode)); //分配新结点空间
        if (s == NULL) exit(-1); //分配失败退出
        s->next = NULL; //尾结点的指针域置空
        s->data = x; //新结点的数据域赋值为x
        tailNode->next = s; //原尾结点的指针域指向新结点
        tailNode = s; //tailNode指向新的尾结点
        scanf("%d",&x); //读入下一个数据
    }
    // tailNode->next =NULL
}

//出队列
bool DeQueue(LinkQueue &Q, int &x){
    if(Empty(Q)) return false; //队列为空，无法出队列
    LinkNode *p = Q->next; //p指向队头结点
    x = p->data; //将队头元素赋值给x
    Q->next = p->next; //队头指针指向下一个结点
    if(Q->next == NULL) Q = NULL; //如果队列为空，队尾指针置为NULL
    free(p); //释放原队头结点空间
    return true;
}

//取队头元素
bool GetHead(LinkQueue Q, int &x){
    if(Empty(Q)) return false; //队列为空，无法取队头元素
    x = Q->next->data; //将队头元素赋值给x
    return true;
}

int main(){
    LinkQueue Q;
    InitQueue(Q);
    if (Empty(Q))printf("队列为空\n");
    CreateList_Tail(Q);
    int x;
    GetHead(Q,x);
    printf("对头元素：%d\n",x);
    while(!Empty(Q)){
        DeQueue(Q, x);
        printf("%d ", x);
    }
    printf("\n");
    return 0;

}

循环队列（顺序）

循环队列是一种线性数据结构，它具有队列的所有特点，同时在实现上采用了循环数组的思想，可以更高效地利用存储空间。

在循环队列的实现中，需要维护队头指针和队尾指针，它们的初始值都为0，表示空队列。

当队列中有元素进队列时，队尾指针加1；当队列中有元素出队列时，队头指针加1。

为了实现循环，当队尾指针到达数组的末尾时，需要将其置为0，从而形成一个循环。

定义

//
// Created by lenovo on 2023/4/17.
//
#include <cstdlib>
#include <cstdio>

#define MAXSIZE 5

//队列的抽象数据类型定义
typedef struct{
    int data[MAXSIZE]; //存放队列元素
    int front, rear; //队头指针和队尾指针
}SqQueue;

初始化

//队列的存储表示与基本操作实现
//初始化队列
void InitQueue(SqQueue &Q){
    Q.front = Q.rear = 0; //队头指针和队尾指针置为0，表示空队列
}

判空

//判断队列是否为空
bool Empty(SqQueue Q){
    return Q.front == Q.rear; //队头指针等于队尾指针，说明队列为空
}

判满

//判断队列是否已满
bool Full(SqQueue Q){
    return (Q.rear + 1) % MAXSIZE == Q.front; //队尾指针的下一个位置等于队头指针，说明队列已满
}

入队列

//进队列
bool EnQueue(SqQueue &Q, int x){
    if(Full(Q)) return false; //队列已满，无法进队列
    Q.data[Q.rear] = x; //将元素x放入队尾
    Q.rear = (Q.rear + 1) % MAXSIZE; //队尾指针加1
    return true;
}

出队列

//出队列
bool DeQueue(SqQueue &Q, int &x){
    if(Empty(Q)) return false; //队列为空，无法出队列
    x = Q.data[Q.front]; //将队头元素赋值给x
    Q.front = (Q.front + 1) % MAXSIZE; //队头指针加1
    return true;
}

取对头元素

//取队头元素
bool GetHead(SqQueue Q, int &x){
    if(Empty(Q)) return false; //队列为空，无法取队头元素
    x = Q.data[Q.front]; //将队头元素赋值给x
    return true;
}

main方法测试

int main(){
    SqQueue Q;
    InitQueue(Q);
    if (Empty(Q))printf("队列为空\n");
    EnQueue(Q,1);
    EnQueue(Q,2);
    EnQueue(Q,3);
    EnQueue(Q,4);
    EnQueue(Q,5);
    if (Full(Q))printf("队列为满\n");
    int x;
    GetHead(Q,x);
    printf("对头元素：%d\n",x);
    while(!Empty(Q)){
        DeQueue(Q, x);
        printf("%d ", x);
    }
    printf("\n");
    return 0;

}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/431602.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

sentiel安装与整合

sentiel安装与整合

（1）方案一：超时处理 设定超时时间，请求超过一定时间没有响应就返回错误信息，不会无休止等待（只能缓解，不能从根本上解决） （2）方案二：舱壁模式 限定每个业务能使用的线程数，避免耗尽整个tomcat的资源，因此也叫线程隔离。（会造成资源浪费） （3）方案三：熔断降…
阅读更多...
不坑盒子 + 智能写作（Office、WPS插件）助你高效办公，早点下班回家。

不坑盒子 + 智能写作（Office、WPS插件）助你高效办公，早点下班回家。

不坑盒子简介 很多朋友在工作过程中需要对Word文档进行编辑处理&#xff0c;如果想让Word排版更有效率可以试试小编带来的这款不坑盒子软件&#xff0c;这是一个非常好用的插件工具&#xff0c;专门应用在Word文档中&#xff0c;支持Office 2010以上的版本&#xff0c;用户可以…
阅读更多...
ntp时间服务器配置，ssh免密登录 rhce（22）

ntp时间服务器配置，ssh免密登录 rhce（22）

目录 1.配置ntp时间服务器&#xff0c;确保客户端主机能和服务端主机同步时间. 2.配置ssh免密登录&#xff0c;能够通过客户端主机通过redhat用户和服务端主机基于公钥验证方式进行远程连接 1.配置ntp时间服务器&#xff0c;确保客户端主机能和服务端主机同步时间. 安装时间…
阅读更多...
(链表专题) 234. 回文链表——【Leetcode每日一题】

(链表专题) 234. 回文链表——【Leetcode每日一题】

234. 回文链表 给你一个单链表的头节点 head &#xff0c;请你判断该链表是否为回文链表。如果是&#xff0c;返回 true &#xff1b;否则&#xff0c;返回 false 。 示例 1&#xff1a; 输入&#xff1a;head [1,2,2,1] 输出&#xff1a;true 示例 2&#xff1a; 输入&…
阅读更多...
【蓝桥杯】数组中存在K倍区间的子数组个数

【蓝桥杯】数组中存在K倍区间的子数组个数

文章目录 前言题目分析算法难度实战1、创建算法2、创建测试用例3、运行测试用例4、测试结果 总结 前言 蓝桥杯全国软件和信息技术专业人才大赛由工业和信息化部人才交流中心主办,每年参赛人数超过30000人。蓝桥杯大赛作为国内领先的全国性 IT 学习赛事&#xff0c;持续有力支撑…
阅读更多...
Python爬虫自动化从入门到精通第9天(爬虫数据的存储)

Python爬虫自动化从入门到精通第9天(爬虫数据的存储)

爬虫数据的存储 数据存储概述MongDB数据库的概念MongDB的安装使用PyMongo库存储到数据库 数据存储概述 通常&#xff0c;从网页爬取到的数据需要进行分析、处理或格式化&#xff0c;然后进行持久化存储&#xff0c;以备后续使用。数据存储主要有以下两种方式&#xff1a; 1&am…
阅读更多...
启动kafka报错ERROR Fatal error during KafkaServer startup. Prepare to shutdown

启动kafka报错ERROR Fatal error during KafkaServer startup. Prepare to shutdown

一、错误 报的错&#xff1a; ERROR Fatal error during KafkaServer startup. Prepare to shutdown (kafka.server.KafkaServer) kafka.common.InconsistentBrokerIdException: Configured broker.id 0 doesn’t match stored broker.id Some(1) in meta.properties. If you m…
阅读更多...
跟ChatGPT聊天、需求润色优化，禅道OpenAI 插件发布

跟ChatGPT聊天、需求润色优化，禅道OpenAI 插件发布

禅道插件上新了&#xff0c;OpenAI 禅道集成&#xff0c;可提供神奇海螺聊天、需求润色功能。 神奇海螺 “章鱼哥&#xff0c;你为什么不问问神奇海螺呢&#xff1f;”——海绵宝宝 那么&#xff0c;就让我们问一问神奇 海螺吧&#xff01;禅道上线神奇海螺功能&#xff0c;…
阅读更多...
【C++】优先级队列，反向迭代器

【C++】优先级队列，反向迭代器

文章目录 priority_queue的介绍和使用priority_queue的使用 反向迭代器 priority_queue的介绍和使用 优先队列是一种容器适配器&#xff0c;根据严格的弱排序标准&#xff0c;它的第一个元素总是它所包含的元素中最大的。此上下文类似于堆&#xff0c;在堆中可以随时插入元素&a…
阅读更多...
数据分析之Pandas 基础入门

数据分析之Pandas 基础入门

一、初始Pandas pandas 是数据分析三大件之一&#xff0c;是Python的核心分析库&#xff0c;它提供了快捷、灵活、明确的数据结构&#xff0c;它能够简单、直观、快速的处理各种类型的数据结构。 pandas 支持的数据结构如下&#xff1a; SQL 或Excel 类似的数据有序或无序的…
阅读更多...
后端程序员必须学会的编辑器vim

后端程序员必须学会的编辑器vim

vim编辑器使用小结 1. vim简介 Vim是一个类似于Vi的著名的功能强大、高度可定制的文本编辑器&#xff0c;在Vi的基础上改进和增加了很多特性。VIM是自由软件。Vim普遍被推崇为类Vi编辑器中最好的一个&#xff0c;事实上真正的劲敌来自Emacs的不同变体。1999 年Emacs被选为Lin…
阅读更多...
MyBatis(十一)、MyBatis查询语句专题

MyBatis(十一)、MyBatis查询语句专题

准备工作&#xff1a; 模块名&#xff1a;mybatis-007-select 打包方式&#xff1a;jar 引入依赖&#xff1a;mysql驱动依赖、mybatis依赖、logback依赖、junit依赖。 引入配置文件&#xff1a;jdbc.properties、mybatis-config.xml、logback.xml 创建pojo类&#xff1a;Car 创…
阅读更多...
SQL sever数据库----基础增删改查操作与where条件限制

SQL sever数据库----基础增删改查操作与where条件限制

where条件限制方法 在SQL sever中使用where语句&#xff0c;可以对各种操作添加限制条件 基础格式为 ———————— where 逻辑表达式 例如限制条件的查询 select 范围 from 表名 where 逻辑表达式 逻辑表达式就是一个判断 如 a > 5 、a6>9、a>5 and b>5 各种…
阅读更多...
k8s部署流水账

k8s部署流水账

久仰大名k8s&#xff0c;业余选手一直望而却步。最近终于初步炮制成功。知道了大概的流程。本篇为部署备忘录。 经过的大环节有&#xff1a;修改树莓派/boot/cmdline.txt甚至/cmd/config.txt里面的集群相关设置&#xff0c;把cgroup驱动enable好。swap关掉。这些都是所有集群内…
阅读更多...
比较几种热门Hybrid App前端框架

比较几种热门Hybrid App前端框架

作为一种既能够在原生应用程序环境中运行&#xff0c;也能够在 Web 浏览器中运行的应用程序&#xff0c;Hybrid App 主要使用 Web 技术进行开发&#xff0c;如 HTML、CSS 和JavaScript&#xff0c;并使用一个中间层将其封装在原生应用程序中。随着技术的持续推进&#xff0c;Hy…
阅读更多...
3.3栈和队列的应用

3.3栈和队列的应用

3.3.1括号匹配问题 IDE可视化的编程环境 作为一名程序开发人员&#xff0c;不管你使用哪门语言开发都有很多可以选择的集成开发环境IDE&#xff08;Integrated Development Environment&#xff09;&#xff0c;IDE是提供程序开发环境的应用程序&#xff0c;一般包括代码编辑器…
阅读更多...
程序员挣够了钱，到中年失业真的很可怕吗？

程序员挣够了钱，到中年失业真的很可怕吗？

借用最近很火的一张图&#xff0c;看看没有工作&#xff0c;你手里的存款够用几年&#xff08;按每年年化3.5%&#xff0c;利息继续放入理财计算&#xff09;&#xff1a; 如果每年花销在10万左右&#xff08;折合每个月8333元&#xff0c;应该是比较富足的&#xff09;&#x…
阅读更多...
字节跳动高频 “ 120道 ” 软件测试面试题解析

字节跳动高频 “ 120道 ” 软件测试面试题解析

1、web测试和APP测试的区别&#xff1f; web测试和APP测试都离不开测试的基础知识和测试原理。 不同点是&#xff1a;web 测试更多的是考虑自身功能和浏览器兼容&#xff0c;app 测试要考虑手机本身固有的属性&#xff0c;所以 app 测试还需要注意以下几点&#xff1a; 中断…
阅读更多...
FreeRTOS 事件组

FreeRTOS 事件组

实现功能&#xff0c;当任务A,B完成后执行串口任务。 不同任务用不同的位表示 configUSE_16_BIT_TICKS1,bitx(0~7)&#xff1b; configUSE_16_BIT_TICKS设置为0 &#xff0c;bitx(0~23)&#xff1b; //串口任务的头文件 #ifndef __TRANSMIT_H #define __TRANSMIT_H#include…
阅读更多...
nVisual创建机柜流程

nVisual创建机柜流程

一、制作机柜 1.先在绘图软件中把机柜画出来 2.把机柜导出一张SVG格式的图片 二、创建机柜 1.打开nVisual右上角点击管理选择模型库 2.选择设备点击新增&#xff0c; 依次录入机柜品牌、型号、宽高深等基础数据&#xff0c; 再上传相应的前视图&#xff08;在系统里展示…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023