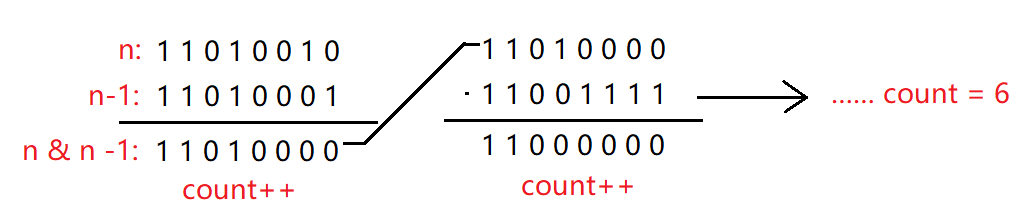哈希的应用——bitset(STL)位图

一、bitset的介绍

1.位图的引入

看这样一道面试题：

给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

单纯从判断一个数是否在一串数字的角度看，我们很容易想到下面的方法：

1. 把这40亿个整数放到set、unordered_set容器里头，调用find函数来判断
2. 把这40亿个整数进行外排序，再去二分查找

单就此题而言，为了推翻上面两种方法，首先，我们要清楚40亿个整数，占用多少空间：

• 计算得知，40亿整数占16个G内存，光数据就占了16G，若放到set容器，其底层红黑树的内部也有负载的消耗（存颜色，三叉连……），再算上16G的消耗，消耗太大了，内存不够，承受不住。同理，内存不够，数据压根放不到内存，也就不能进行排序。

为了解决此问题，这就需要我们用到位图来解决。

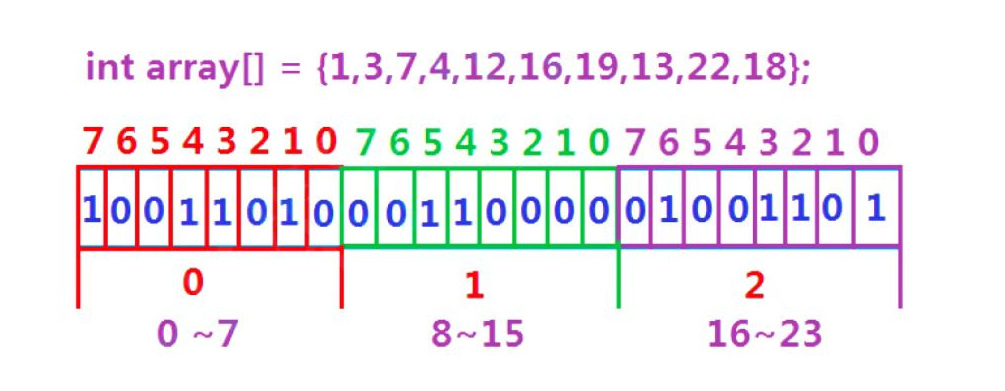
• **我们在判断一个数据是否在给定的整形数据中，结果只有在或者不在这两种状态，那么就可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在。这里我们采用直接定址法的哈希，用一个比特位标识映射值在不在，这就是位图。**示例：

对于40亿个整数，我们要我们要开整型的最大值（2^32 - 1）个bit位，大概占500MB的内存：

由此可见，使用位图的方法，大大减少了内存的消耗，并且能很好的解决此问题。

---

2.位图的概念

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用来判断某个数据存不存在的。

---

3.位图的应用

1. 快速查找某个数据是否在一个集合中
2. 排序 + 去重
3. 求两个集合的交集、并集等
4. 操作系统中磁盘块标记

---

二、bitset的使用

1.bitset的构造方式

1、使用默认构造函数，构造一个16位的位图，默认初始化为0

bitset<16> bs1;

2、元素按照给定整数的二进制位进行初始化：0xff ——> 1111 1111

bitset<16> bs2(0xfa2);//0000111110100010

3、使用01的string进行初始化：std::string(“01101001”) ——> 01101001

bitset<16> bs3(string("01101001"));//0000000001101001

4、使用01的字符串进行初始化：(“01101001”) ——> 01101001

bitset<16> bs4("01101001");//0000000001101001

---

2.bitset成员函数的使用

bitset常用成员函数如下表格所示：

成员函数	功能
set	设置指定位或所有位
reset	清空指定位或所有位
flip	反转指定位或所有位
test	获取指定位的状态
count	获取被设置位的个数
size	获取可以容纳的位的个数
any	如果有任何一个位被设置则返回true
none	如果没有位被设置则返回true
all	如果所有位都被设置则返回true

示例：

int main()
{
	bitset<16> bs;
	bs.set(4);
	bs.set(6);
	bs.set(2);
	cout << bs.size() << endl;//16
	cout << bs << endl;//0000000001010100
	//获取指定位的状态
	cout << bs.test(0) << endl;//0
	cout << bs.test(2) << endl;//1
	//反转所有位
	bs.flip();
	cout << bs << endl;//1111111110101011
	//反转第1位
	bs.flip(1);
	cout << bs << endl;//1111111110101001
	cout << bs.count() << endl;//12
	//清空第3位
	bs.reset(3);
	cout << bs << endl;//1111111110100001
	//清空所有位
	bs.reset();
	cout << bs.none() << endl;//1
	cout << bs.any() << endl;//0
	//设置所有位
	bs.set();
	cout << bs.all() << endl;//1
	return 0;
}

注意： 使用成员函数set、reset、flip时，若指定了某一位则操作该位，若未指定位则操作所有位。

---

3.bitset运算符的使用

如表格所示：

运算符	功能说明
>>、<<	输入输出运算符
=	赋值运算符
==、!=	关系运算符
&=、|=、^=、<<=、>>=	复合赋值运算符
~	单目运算符
&、|、^	位运算符
[ ]	operator[ ]运算符

示例：

int main()
{
	//>>输入、<<输出运算符
	bitset<8> bs;
	cin >> bs;//10100
	cout << bs << endl;//00010100
	//复合赋值运算符
	bitset<8> bs1("101011");
	bitset<8> bs2("100100");
	cout << (bs1 >>= 2) << endl;//00001010
	cout << (bs2 |= bs1) << endl;//00101110
	//位运算符
	bitset<8> bs3("10010");
	bitset<8> bs4("11001");
	cout << (bs3 & bs4) << endl;//00010000
	cout << (bs3 ^ bs4) << endl;//00001011
	//operator[]运算符
	cout << bs3[4] << endl;//1
	cout << bs3[2] << endl;//0
}

---

三、bitset位图的模拟实现

1.位图的基本框架

• bitset能实现对数字的位的操作，同时也能通过类似于数组的下标来访问各个位的数值，以执行相应的操作。模拟bitset就是用一个普通的数组来存储数据以达到模拟的目的。
• 如果我们以一个整型作为比特位的容器，那么如果要求0~N范围的比特位，就需要有N/32+1 个整型来容纳这些比特位，同理如果以char为容器，则需要N/8+1个char来容纳N个比特位。这里我们用vector数组作为底层容纳比特位的容器，且其存储的数据类型为char。

namespace bitset_realize
{
	//N个比特位的位图
	template<size_t N>
	class bitset
	{
	public:
		//构造函数
		bitset();
		//把x映射的位标记成1
		void set(size_t x);
		//把x映射的位标记成0
		void reset(size_t x);
		//判断指定比特位x的状态是否为1
		bool test(size_t x);
		//翻转指定pos
		void flip(size_t x);
		//获取位图中可以容纳位N的个数
		size_t size()
		//统计set中1的位数
		size_t count();
		//判断所有比特位若无置为1，返回true
		bool none();
		//判断位图中是否有位被置为1，若有则返回true
		bool any();
		//全部NUM个bit位被set返回true
		bool all();
	private:
		vector<char> _bits;//位图
	};
}

---

2.成员函数

2.1.构造函数

• 一个char类型有8个bit位，所以理想状态下N个比特位的位图就需要用到N / 8个字节，但仅限于N是8的整数倍，如果N位10，那么计算下来就会少2个比特位，因此综合考虑，我们给出N / 8 + 1个字节，这样算下来，所需的N个比特位绝对都能访问到，最多可以整除的情况下浪费了8个比特位（1字节）

而构造函数，我们只需要对这所有的比特位（N / 8 + 1）个字节的大小初始化为0即可。

//构造函数
bitset()
{
	//+1保证足够比特位，最多浪费8个比特位
	_bits.resize(N / 8 + 1, 0);
}

---

2.2.set reset test

• 1、set

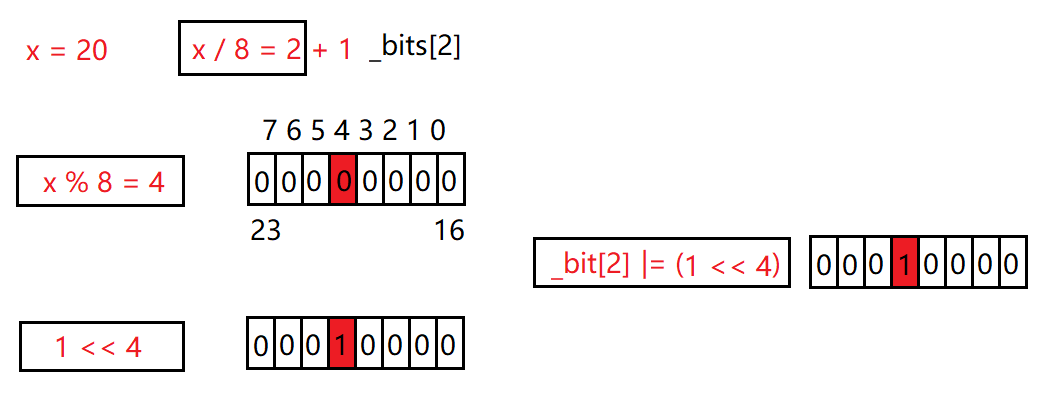
set的作用是把x映射的位置标记成1，实现规则如下：

1. 通过x / 8计算x在第i个char类型
2. 通过x % 8计算x在char第j个比特位
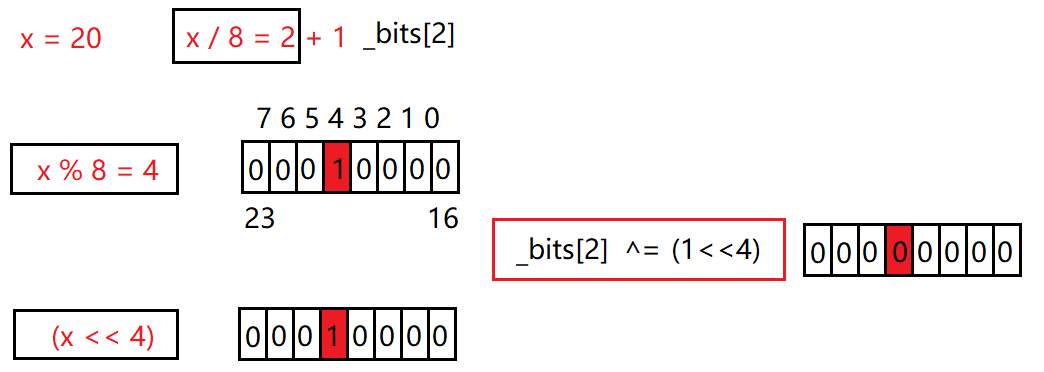
3. 利用按位或 | 把第i个char中的第j个比特位置为1

//把x映射的位标记成1
void set(size_t x)
{
	//x映射的比特位在第几个char对象
	size_t i = x / 8;
	//x在char第几个比特位
	size_t j = x % 8;
	//利用按位或|把第j位标记成1
	_bits[i] |= (1 << j);
}

• 2、reset

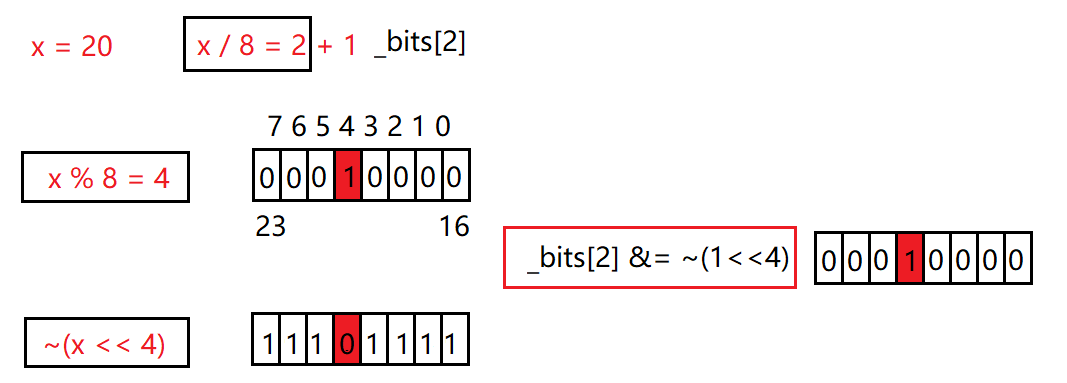
reset的作用是把把x映射的位标记成0，实现规则如下：

1. 通过x / 8计算x在第i个char类型
2. 通过x % 8计算x在char第j个比特位
3. 将1左移 j 位再整体反转后与第 i 个char类型进行与运算即可。

//把x映射的位标记成0
void reset(size_t x)
{
	//x映射的比特位在第几个char对象
	size_t i = x / 8;
	//x在char第几个比特位
	size_t j = x % 8;
	//将1左移 j 位再整体反转后与第 i 个char进行与运算
	_bits[i] &= (~(1 << j));
}

• 3、test

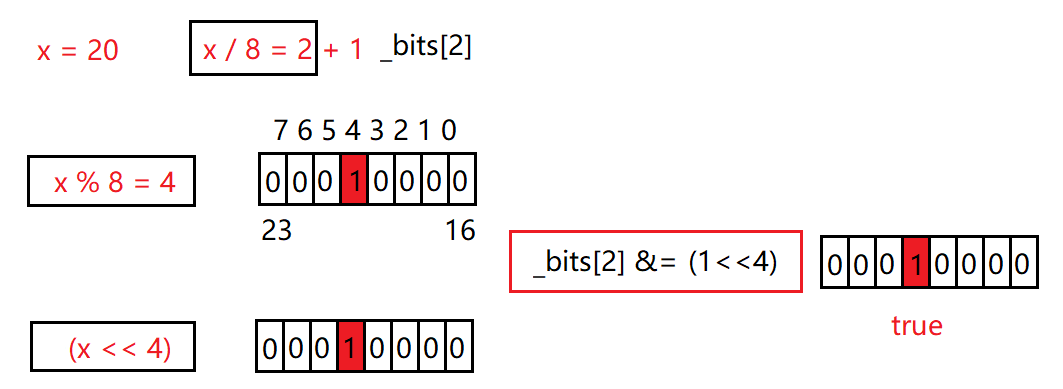
test的作用是判断指定比特位x的状态是否为1，实现规则如下：

1. 通过x / 8计算x在第i个char类型
2. 通过x % 8计算x在char第j个比特位
3. 将1左移 j 位后与第 i 个char类型进行与运算得出结果
4. 若结果非0，则该位被设置，否则该位未被设置

//判断指定比特位x的状态是否为1
bool test(size_t x)
{
	//x映射的比特位在第几个char对象
	size_t i = x / 8;
	//x在char第几个比特位
	size_t j = x % 8;
	//将1左移 j 位后与第 i 个char类型进行与运算得出结果
	return _bits[i] & (1 << j);
}

---

2.3.flip count size

• 1、flip

flip的作用是用于翻转指定位，若指定位为0，翻转后为1，若指定位为1，反转后为0，实现规则如下：

1. 通过x / 8计算x在第i个char类型
2. 通过x % 8计算x在char第j个比特位
3. 将1左移 j 位后与第 i 个char进行按位异或运算^即可。

//翻转指定位x
void flip(size_t x)
{
	//x映射的比特位在第几个char对象
	size_t i = x / 8;
	//x在char第几个比特位
	size_t j = x % 8;
	//将1左移 j 位后与第 i 个char进行按位异或运算^即可。
	_bits[i] ^= (1 << j);
}

• 2、count

count的作用是统计位图中被设计为1的个数，实现规则如下：

1. n = n & (n-1) => 消去n的二进制数中最右边的1
2. n不为零继续执行第一步
3. 执行了几次说明n中有多少个1

//统计set中1的个数
size_t count()
{
	size_t count = 0;
	for (auto e : _bits)
	{
		int n = e;
		while (n)
		{
			n = n & (n - 1);
			count++;
		}
	}
	return count;
}

• 3、size

size的作用是获取位图中可以容纳位N的个数

//获取位图中可以容纳位N的个数
size_t size()
{
	return N;
}

---

2.4.none any all

• 1、none

none的作用是遍历每一个char，如果全为0，则none返回true。

//判断所有比特位若无置为1，返回true
bool none()
{
	//遍历每个char
	for (auto e : _bits)
	{
		if (e != 0)//说明有位被置为1，返回false
			return false;
	}
	return true;//说明全为0，返回true
}

• 2、any

any的作用判断位图中是否有位被置为1，若有则返回true，这其实和none的作用刚好相反，因此我们直接复用none即可。

//判断位图中是否有位被置为1，若有则返回true
bool any()
{
	return !none();
}

• 3、all

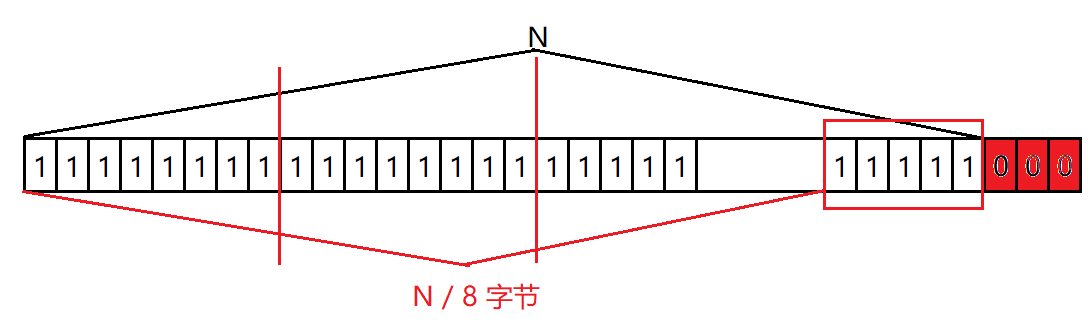
all的作用是判断位图中是否所有的位都被置为1，注意这里的特殊性，先前开辟空间时我们为了避免出现N/8不能整除的情况，特地在resize时多开了一个char类型（8比特）的空间，这8比特里面只有前N%8个比特位才是有效的（剩下的都是多开的空间），因此all函数需要分情况讨论。

1. 先检查前n-1个char的二进制是否为全1。
2. 再检查最后一个char的前N%8个比特位是否为全1。

//全部NUM个bit位被set返回true
bool all()
{
	size_t size = _bits.size();
	//先检查前N-1个char
	for (size_t i = 0; i < size - 1; i++)
	{
		if (~_bits[i] != 0)//取反应该为0，否则取反之前不全为1,返回false
			return false;
	}
	//再检查最后一个char的前 N%8 个位
	for (size_t j = 0; j < N % 8; j++)
	{
		if ((_bits[size - 1] & (1 << j)) == 0)//和test的原理一致
			return false;
	}
	return true;
}

---