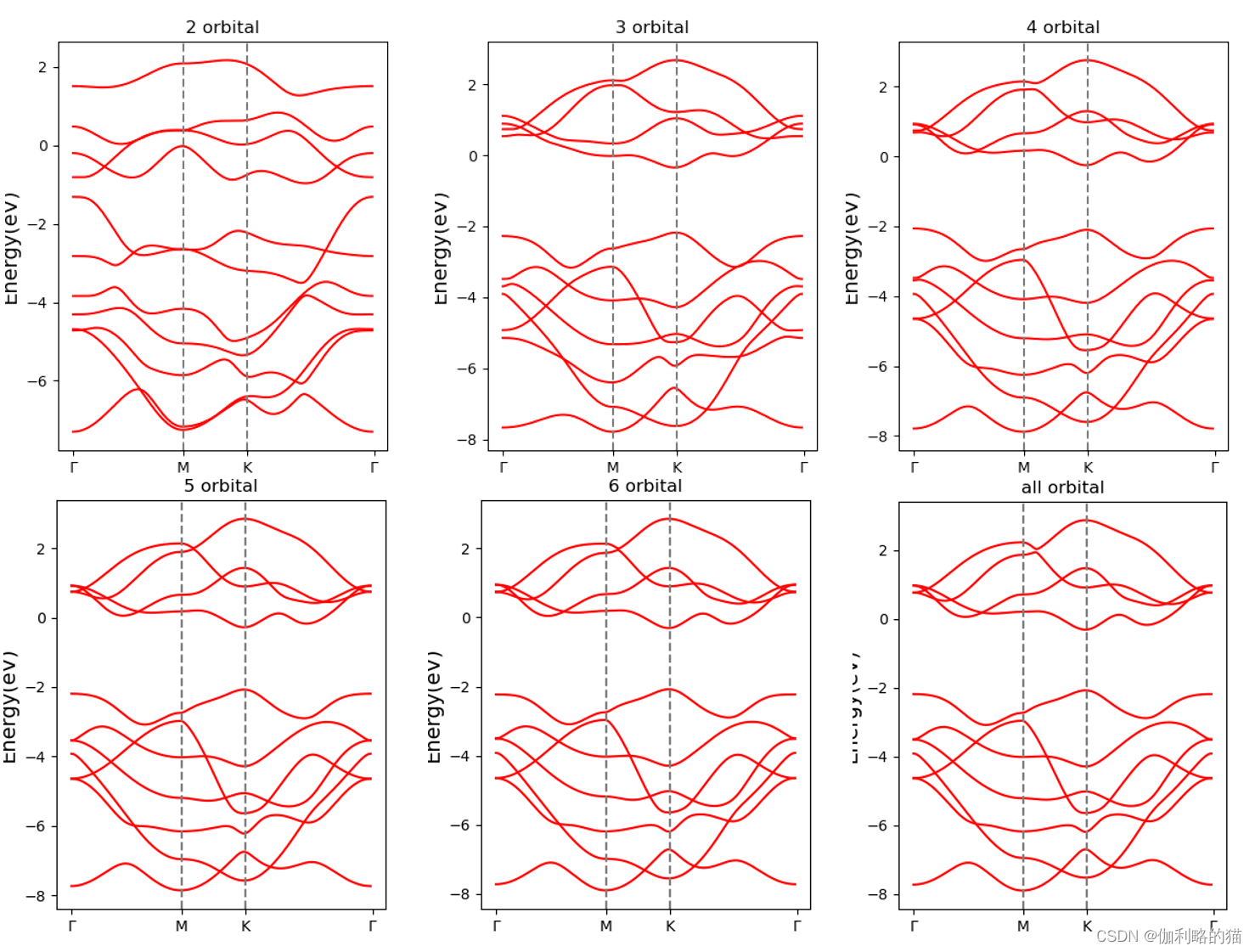
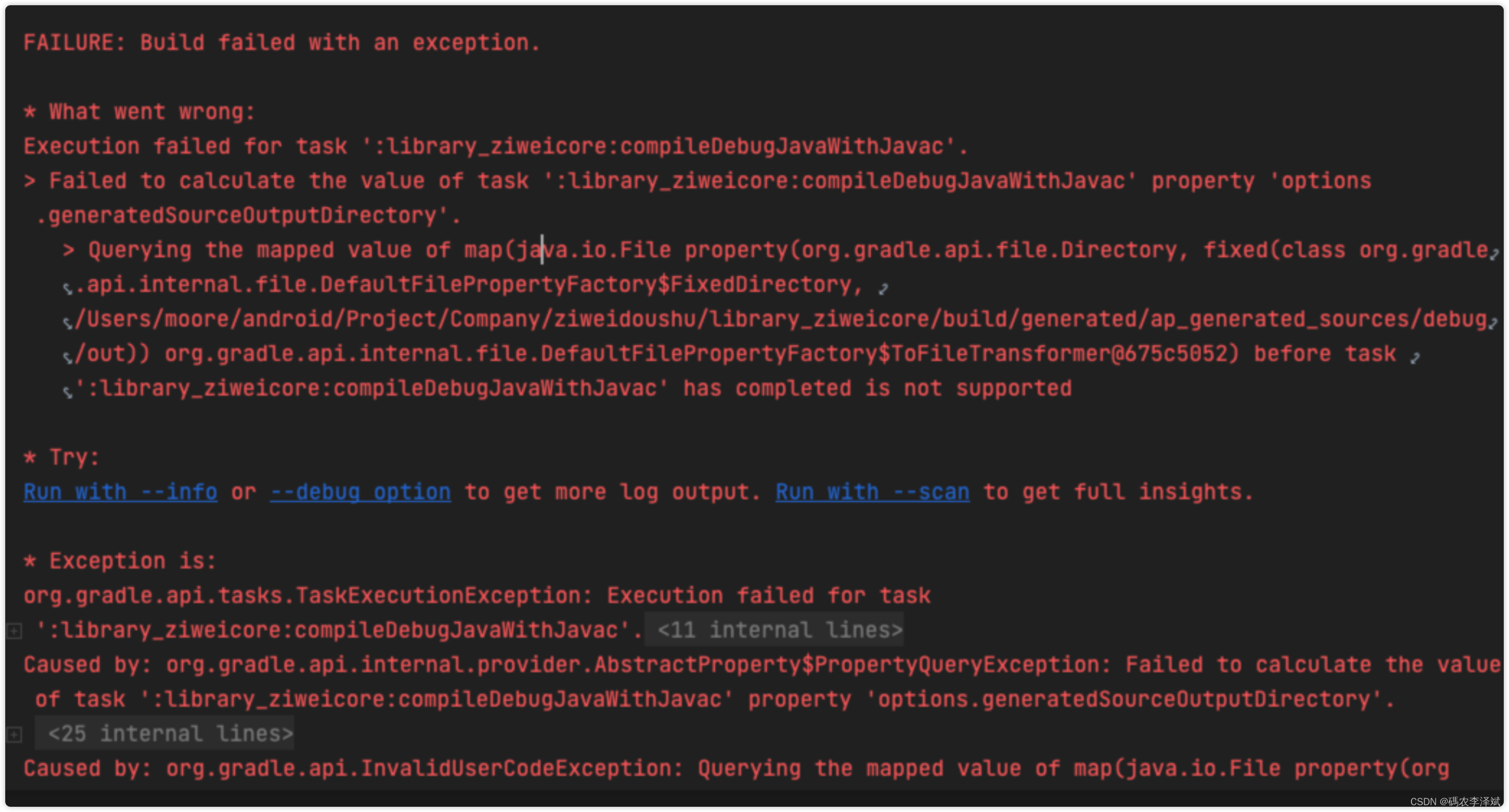
我们知道wannier90可以根据选取TMDs的轨道信息生成详细的hopping energy *_hr.dat文件，选取所有的hopping绘制起来的时候比较简单，但是我们发现取几圈的近似hopping也可以将band表示出来，类似的思想有Pybinding的三带近似（DOI: 10.1103/PhysRevB.88.085433）和Fang的TMDs的紧束缚模型半经验参数近似（DOI: 10.1103/PhysRevB.92.205108）等等。

        我们首先要知道wannier90.dat文件里的数据格式，我们需要的是 类似于

-12   -6    0    1    1    0.000020   -0.000000
-12   -6    0    2    1    0.000000   -0.000000
-12   -6    0    3    1    0.000000    0.000000
-12   -6    0    4    1    0.000004    0.000000
-12   -6    0    5    1    0.000000    0.000000

这样的数据，这里前面三个代表directions[x,y,z] 中间两个代表[fromAtom, toAtom]也就是Rij，后面两个值代表了hopping，代表复数 a+bi 的[a, b]。

        这里的画圈有点类似，也就是根据选择当前原子和目标原子的距离来简要进行阶段，例如下图展示了四层原子（包括[0，0]），可能第三圈的hopping贡献远大于第四圈，所以截取到第三圈即可绘制band。

 这里给出部分示例，选取M的和总的S轨道计算的一个wannier90 *_hr.dat文件，任意选择截取1-10（[0,0]就算了几乎是onsite energy）圈的一个代码，其实取到第5圈就已经比较近似于全部圈层的结果了：

#!/usr/bin python
# -*- encoding: utf-8 -*-
'''
@Author  :   Celeste Young
@File    :   基于fang2015提取MoS2轨道.py    
@Time    :   2023/4/3 14:47  
@E-mail  :   iamwxyoung@qq.com
@Tips    :   
'''

import time
import matplotlib.pyplot as plt
import pandas as pd
# import pybinding as pb
import numpy as np
import functools
import threading


def make_path(k0, k1, *ks, step=0.1):  # kpath 
    k_points = [np.atleast_1d(k) for k in (k0, k1) + ks]
    if not all(k.shape == k_points[0].shape for k in k_points[:1]):
        raise RuntimeError("All k-points must have the same shape")

    k_paths = []
    point_indices = [0]
    for k_start, k_end in zip(k_points[:-1], k_points[1:]):
        num_steps = int(np.linalg.norm(k_end - k_start) // step)
        # k_path.shape == num_steps, k_space_dimensions
        k_path = np.array([np.linspace(s, e, num_steps, endpoint=False)
                           for s, e in zip(k_start, k_end)]).T
        k_paths.append(k_path)
        point_indices.append(point_indices[-1] + num_steps)
    k_paths.append(k_points[-1])

    return np.vstack(k_paths)  # , point_indices)


def isinDirect(v_, hvts):  # 判断是否在所选的directions里，上图的n层
    for vs in hvts:
        if ''.join(v_) == ''.join(list(map(str, vs))):
            return True
    return False


def read_dat(*args, **kwargs):
    with open("data/wannier90_hr_MoS2.dat", "r") as f:
        lines = f.readlines()
    rij = [[[] for col in range(nb)] for row in range(nb)]
    tij = [[[] for col in range(nb)] for row in range(nb)]
    for line in lines:
        ll = line.split()
        if isinDirect(ll[:3], kwargs['hvts']):
            x, y, z, frAt, toAt = list(map(int, ll[:5]))
            t_real, t_image = list(map(float, ll[5:]))
            rij[frAt - 1][toAt - 1].append([x, y, z])
            tij[frAt - 1][toAt - 1].append([t_real + 1j * t_image])
 
    return rij, tij


def plot_rec(*args, **kwargs):  # 绘制布里渊区的积分路径
    fig = plt.figure(figsize=(5, 5))
    ax = plt.axes()
    ax.arrow(0, 0, a1[0], a1[1], length_includes_head=False, head_width=0.05, fc='b', ec='k')
    ax.arrow(0, 0, a2[0], a2[1], length_includes_head=False, head_width=0.05, fc='b', ec='k')
    ax.arrow(0, 0, b1[0], b1[1], length_includes_head=False, head_width=0.05, fc='r', ec='red')
    ax.arrow(0, 0, b2[0], b2[1], length_includes_head=False, head_width=0.05, fc='r', ec='red')
    ax.plot([0, Middle[0], K1[0], 0], [0, Middle[1], K1[1], 0])
    ax.scatter([0, Middle[0], K1[0], 0], [0, Middle[1], K1[1], 0])
    ax.set_xlim(-1, 4)
    ax.set_ylim(-2, 4)
    ax.grid()
    plt.show()


def phase(*args, **kwargs):
    rij = kwargs['hr']
    wk = kwargs['wk']
    R_vec = 0
    for ii in range(3):
        R_vec += rij[ii] * basis_vector[ii]
    inner_product = np.dot(R_vec, wk)
    return np.exp(1j * inner_product)


def Hamham(wak, tij, rij):
    h = np.zeros((nb, nb), dtype=complex)
    for ii in range(nb):
        for jj in range(nb):
            for vij in range(len(rij[ii][jj])):
                hr = rij[ii][jj][vij]
                h[ii, jj] = h[ii, jj] + tij[ii][jj][vij][0] * phase(hr=hr, wk=wak)
    return h


def get_sphere(*args, **kwargs):  #获取需要的层的directions，传入参数n=[1,11)
    sp_ = args[0]
    spDict = {}
    # sp = 0
    sp0 = [[0, 0, 0]]
    spDict['sp0'] = sp0
    # sp = 1 >> 3*2
    sp1 = [[1, 0, 0], [1, 1, 0], [0, 1, 0]]
    sp1 = sp1 + [list(-np.array(sp1[i])) for i in range(len(sp1))]
    spDict['sp1'] = sp1
    # sp = 2 >> 3*2
    sp2 = [[2, 1, 0], [1, 2, 0], [-1, 1, 0]]
    sp2 = sp2 + [list(-np.array(sp2[i])) for i in range(len(sp2))]
    spDict['sp2'] = sp2
    # sp = 3 >> 3*2
    sp3 = [[2, 0, 0], [2, 2, 0], [0, 2, 0]]
    sp3 = sp3 + [list(-np.array(sp3[i])) for i in range(len(sp3))]
    spDict['sp3'] = sp3
    # sp = 4 >> 6*2
    sp4 = [[3, 1, 0], [3, 2, 0], [2, 3, 0], [1, 3, 0], [-1, 2, 0], [-2, 1, 0]]
    sp4 = sp4 + [list(-np.array(sp4[i])) for i in range(len(sp4))]
    spDict['sp4'] = sp4
    # sp = 5 >> 3*2
    sp5 = [[3, 0, 0], [3, 3, 0], [0, 3, 0]]
    sp5 = sp5 + [list(-np.array(sp5[i])) for i in range(len(sp5))]
    spDict['sp5'] = sp5
    # sp = 6 >> 3*2
    sp6 = [[4, 2, 0], [2, 4, 0], [-2, 2, 0]]
    sp6 = sp6 + [list(-np.array(sp6[i])) for i in range(len(sp6))]
    spDict['sp6'] = sp6
    # sp = 7 >> 3*2
    sp7 = [[4, 1, 0], [4, 3, 0], [3, 4, 0], [1, 4, 0], [-1, 3, 0], [-3, 1, 0]]
    sp7 = sp7 + [list(-np.array(sp7[i])) for i in range(len(sp7))]
    spDict['sp7'] = sp7
    # sp = 8 >> 3*2
    sp8 = [[4, 0, 0], [4, 4, 0], [0, 4, 0]]
    sp8 = sp8 + [list(-np.array(sp8[i])) for i in range(len(sp8))]
    spDict['sp8'] = sp8
    sp9 = [[5, 2, 0], [5, 3, 0], [2, 5, 0], [3, 5, 0], [-2, 3, 0], [-3, 2, 0]]
    sp9 = sp9 + [list(-np.array(sp9[i])) for i in range(len(sp9))]
    spDict['sp9'] = sp9
    sp10 = [[5, 1, 0], [5, 4, 0], [1, 5, 0], [4, 5, 0], [-1, 4, 0], [-4, 1, 0]]
    sp10 = sp10 + [list(-np.array(sp10[i])) for i in range(len(sp10))]
    spDict['sp10'] = sp10
    if sp_ == 0:
        return sp0

    tmpl = []
    for i in range(sp_):
        tmpl += [j for j in spDict['sp%d' % i]]
    return tmpl


def selectAllOrbital():
    with open("data/wannier90_hr_MoS2.dat", "r") as f:
        lines = f.readlines()
    rij = [[[] for col in range(nb)] for row in range(nb)]
    tij = [[[] for col in range(nb)] for row in range(nb)]
    for line in lines:
        ll = line.split()
        if len(ll) == 7:
            x, y, z, frAt, toAt = list(map(int, ll[:5]))
            t_real, t_image = list(map(float, ll[5:]))
            rij[frAt - 1][toAt - 1].append([x, y, z])
            tij[frAt - 1][toAt - 1].append([t_real + 1j * t_image])
    hamilton = functools.partial(Hamham, tij=tij, rij=rij)
    idx = 0
    result = np.zeros([len(path), 11])
    for kxy in range(len(path)):
        k = np.r_[path[kxy], [0]]
        w, t = np.linalg.eig(hamilton(k))
        w = list(w)
        w.sort()
        result[idx, :] = np.real(w)  # 将本征值进行保存
        idx += 1
    xk = [0, rt3, rt3 + 1, rt3 + 3]
    kk = np.linspace(0, 4.7, num=len(path))  # 作为x轴，使其和本征值矩阵每一列的y的值个数相同
    plt.figure(figsize=(4, 5))
    plt.plot(kk, result, c="r")
    plt.xticks(xk, ["Γ", "M", "K", "Γ"])
    plt.ylabel("Energy(eV)", fontsize=14)
    plt.axvline(rt3, color='gray', linestyle='--')
    plt.axvline(rt3 + 1, color='gray', linestyle='--')
    plt.title('all orbital')
    plt.savefig('all orbital.png')
    print('Saved all orbital figure!')


def selectOrbital(orbi):
    print('started %d/%d' % (orbi, 10))
    hvts = get_sphere(orbi)
    result = np.zeros([len(path), 11])  # 解的矩阵
    Rij, Tij = read_dat(hvts=hvts)
    hamilton = functools.partial(Hamham, tij=Tij, rij=Rij)
    idx = 0
    for kxy in range(len(path)):
        k = np.r_[path[kxy], [0]]
        w, t = np.linalg.eig(hamilton(k))
        w = list(w)
        w.sort()
        result[idx, :] = np.real(w)  # 将本征值进行保存
        idx += 1
    xk = [0, rt3, rt3 + 1, rt3 + 3]
    kk = np.linspace(0, 4.7, num=len(path))  # 作为x轴，使其和本征值矩阵每一列的y的值个数相同
    plt.figure(figsize=(4, 5))
    plt.plot(kk, result, c="r")
    plt.xticks(xk, ["Γ", "M", "K", "Γ"])
    plt.ylabel("Energy(eV)", fontsize=14)
    plt.axvline(rt3, color='gray', linestyle='--')
    plt.axvline(rt3 + 1, color='gray', linestyle='--')
    plt.title('%d orbital' % orbi)
    plt.savefig('%d orbital.png' % orbi)
    print('finish %d/%d' % (orbi, 10))


if __name__ == '__main__':
    # start here
    time1 = time.time()
    nb = 11  # number of bands
    a = 3.160  # 3.18
    c = 12.29  # distance of layers
    dxx = 3.13  # distance of orbital X-X
    dxm = 2.41  # distance of orbital X-M
    # constant checked
    rt3 = 3 ** 0.5
    pi = np.pi
    a1 = a * np.array([rt3 / 2, -1 / 2, 0])
    a2 = a * np.array([0, 1, 0])
    a3 = a * np.array([0, 0, 5])
    basis_vector = np.array([a1, a2, a3])

    b1 = 2 * pi / a * np.array([1 / rt3, 1])
    b2 = 4 * pi / a / rt3 * np.array([1, 0])

    Gamma = np.array([0, 0])
    Middle = 1 / 2 * b1
    K1 = 1 / 3 * (2 * b1 - b2)
    K2 = -1 / 3 * (2 * b1 - b2)
    # plot_rec()
    path = make_path(Gamma, Middle, K1, Gamma, step=0.01)

    # selectAllOrbital()  # 这里取消注释会绘制总的圈层的band

    for orb in range(1, 11):
        selectOrbital(orbi=orb)


    time2 = time.time()
    print('>> Finished, use time %d s' % (time2 - time1))

附上我的hr.dat的结果图: