[牛客复盘] 牛客小白月赛70 20230407
- 一、本周周赛总结
- A、 小d和答案修改
- 2. 思路分析
- 3. 代码实现
- B、小d和图片压缩
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- C、小d和超级泡泡堂
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- D、小d和孤独的区间
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- E、小d的博弈
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- F、小d和送外卖
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、参考链接
一、本周周赛总结
- 第一次打小白月赛,据说比较简单,但还是有两道没做出来。
- A 模拟。
- B 模拟。
- C FloodFill。
- D 前缀和+哈希。
- E 博弈 打表/贪心。
- F 树上背包/有依赖的背包,注意卡常。

A、 小d和答案修改

2. 思路分析
按题意模拟即可。
3. 代码实现
import sys
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
# ms
def solve():
n, m = RI()
g = []
for _ in range(n):
g.append(RILST())
for i in range(0, n, 2):
for j in range(0, m, 2):
c = (g[i][j] + g[i + 1][j] + g[i + 1][j + 1] + g[i][j + 1]) // 4
print(c, end=' ')
print()
if __name__ == '__main__':
solve()
B、小d和图片压缩
链接: 小d和图片压缩
1. 题目描述
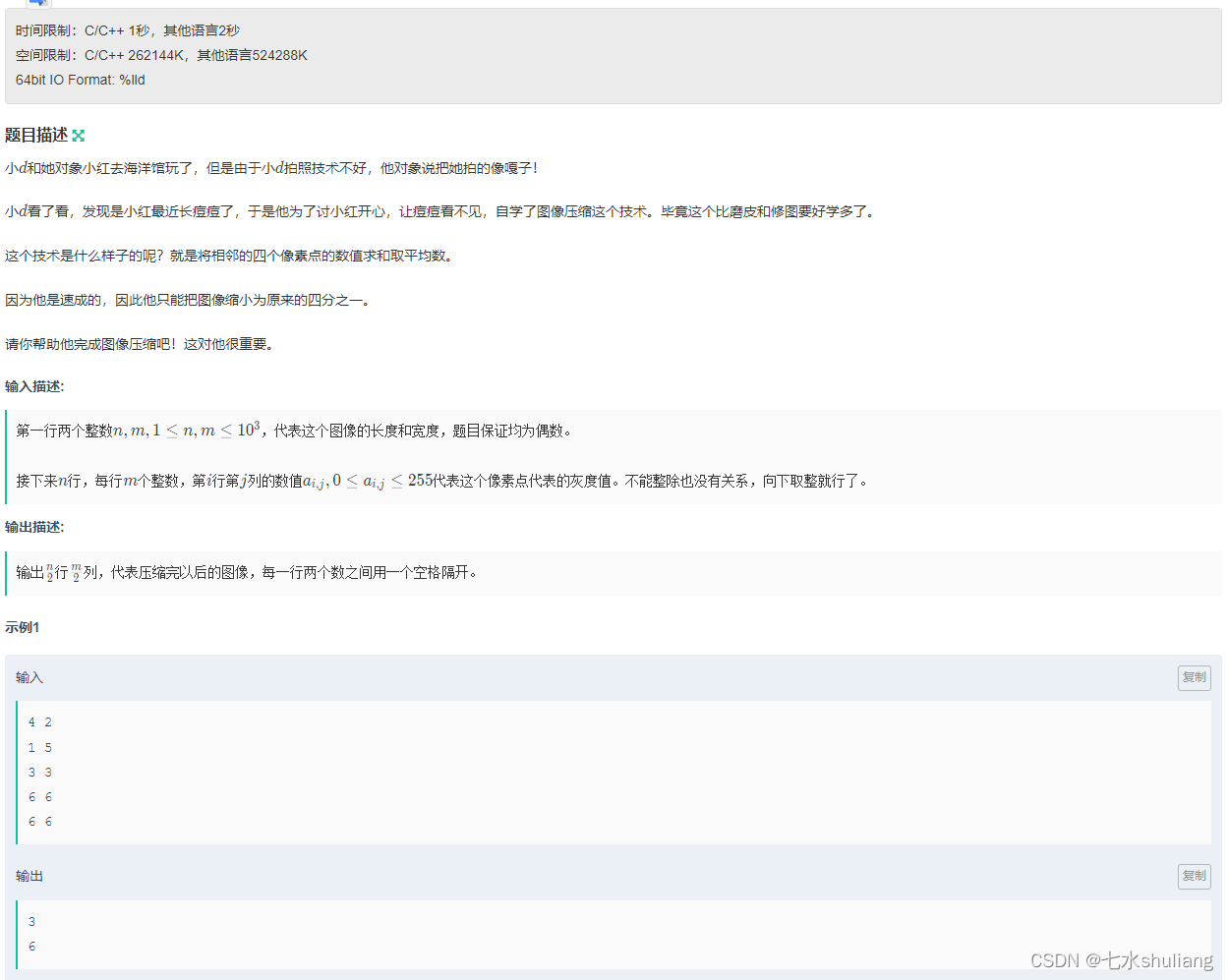
2. 思路分析
模拟。
3. 代码实现
def solve():
n, m = RI()
g = []
for _ in range(n):
g.append(RILST())
for i in range(0, n, 2):
for j in range(0, m, 2):
c = (g[i][j] + g[i + 1][j] + g[i + 1][j + 1] + g[i][j + 1]) // 4
print(c, end=' ')
print()
C、小d和超级泡泡堂
链接: 小d和超级泡泡堂
1. 题目描述
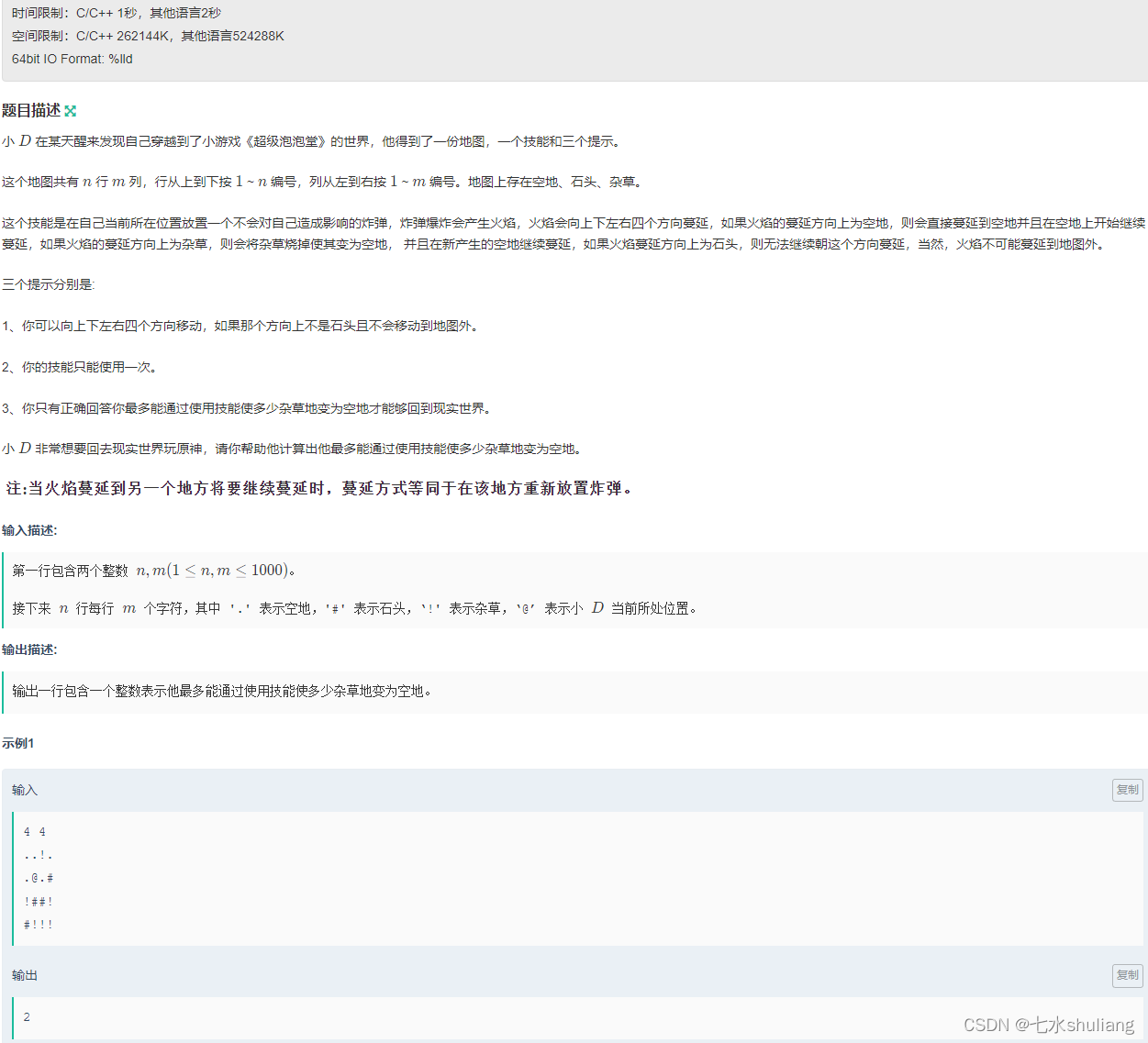
2. 思路分析
- floodfiill的时候计数路上遇到的草即可。
- 注意访问后把位置变成石头防止重复访问。
3. 代码实现
def solve():
n, m = RI()
g = []
start = (0, 0)
for i in range(n):
s, = RS()
g.append(list(s))
if '@' in s:
j = s.index('@')
start = (i, j)
g[i][j] = '#'
ans = 0
q = deque([start])
while q:
x, y = q.popleft()
for a, b in (x - 1, y), (x + 1, y), (x, y + 1), (x, y - 1):
if 0 <= a < n and 0 <= b < m and g[a][b] != '#':
if g[a][b] == '!':
ans += 1
g[a][b] = '#'
q.append((a, b))
print(ans)
D、小d和孤独的区间
链接: 小d和孤独的区间
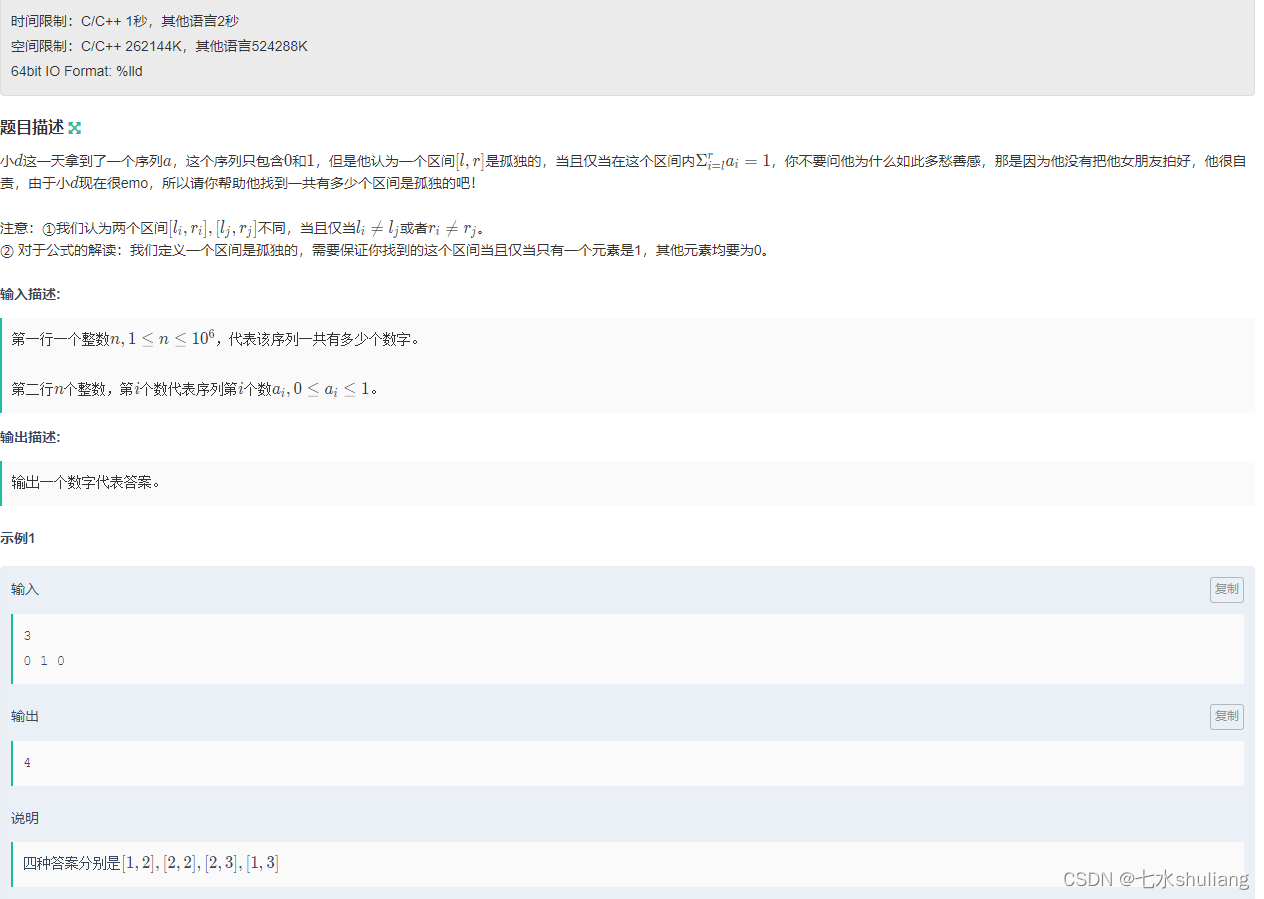
1. 题目描述
2. 思路分析
- 典中典中典,题目中只包含01甚至是没用的。
- 计算前缀和,遍历的时候用哈希表记录每个前缀和出现的次数。
- 当遍历到i时,s[i]-t = 1,t = s[i]-1,找到前边有几个t,则以i为右端点的合法区间就有几个。
3. 代码实现
def solve():
n, = RI()
a = RILST()
p = Counter([0])
s = ans = 0
for v in a:
s += v
ans += p[s - 1]
p[s] += 1
print(ans)
E、小d的博弈
链接: 小d的博弈
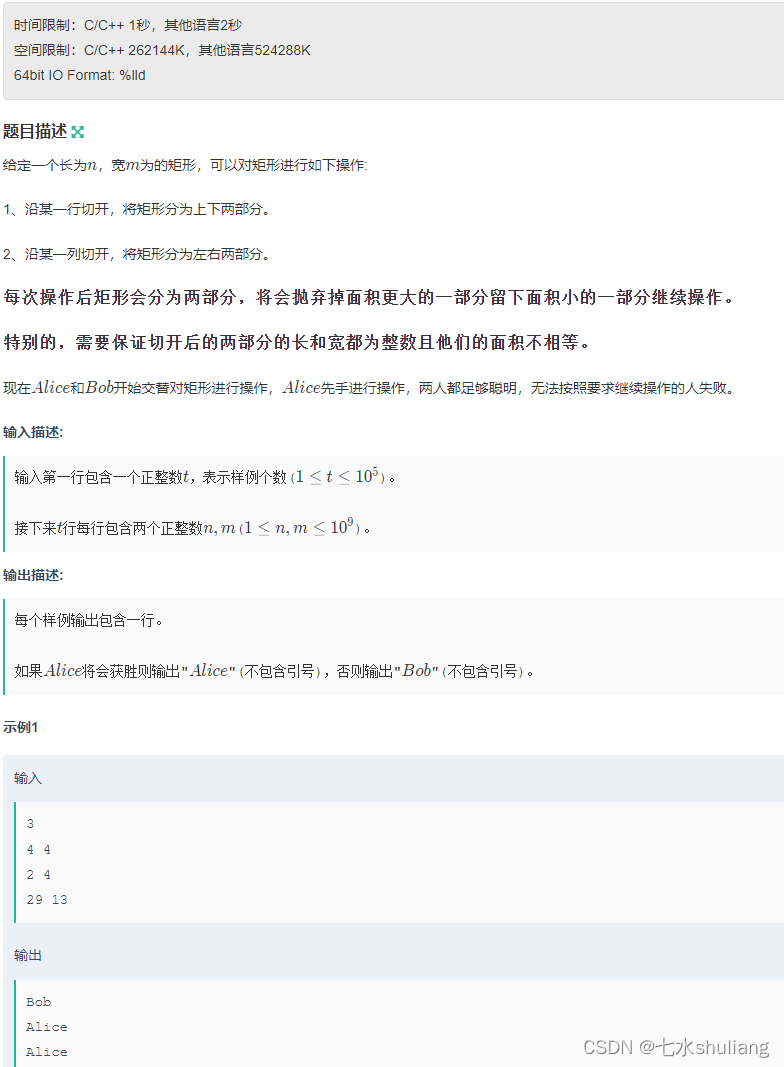
1. 题目描述
2. 思路分析
- 看到博弈上来就写了个记忆化搜索,很快啊 ,就TLE了。代码如下,看状态数和nm的范围显然要T:
@lru_cache(None)
def dfs(m, n):
if m <= 2 and n <= 2:
return False
if m <= 2 or n <= 2:
return True
for i in range(1, (m + 1) // 2):
if not dfs(i, n):
return True
for j in range(1, (n + 1) // 2):
if not dfs(m, j):
return True
return False
- 把这个表打出来,形如(注意是nm从1开始):
-
- 看这美妙的规律,2,、4、8…的增长似乎代表着什么,每次增长2的幂,那么发现把这个数+1,求二进制长度,俩数二进制长度相同,bob就赢,否则alice赢。(对应代码里solve)
- 不按规律做题的话,其实是把每条边以最大次数切割,看看分别能切多少次,如果两边次数相同,则bob赢。对应代码里solve1
- 这是因为:bob总可以按照alice的切法,使切完后依然边数相同,那么bob必是切最后一刀的。
3. 代码实现
# Problem: 小d的博弈
# Contest: NowCoder
# URL: https://ac.nowcoder.com/acm/contest/53366/E
# Memory Limit: 524288 MB
# Time Limit: 2000 ms
import sys
from functools import lru_cache
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
PROBLEM = """
"""
@lru_cache(None)
def dfs(m, n):
if m <= 2 and n <= 2:
return False
if m <= 2 or n <= 2:
return True
for i in range(1, (m + 1) // 2):
if not dfs(i, n):
return True
for j in range(1, (n + 1) // 2):
if not dfs(m, j):
return True
return False
# 603 ms
def solve1():
n, m = RI()
y = x = 0
while n > 2:
n = (n - 1) // 2
x += 1
while m > 2:
m = (m - 1) // 2
y += 1
if x != y:
print('Alice')
else:
print('Bob')
# 573 ms
def solve():
n, m = RI()
if (n + 1).bit_length() != (m + 1).bit_length():
print('Alice')
else:
print('Bob')
if __name__ == '__main__':
t, = RI()
for _ in range(t):
solve()
# for i in range(1,40):
# for j in range(1,40):
# print(int(dfs(i,j)), end=' ')
# print()
F、小d和送外卖
链接: 小d和送外卖
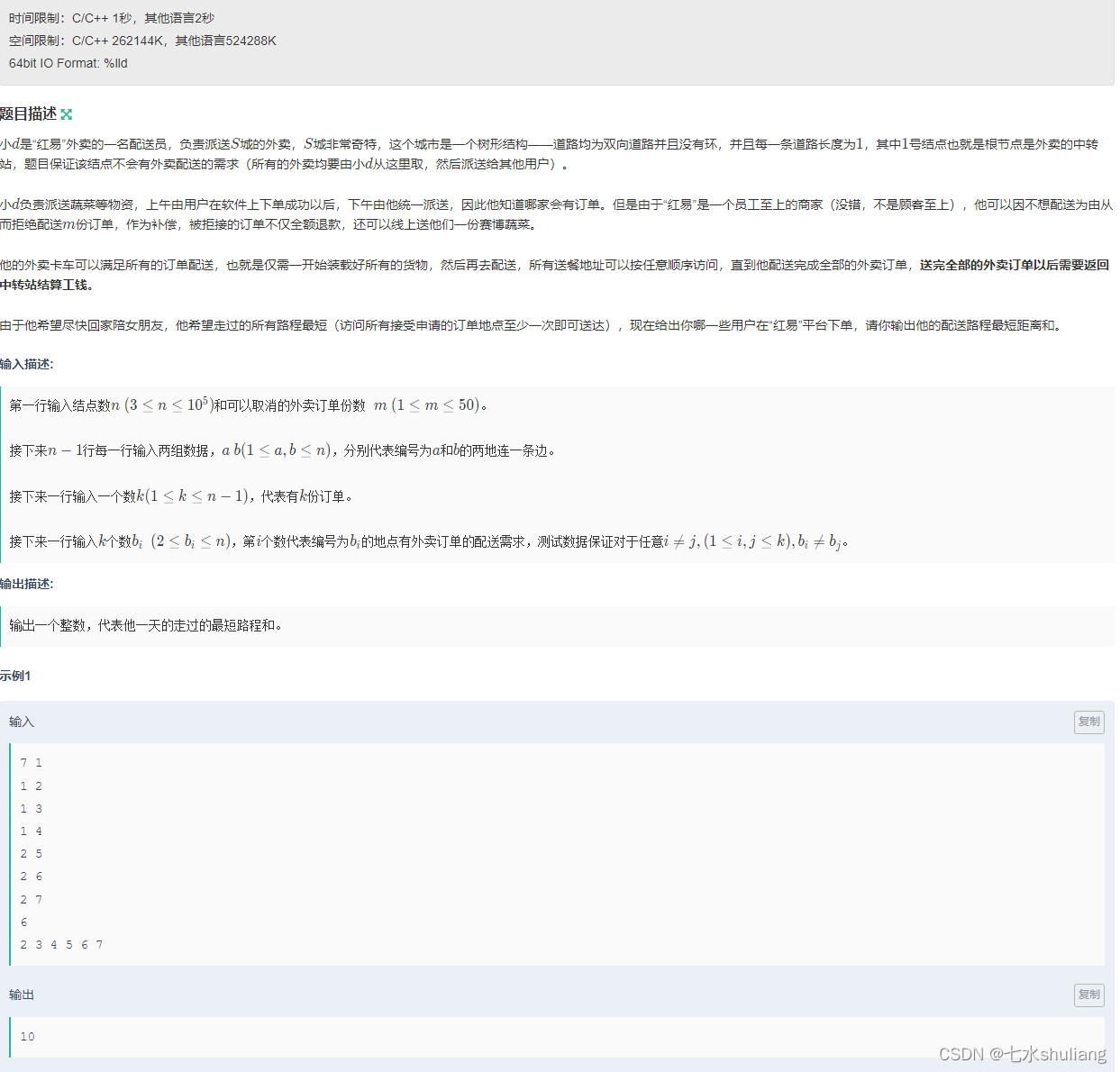
1. 题目描述
2. 思路分析
- 这是我第二次做树形背包,第一次还是做acw10有依赖的背包。不同在于:
- acw10是必须选父节点才能选子节点。那么向下递归之前先把父节点选上,更新dp数组,且向下传递时,背包容量减小。
- 本题是必须选子节点才能选父节点。需要先处理子树后,再尝试把整颗子树包括父节点一起选上。
- 看到m<=50的份数就可以想到背包了。这里做一下转化:选择取消哪m份外卖能使总距离和最短 等价与 :选择取消哪m份外卖能使节省的总距离和最长。
- 转换后,只需要考虑子树即可。当然,前提是先计算出不取消的话需要跑的总距离。
- 可以先用一个dfs后根遍历计算出每颗子树里,包含几个外卖订单,用yes[i]表示;同时,如果跑完子树里所有订单,需要走的节点数,用cnt[i]表示。
- 我们发现,需要走的路程=边数*2=(节点数-1)*2
- 接下来,只需要计算出选m个订单取消,可以最多少走多少个节点即可。用树形背包解决。
- 对每个子树,分别定义f = [0] + [-inf] * m,其中f[i]表示在这颗子树下,取消i个订单,最多少走几个节点。dfs结束后返回f。
- 我们dfs u的每个子树v,令p=dfs(v),根据定义,p是v子树取消i订单的每种情况,而这颗子树我们可以选p里的任意一种情况或不选。那么p对于u来说就是一个分组背包的一个组。遍历每个子树作为物品更新f即可。
- 用完子树后,尝试是否可以把u这颗子树整个拿掉,前提是这颗子树里的订单yes<=m,更新f[yes]=cnt,即取消yes个订单,少走个子树的节点。背包转移就结束了。
- 最后省的最大值就是max§。这里由于是后根遍历,每次计算完都是进父节点用,直接用一个全局遍历储存一个,滚动赋值即可。
- 最后答案是
(cnt[0] - 1 - max(p)) * 2。即根节点的原本路程-省的路程。
- 吐槽卡常,背包转移时如果不提前break会TLE。
- 另外我试图写了bfs版本,先根遍历顺序后,逆序处理。会更慢一些。猜测是因为:由于计算时不能保证子树处理完了立马给父节点用,因此需要全局储存每个子树的f,内存会用的多些。
3. 代码实现
# Problem: 小d和送外卖
# Contest: NowCoder
# URL: https://ac.nowcoder.com/acm/contest/53366/F
# Memory Limit: 524288 MB
# Time Limit: 2000 ms
import sys
from collections import deque
from math import inf
from types import GeneratorType
RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')
MOD = 10 ** 9 + 7
PROBLEM = """
"""
def bootstrap(f, stack=[]):
def wrappedfunc(*args, **kwargs):
if stack:
return f(*args, **kwargs)
else:
to = f(*args, **kwargs)
while True:
if type(to) is GeneratorType:
stack.append(to)
to = next(to)
else:
stack.pop()
if not stack:
break
to = stack[-1].send(to)
return to
return wrappedfunc
# 1455 ms
def solve1():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v = RI()
u -= 1
v -= 1
g[u].append(v)
g[v].append(u)
k, = RI()
a = RILST()
if k <= m:
return print(0)
s = set(x - 1 for x in a)
# print(s)
cnt = [0] * n # 如果要送完这个子树的所有订单,要访问多少个节点;答案是边数*2,即(cnt[i]-1)*2
yes = [0] * n # 每个子树下共有几个订单
p = [] # 子树的分组背包,p[i]代表如果这个子树里退i个单,最多能省几个需要访问的节点
@bootstrap
def dfs(u, fa):
f = [0] + [-inf] * m # 当前子树如果一个都不退,就不能省节点
yes[u] = int(u in s) # 如果本节点有订单,则订单数+1
for v in g[u]:
if v == fa: continue
yield dfs(v, u)
if yes[v]: # 如果子树有订单,要累计过来,且路过的节点也要累计
yes[u] += yes[v]
cnt[u] += cnt[v]
for j in range(m, 0, -1):
for v, w in enumerate(p):
if v <= j:
f[j] = max(f[j], f[j - v] + w)
else:
break
if yes[u]: # 如果这个子树有订单,则这个加上这个节点
cnt[u] += 1
if yes[u] <= m: # 如果这个子树下的所有订单不超过m,则可以尝试剪掉整个子树。
f[yes[u]] = cnt[u]
p[:] = f[:]
yield
dfs(0, -1)
# print(cnt)
# print(yes)
print((cnt[0] - 1 - max(p)) * 2)
# 1447ms ms
def solve2():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v = RI()
u -= 1
v -= 1
g[u].append(v)
g[v].append(u)
k, = RI()
a = RILST()
if k <= m:
return print(0)
s = set(x - 1 for x in a)
# print(s)
cnt = [0] * n # 如果要送完这个子树的所有订单,要访问多少个节点;答案是边数*2,即(cnt[i]-1)*2
yes = [0] * n # 每个子树下共有几个订单
@bootstrap
def dfs(u, fa):
yes[u] = int(u in s)
for v in g[u]:
if v == fa: continue
yield dfs(v, u)
if yes[v]:
yes[u] += yes[v]
cnt[u] += cnt[v]
if yes[u]:
cnt[u] += 1
yield
dfs(0, -1)
# print(cnt)
# print(yes)
p = []
@bootstrap
def dfs2(u, fa):
f = [0] + [-inf] * m
for v in g[u]:
if v == fa: continue
yield dfs2(v, u)
for j in range(m, 0, -1):
for v, w in enumerate(p):
if v <= j:
f[j] = max(f[j], f[j - v] + w)
else:
break
if yes[u] <= m:
f[yes[u]] = cnt[u]
# print(u, f)
p[:] = f[:]
yield
dfs2(0, -1)
print((cnt[0] - 1 - max(p)) * 2)
# ms
def solve():
n, m = RI()
g = [[] for _ in range(n)]
for _ in range(n - 1):
u, v = RI()
u -= 1
v -= 1
g[u].append(v)
g[v].append(u)
k, = RI()
a = RILST()
if k <= m:
return print(0)
s = set(x - 1 for x in a)
# print(s)
cnt = [0] * n # 如果要送完这个子树的所有订单,要访问多少个节点;答案是边数*2,即(cnt[i]-1)*2
yes = [0] * n # 每个子树下共有几个订单
pp = [[] for _ in range(n)]
fas = [-1] * n
order = []
q = deque([0])
while q:
u = q.popleft()
order.append(u)
for v in g[u]:
if v == fas[u]: continue
fas[v] = u
q.append(v)
for u in order[::-1]:
yes[u] = int(u in s)
f = [0] + [-inf] * m
for v in g[u]:
if v == fas[u]: continue
if yes[v]:
yes[u] += yes[v]
cnt[u] += cnt[v]
p = pp[v]
for j in range(m, 0, -1):
for v, w in enumerate(p):
if v <= j:
f[j] = max(f[j], f[j - v] + w)
else:
break
if yes[u]:
cnt[u] += 1
if yes[u] <= m:
f[yes[u]] = cnt[u]
pp[u] = f
print((cnt[0] - 1 - max(pp[0])) * 2)
if __name__ == '__main__':
solve()