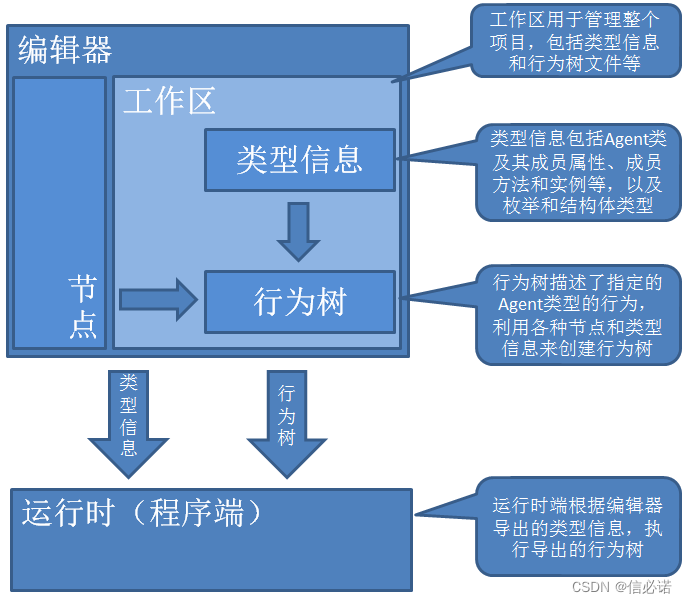
题目描述

给定两个排序后的数组 A 和 B，其中 A 的末端有足够的缓冲空间容纳 B。编写一个方法，将 B 合并入 A 并排序。

初始化 A 和 B 的元素数量分别为 m 和 n。

示例:

输入:
A = [1,2,3,0,0,0], m = 3
B = [2,5,6], n = 3
输出: [1,2,2,3,5,6]

说明:

A.length == n + m

解题思路与代码

这道题的难度是简单题。可以说没什么太多的可讲的。

方法一：使用sort函数

思路就是用b的元素将a中的0替换掉，然后sort()，重新排序一下就好，可以说是没有什么技术含量的啦。

具体代码如下：

class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        if(B.empty()) return;
        int point = 0;
        for(int i = 0; i < A.size(); ++i){
            if(A[i] == 0 && point < B.size()){
                A[i] = B[point];
                ++point;
            }
        }
        sort(A.begin(),A.end());
    }
};

复杂度分析

时间复杂度：

首先，这个解决方案中的 for 循环遍历了 A 的所有元素。因为 A 的长度为 m+n，所以这个循环的时间复杂度是 O(m+n)。
接下来，sort 函数对 A 进行排序。在 C++ 中，sort 函数的平均时间复杂度是 O(N*log(N))，这里 N 是需要排序的数组长度，也就是 A 的长度，即 m+n。因此，排序的时间复杂度是 O((m+n)*log(m+n))。
因此，这个解决方案的总时间复杂度是 O((m+n) + (m+n)*log(m+n))，可以简化为 O((m+n)*log(m+n))。

空间复杂度：

这个解决方案在原数组 A 上进行了操作，并没有使用额外的空间来存储合并后的结果。所以，空间复杂度为 O(1)。

小总结

这种做法其实没有完全用到题目给我们的一些条件。比如说，A 与 B 是两个有序数组。所以在性能上，是比较差的。

方法二：双指针（多指针）从后向前遍历

这里我其实用到了3个指针，但我感觉只要是超过了2个指针的题，大家都默认叫双指针，我觉得其实不是很准确，其实是三指针解决的这道题。我也不想标新立异，那就叫双指针的题好啦。

这道题主要的解题思路是这样的。我们将一个指针指向A数组的除0以外的最后一个元素，另一个指针指向B数组最后一个元素，最后一个指针指向A数组最后一个元素。使用while循环从后向前遍历。

具体实现，请看代码：

class Solution {
public:
    void merge(vector<int>& A, int m, vector<int>& B, int n) {
        int pA = m - 1;
        int pB = n - 1;
        int pEnd = n + m - 1;
        while(pA >= 0 && pB >= 0){
            if(B[pB] > A[pA]){
                A[pEnd] = B[pB];
                --pB;
            }else{
                A[pEnd] = A[pA];
                --pA;
            }
            --pEnd;
        }
        while(pB >= 0){
            A[pEnd] = B[pB];
            --pB;
            --pEnd;
        }
    }
};