递归算法

程序调用自身的编程技巧称为递归。—百度百科

我们可以这样理解递归：

递归：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，你继续打开它。若干次之后，你打开面前的门后，发现只有一间屋子，没有门了。然后，你开始原路返回，每走回一间屋子，你数一次，走到入口的时候，你可以回答出你到底用这你把钥匙打开了几扇门。

此时是不是有人不禁要问这难道不是循环吗 ？？已晕·····

循环：你打开面前这扇门，看到屋里面还有一扇门。你走过去，发现手中的钥匙还可以打开它，你推开门，发现里面还有一扇门，你继续打开这扇门，一直这样继续下去直到打开所有的门。但是，入口处的人始终等不到你回去告诉他答案。

通过上面的比喻相信我们已经可以发现递归的精髓（思想）是什么了

递归的思想

正如上面所描述的场景，递归就是==有去（递去）有回（归来）==
“有去”是指：递归问题必须可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决，就像上面例子中的钥匙可以打开后面所有门上的锁一样；
“有回”是指 : 这些问题的演化过程是一个从大到小，由近及远的过程，并且会有一个明确的终点(临界点)，一旦到达了这个临界点，就不用再往更小、更远的地方走下去。最后，从这个临界点开始，原路返回到原点，原问题解决。

递归三要素

明确递归终止条件

我们知道，递归就是有去有回，既然这样，那么必然应该有一个明确的临界点，程序一旦到达了这个临界点，就不用继续往下递去而是开始实实在在的归来。换句话说，该临界点就是一种简单情境，可以防止无限递归。

给出递归终止时的处理方法

我们刚刚说到，在递归的临界点存在一种简单情境，在这种简单情境下，我们应该直接给出问题的解决方案。一般地，在这种情境下，问题的解决方案是直观的、容易的。

提取重复的逻辑，缩小问题规模

我们在阐述递归思想内涵时谈到，递归问题必须可以分解为若干个规模较小、与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决。从程序实现的角度而言，我们需要抽象出一个干净利落的重复的逻辑，以便使用相同的方式解决子问题。

递归的编程模型

模型一 ：在递去的过程中解决问题

function recursion(大规模){ 
if (end_condition){ 
// 明确的递归终止条件 end; 
// 简单情景 
}
else{ 
// 在将问题转换为子问题的每一步，解决该步中剩余部分的问题 solve; 
// 递去 recursion(小规模); // 递到最深处后，不断地归来 } 
}

模型二 ：在归来的过程中解决问题

function recursion(大规模){ 
if (end_condition){ 
// 明确的递归终止条件 end;
// 简单情景 
}
else{ 
// 先将问题全部描述展开，再由尽头“返回”依次解决每步中剩余部分的问题 recursion(小规模); 
// 递去 solve; 
// 归来
} }

递归一般应用场景

问题的定义是按递归定义的（例如：Fibonacci函数，阶乘）；
问题的解法是递归的（例如，汉诺塔问题）；
数据结构是递归的（例如：链表、树等的操作）；

递归经典案例

✨求1-100的阶乘/和

//阶乘
function factorialize(n) {
  if (n == 1) //递归终止条件
      return 1; //简单情景
  return factorialize(n - 1) * n; //相同重复逻辑，缩小问题的规模
}
//和
function factorialize(n) {
  if (n == 1) return 1;
  return factorialize(n - 1) + n;
}

✨斐波拉契数列

1,1,2,3,5,8,13,21···
在数学上，斐波纳契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2，n∈N*）

/**
 * @description 经典递归法求解
 *
 * 斐波那契数列如下：
 *
 * 1,1,2,3,5,8,13,21,34,...
 *
 * 那么计算fib(5)时，需要计算1次fib(4),2次fib(3),3次fib(2)，调用了2次fib(1)，即
 *
 * fib(5) = fib(4) + fib(3)
 *
 * fib(4) = fib(3) + fib(2); fib(3) = fib(2) + fib(1)
 *
 * fib(3) = fib(2) + fib(1)
 */
function fibonacci(n) {
  if (n === 1 || n === 2)  //递归终止条件
      return 1; //简单情景
  return fibonacci(n - 1) + fibonacci(n - 2); //相同重复逻辑，缩小问题的规模
}

✨爬楼梯

假如楼梯有 n 个台阶，每次可以走 1 个或 2 个台阶，走完这 n 个台阶有几种走法?

/**
 * 假设有1个台阶，一步直接可以走完，有1种方法
 * 假设有2个台阶，先走1步在走1步或者直接走2步，共有2种方法
 * 假设有3个台阶
 * 方式一：先走1步，还剩2个台阶，由上可得两个台阶有2种走法
 * 方式二：先走2步，还剩1个台阶，由上可得一个台阶有1种走法
 * 所以三个台阶，共有3中方法
 *
 *归纳：climbStairs(n)=climbStairs(n-1)+climbStairs(n-2)
 */
function climbStairs(n) {
  if (n === 1) return 1;
  if (n === 2) return 2;
  return climbStairs(n - 1) + climbStairs(n - 2);
}

🧨汉诺塔

Title: 汉诺塔问题

Description:古代有一个梵塔，塔内有三个座A、B、C，A座上有64个盘子，盘子大小不等，大的在下，小的在上。

有一个和尚想把这64个盘子从A座移到C座，但每次只能允许移动一个盘子，并且在移动过程中，3个座上的盘子始终保持大盘在下，

小盘在上。在移动过程中可以利用B座。要求输入层数，运算后输出每步是如何移动的。

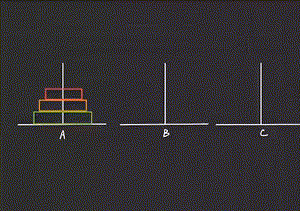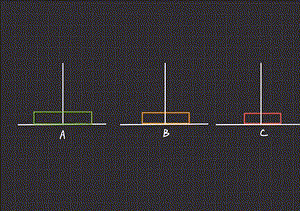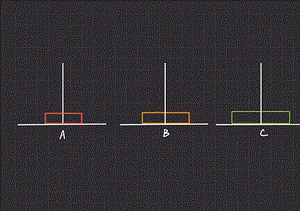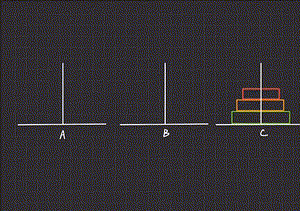
请添加图片描述

/**1个盘子：1号盘A->C  sum = 1
 * 2个盘子：
 * 第一次：1号盘 A -> B
 * 第二次：2号盘 A -> C
 * 第三次：1号盘 B -> C  sum = 3
 * 3个盘子：
 * 第一次：1号盘A->C
 * 第二次：2号盘A->B
 * 第三次：1号盘C->B
 * 第四次：3号盘A->C
 * 第五次：1号盘B->A
 * 第六次：2号盘B->C
 * 第七次：1号盘A->C  sum = 7
 * 归纳：移动次数为：2^n-1
 *
 * 把一堆圆盘从一个柱子移动另一根柱子，必要时使用辅助的柱子。可以把它分为三个子问题：
 * 首先，移动一对圆盘中较小的圆盘到辅助柱子上，从而露出下面较大的圆盘，
 * 其次，移动下面的圆盘到目标柱子上
 * 最后，将刚才较小的圆盘从辅助柱子上在移动到目标柱子上
 * 把三个步骤转化为简单数学问题：
 * 1.把n-1个盘子由A移到 B；
 * 2.把第n个盘子由 A移到 C；
 * 3.把n-1个盘子由B 移到 C；
 */
function HanoiTower(n, a, b, c) {
  if (n == 1) {
    console.log(a + "->" + c);
  } else {
    // 将n-1个盘子借助c从a移动到b
    HanoiTower(n - 1, a, c, b);
    console.log(a + "->" + b);
    // 将n-1个盘子借助a从b移动到c
    HanoiTower(n - 1, b, a, c);
  }
}
HanoiTower(3, "A", "B", "C");

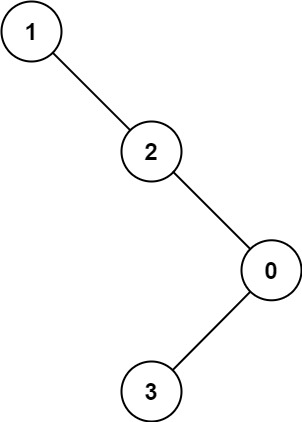
🎊二叉树的遍历

function getTreeDepth(tree) {
  // 树为空
  if (tree == null)
    // 递归终止条件
    return 0;

  let left = getTreeDepth(tree.left); // 递归求左子树深度，缩小问题的规模
  let right = getTreeDepth(tree.left); // 递归求右子树深度，缩小问题的规模

  return left > right ? left + 1 : right + 1;
}